6 Introduction to Bayesian statistics

本章では、ベイズ統計とマルコフ連鎖モンテカルロ法(MCMC)、integrated nested Laplace approximations(INLA)について解説を行う。

6.1 Why go Bayesian?

ベイズ統計を使うモチベーションとしてはいくつかある。

1. 事前に持っている知識を分析に取り入れるため。
   後に見るように、ベイズ統計では事前分布という形であらかじめ持っている知識を分析に組み込むことができる。

2. 頻度論的な統計学に対する批判から
   頻度論的な統計学とは、いわゆる帰無仮説検定(p値)に基づく統計学を指すが、p値や信頼区間などをめぐってはその解釈のしにくさや論理的な問題点に対してたびたび批判的な意見も投げかけられている(e.g., 岡田 and 大久保 2012; 松浦 2016)。

3. 複雑なモデルを使用するため
   時空間相関を考慮したGLMやGLMMなどの複雑なモデルは、通常の頻度論的な枠組みでは扱えないことが多い。ベイズ統計はこうした複雑なモデルを柔軟にモデリングすることを可能にする。

頻度論ではパラメータはある1つの真値を持つと考えられる一方で、ベイズ統計ではパラメータはある確率的な分布に従っているとされる(Kruschke 2014; 松浦 2016, ; 馬場 2019; McElreath 2020)。ベイズ統計を用いた分析では、データが得られた時のパラメータの分布(= 事後分布)を最終的に得る(\(P(\beta|D)\))。一方で、頻度論的な統計学ではパラ、エータがある値のときにデータが得られる確率(\(P(D|\beta)\))を計算する(= 尤度)。

6.2 General probability rules

まず確立の基本から確認していく。\(P(A)\)と\(P(B)\)をそれぞれ事象Aが生じる確率、事象Bが生じる確率とする。また、\(P(A \cap B)\)をAかつBである確率、\(P(A \cup B)\)をAまたはBである確率とする。このとき、

\[ P(A \cap B) = P(B \cap A) \]

である。また、AとBが独立であるときは以下のように書ける。
\[ P(A \cap B) = P(A) \times P(B) \]

一方、AとBが独立でないとき以下のように書ける。なお、\(P(A|B)\)は条件付き確率を表し、事象Bが生じたときに事象Aが生じる確率を表す。
\[ \begin{aligned} P(A \cap B) &= P(A|B) \times P(B)\\ P(A \cap B) &= P(B|A) \times P(A) \end{aligned} \tag{6.1} \]

よって、以下の式が導かれる。これを、ベイズの定理という。
\[ P(A|B) = \frac{P(B|A) \times P(A)}{P(B)} \tag{6.2} \]

6.3 The mean of a distribution

ある変数\(Y\)がパラメータ\(\mu\)のポワソン分布から得られるとき、\(Y\)の期待値は\(\mu\)である。このことは以下のように書ける。
\[ \begin{aligned} &Y \sim Poisson(\mu)\\ &E(Y) = \mu \end{aligned} \]

\(Y\)が離散的な値のとき、その期待値は以下のように書ける。なお、\(y\)は\(Y\)がとりうる全ての値を表す。よって、離散的な変数に関する確率分布(ポワソン分布、ベルヌーイ分布、二項分布、負の二項分布など)の期待値は以下の式で求められる。

\[ E(Y) = \sum_y y \times p(y) \tag{6.3} \]

ポワソン分布は\(p(y) = \frac{e^{-\mu} \times \mu^y}{y!}\)なので、式(6.3)は以下のように書ける。この式を計算すると右辺は\(\mu\)になる。
\[ E(Y) = \sum_{y =0} ^\infty y \times \frac{e^{-\mu} \times \mu^y}{y!} \tag{6.4} \]

もし変数\(Y\)が連続的な値の場合、その期待値は\(\int\)を用いて以下のように書ける。よって、連続的な変数に関する確率分布(正規分布、ガンマ分布、β分布など)の期待値は以下の式で求められる。
\[ E(Y) = \int _{-\infty} ^{\infty} y \times p(y) dy \tag{6.5} \]

6.4 Bayes theorem again

ベイズの定理(式(6.2))を用いて、データ(D)が得られたときにパラメータ\(\beta\)がとりうる確率の分布\(P(\beta|D)\)は以下のように書ける。

\[ P(\beta|D) = \frac{P(D|\beta) \times P(\beta)}{P(D)} \]

\(P(\beta|D)\)は、データが得られた時のパラメータ\(\beta\)の事後分布(posterior distribution)という。事後分布こそが、私たちがデータからパラメータを推定するときに求めたいものである。

\(P(D|\beta)\)はあるパラメータ\(\beta\)が与えられたときにデータが得られる確率であり、いわゆる尤度(likelihood)である。\(P(\beta)\)はデータが与えられていない状態でのパラメータ\(\beta\)が得られる確率分布で事前分布(prior distribution)と呼ばれる。

最後に、\(P(D)\)はデータが得られる確率で、事後分布の合計を1にするための役割を果たす。これは周辺尤度と言われ、通常計算することが難しいので省略されることが多い。このとき、式(6.2)は以下のように書ける。なお、\(\propto\)は左辺が右辺に比例することを表す。

\[ P(\beta|D) \propto P(D|\beta) \times P(\beta) \tag{6.6} \]

この式は、事後分布は尤度と事前分布の積に比例していることを示している。また、事後分布の期待値は式(6.5)から以下のように書ける。

\[ E(\beta|D) = \int_{-\infty} ^\infty \beta \times P(\beta|D) d\beta \]

次節以降では、事後分布とその期待値をどのように推定するかをみていく。

6.5 Conjugate priors

第2章で調べたように、ミサゴの卵の厚さが殺虫剤の崩壊産物(DDD)によって変わるかを検討するとする(Steidl et al. 1991)。第2と同様に以下のモデルを考える。

\[ \begin{aligned} &\mu_i = \beta_1 + DDD_i \times \beta_2 \\ &Thickness_i \sim N(\mu_i,\sigma^2) \end{aligned} \tag{6.7} \]

ここで、切片\(\beta_1\)と\(\sigma\)は分かっていると仮定し、事後分布\(P(\beta_2|D)\)を推定するとしよう。これを求めるには、式(6.6)で触れたように尤度\(P(D|\beta_2)\)と事前分布\(P(\beta_2)\)が必要である。

6.5.1 Likelihood function

\(P(D|\beta_2)\)はパラメータ\(\beta_2\)が与えられたときにデータDが得られる確率、すなわち尤度である。卵の殻の厚さは連続変数なので、ここではモデル式にあるようにデータが正規分布から得られていると仮定する。

このとき、尤度は式(6.7)より以下のように書ける¹。

\[ P(D|\beta_2) = \prod_i ^n \frac{1}{\sqrt{2 \pi \sigma^2}} exp\Bigl(-\frac{(Thickness_i - \beta_1 - DDD_i \times \beta_2)^2}{2\sigma^2}\Bigl) \tag{6.8} \]

頻度論的な統計学では、この尤度が最大になるようにパラメータ\(\beta_2\)を決定する。これは最尤推定法(maximum likelihood estimation)と呼ばれ、Rではglm関数などで実装されている。

6.5.2 Priors

続いて、事前分布\(P(\beta_2)\)について考える。これには、先行研究などの結果や生物学的知識などから予想される分布を適用することができる。事前分布としては、例えば以下のように正規分布を仮定することができる。

\[ \beta_2 \sim N(\beta_2^0, \sigma_0^2) \]

このとき、事前分布の確率密度関数は以下のように書ける。
\[ P(\beta_2) = \frac{1}{\sqrt{2 \pi \sigma_0^2}} exp\Bigl(-\frac{(\beta_2 - \beta_2^0)^2}{2\sigma_0^2}\Bigl) \tag{6.9} \]

6.5.3 Posterior distribution

式(6.8)の尤度と式(6.9)の事前分布から、事後分布は以下のように書ける。

\[ \begin{aligned} P(\beta_2|D) &\propto P(D|\beta_2) \times P(\beta_2) \\ &= \left[\prod_i ^n \frac{1}{\sqrt{2 \pi \sigma^2}} exp\Bigl(-\frac{(Thickness_i - \beta_1 - DDD_i \times \beta_2)^2}{2\sigma^2}\Bigl) \right] \times \left[ \frac{1}{\sqrt{2 \pi \sigma_0^2}} exp\Bigl(-\frac{(\beta_2 - \beta_2^0)^2}{2\sigma_0^2}\Bigl) \right] \end{aligned} \]

これは複雑な計算になるが、正規分布同士を掛け合わせているので事後分布も正規分布になる。このように、事前分布と事後分布の分布の関数形が同じになるようなとき、ベイズ統計ではこれらを共役分布という。このような分布の組み合わせはいくつかある(こちらを参照)。

これを計算すれば、事後分布やその期待値などを計算で求めることができる。なお、今回の場合は以下のような形になる。\(\hat{\beta_2}\)は\(\beta_2\)の最尤推定値である。

\[ \begin{aligned} &w = \frac{\sigma_0^2 \times \rm{something}}{\sigma_0^2 \times \rm{something} + \sigma^2}\\ &E(\beta_2|D) = \hat{\beta_2} \times w + (w-1) \times \beta_2^0 + \rm{Ugly \; stuff} \\ &var(\beta_2|D) = \sigma^2 \times \frac{w}{\rm{Ugly \; stuff}} \end{aligned} \tag{6.10} \]

6.5.4 Diffuse prior

多くの場合、私たちは事前分布に関する知識を持たない。そのとき、以下のように非常に広い分布を事前分布として指定することが多い。

\[ \beta_2 \sim N(0, 100) \Leftrightarrow \beta_2^0 = 0 \; and \; \sigma_0 = 100 \]

このとき、\(\beta_2\)はだいたい-200から200の間の値をとりうるということになる。このように広い範囲をもつ事前分布を無情報事前分布という。

無情報事前分布のとき(= \(\sigma_0\)が大きいとき)、式(6.10)の\(w\)は1に近づく。よって、\(P(\beta_2|D)\)の期待値は\(\hat{\beta_2}\)に近づき、頻度論的な統計学と同様に最尤推定値となる。

\[ P(\beta_2|D) \approx \hat{\beta_2} \]

実際に分布を書いてみるとこのことがよくわかる。図6.1は無情報事前分布のときの事前分布、尤度関数、事後分布を図示したものである。なお、\(\beta_1 = 51.7, \sigma = 5.17\)としている。無情報事前分布の場合、尤度関数と事後分布の形がほとんど同じになっていることが分かる。その結果、尤度関数における最尤推定値が事後分布の期待値とほぼ一致するのである。

beta2 <- seq(-20, 10, length.out = 100)
beta1 <- 51.7
sigma <- 5.17

## 尤度
likelihood <- vector()

for(i in 1:100){
likelihood[i] <- prod(dnorm(osp$THICK, mean = beta1 + beta2[i]*osp$DDD, sd = sigma))
}

## prior  
prior <- dnorm(beta2, mean = 0, sd = 100)

## 図示  
data.frame(beta2 = beta2,
           likelihood = likelihood,
           prior = prior) %>% 
  mutate(posterior = prior*likelihood) %>% 
  pivot_longer(2:4, names_to = "type", values_to = "probability") %>% 
  mutate(type = fct_relevel(type, "prior","likelihood","posterior")) %>% 
  ggplot(aes(x = beta2))+
  geom_line(aes(y = probability),
            linewidth = 1)+
  facet_rep_wrap(~type, repeat.tick.labels = TRUE, scales = "free_y")+
  theme_bw()+
  theme(aspect.ratio = 1,
        strip.background = element_blank(),
        strip.text = element_text(size = 13))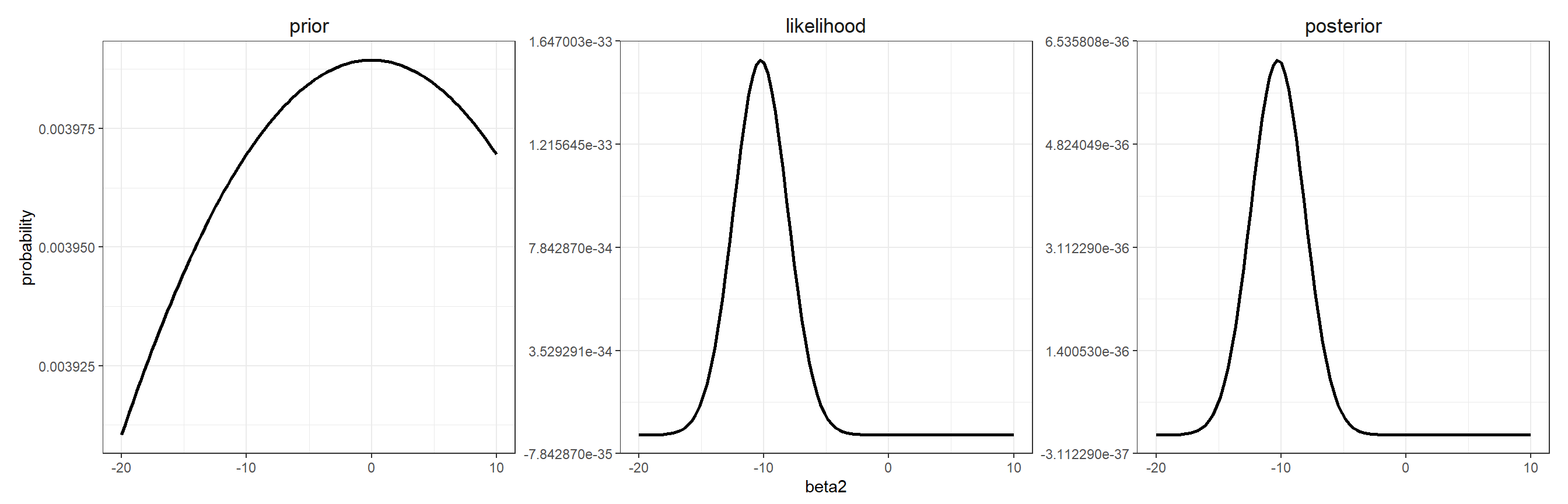

図6.1: Prior, likelihood, and posterior distribution.

6.5.5 Informative prior

一方で、パラメータ\(\beta_2\)に関してあらかじめ知識がある場合(e.g., 生態学的に考えて、ある範囲しか取り得ないなど)には、より狭い分布を持つ情報事前分布を用いることもできる。

例えば、以下のように非常に狭い事前分布を指定することもできる。
\[ \beta_2 \sim N(-18, 1) \Leftrightarrow \beta_2^0 = -18 \; and \; \sigma_0 = 1 \]

このとき、式(6.10)の\(w\)は0に近づいていく。その結果、事後分布の期待値は事前分布の期待値\(\beta_2^0\)に近づいていく。
\[ P(\beta_2|D) \approx \beta_2^0 \]

これも図示してみるとよくわかる。図6.2は情報事前分布のときの事前分布、尤度関数、事後分布を図示したものである。このとき事後分布と事前分布の分布の形がほとんど同じになっていることが分かる。その結果、事後分布の期待値が事前分布の期待値とほとんど同じになるのである。

beta2 <- seq(-23, 10, length.out = 100)
beta1 <- 51.7
sigma <- 5.17

## 尤度
likelihood <- vector()

for(i in 1:100){
likelihood[i] <- prod(dnorm(osp$THICK, mean = beta1 + beta2[i]*osp$DDD, sd = sigma))
}

## prior  
prior <- dnorm(beta2, mean = -18, sd = 1)

## 図示  
data.frame(beta2 = beta2,
           likelihood = likelihood,
           prior = prior) %>% 
  mutate(posterior = prior*likelihood) %>% 
  pivot_longer(2:4, names_to = "type", values_to = "probability") %>% 
  mutate(type = fct_relevel(type, "prior","likelihood","posterior")) %>% 
  ggplot(aes(x = beta2))+
  geom_line(aes(y = probability),
            linewidth = 1)+
  facet_rep_wrap(~type, repeat.tick.labels = TRUE, scales = "free_y")+
  theme_bw()+
  theme(aspect.ratio = 1,
        strip.background = element_blank(),
        strip.text = element_text(size = 13))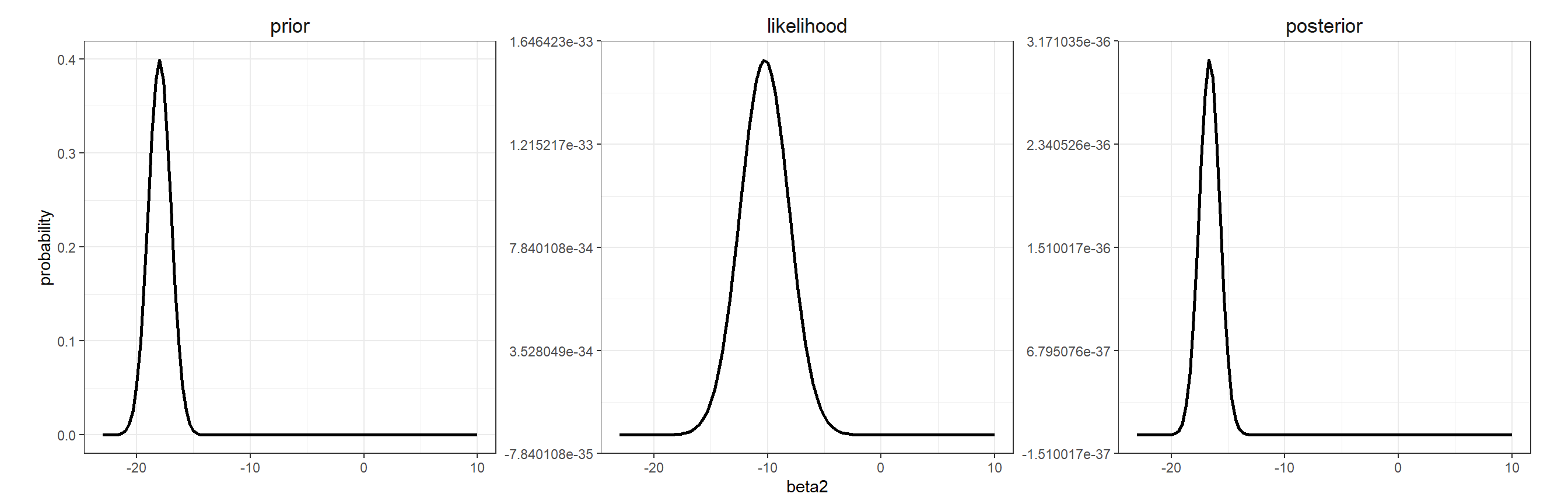

図6.2: Prior, likelihood, and posterior distribution.

以上のように、事前分布が情報を持たないほど(= 幅が広いほど)事後分布の期待値は最尤推定値に近づき、情報を持つほど(= 幅が狭いほど)事後分布の期待値は事前分布の期待値に近づく。

今回は\(\beta_2\)についてのみ事前分布を設定したが、実際の分析では全てのパラメータについて事前分布を設定する必要がある。回帰係数の事前分布としては、正規分布やt分布などが用いられることが多い。一方で、標準偏差\(\sigma\)は必ず0より大きい値をとるので、こうした分布は事前分布として不適切なことが多い。事前分布の選択については、こちらを参照。

Ntzoufras (2011) は、線形モデルの場合回帰係数\(\beta\)の事前分布が正規分布、\(\sigma\)の事前分布として逆ガンマ関数を用いると事前分布と事後分布が共役な分布になるとしている。\(\sigma^2\)の事前分布として逆ガンマ関数を用いるのは、\(\tau = 1/\sigma^2\)の事前分布としてガンマ関数を用いるのと同じである。このとき、\(\tau\)はprecision(精度)と呼ばれる。

本節では事後分布が手動で計算できるように共役な事前分布を用いた。しかし、これから見るような複雑なモデルでは手動で事後分布を求めることは困難になっていく。そこで用いられるのが次節で解説するMCMC法である。

6.6 Markov chain Monte Carlo simulation

6.6.1 underlying idea

マルコフ連鎖モンテカルロ(MCMC)法は、手動ではなくシミュレーションによって事後分布を推測する方法である。MCMCでは、全てのパラメータについて同時にこれを行う。例えば、卵の殻の厚さに関する分析(式(6.7))では、3つのパラメータ\(\bf{\theta} = (\beta_1, \beta_2, \sigma)\)について事後分布を同時に求める。

マルコフ連鎖とは、\(\bf{\theta}\)についてシミュレーションを行ったベクトル\(\theta^{(1)}, \theta^{(2)}, \theta^{(3)}, \dots, \theta^{(T)}\)を指し、\(\theta^{(t+1)}\)は\(\theta^{(t)}\)のみに依存する。数学的には以下のように書ける。

\[ f(\theta^{(t+1)}|\theta^{(t)}, \dots, \theta^{(1)}) = f(\theta^{(t+1)}|\theta^{(t)}) \]

MCMCでは各パラメータについて多くの(通常10000回以上)のシミュレーション値が得られる。これのシミュレーション値をヒストグラムにすると、それぞれのパラメータの事後分布に近似させることができることが数学的にわかっている。数学的な説明については、 Kruschke (2014) や McElreath (2020) などを参照。

6.6.2 Simple example of MCMC algorithm

ここでは、MCMCがどのように分布を推定できるのかを見るため、MCMC法の一種であるメトロポリスアルゴリズム(Metropolis algorithm)の特殊例について簡単に見ていく(McElreath 2020)。

10の島からなる諸島があるとする。それぞれの島は2つの島に隣接しており、全体で円になっている。各島は面積が異なり、それに比例して人口も異なる。面積と人口は1つめの島から順に2倍、3倍、…10倍になっている(つまり、1つめの島の大きさと人口が1だとすれば、10個目の島はそれぞれ10である)。さて、この諸島の王様は1週間ごとに島々を訪れるが、その際には隣接している島にしか移動できない。王様は各島を人口比率に応じて訪れたいが、訪問計画を長期的に策定するのは面倒である。そこで、彼の側近は以下の方法で島を訪れることを提案した。この方法に従えば、各島に訪れる頻度が人口比率に一致する。

1. 毎週王様はその島にとどまるか、隣接するいずれかの島に移動するかをコインを投げて決める。
   
2. もしコインが表なら、王様は時計回りに隣の島に移動することを考える。一方コインが裏なら、反時計回りに移動することを考える。ここで、提案された島をproposal islandとする。
   
3. 王様はporposal islandの大きさだけ(7つめの島にいるなら7個)貝殻を集める。また、現在いる島の大きさだけ同様に石を集める。
   
4. もし貝殻の数が石よりも多ければ、王様はproposal islandへ移動する。一方で石の数の方が多い場合、王様は集めた石から貝殻と同数の石を捨てる(例えば石が6つ、貝殻が4つなら、手元には\(6-4=2\)個の石が残る)。その後、残された石と貝殻をカバンに入れ、王様はランダムにそのうちの一つを引く。もしそれが貝殻ならばproposal islandに移動し、石ならば今いる島に留まる。
   
   

この方法は一見奇妙だが、長期間繰り返していくと非常にうまくいく。以下でシミュレーションしてみよう。

set.seed(9)

num_weeks <- 1e6
positions <- rep(0, num_weeks)
current <- 10

## アルゴリズムの記述
for(i in 1:num_weeks){
  ## 最初は島10からスタート
  positions[i] <- current
  proposal <- current + sample(c(-1,1), size=1)
  
  if(proposal <1)  proposal <- 10
  if(proposal >10) proposal <- 1
  
  prob_move <- proposal/current
  current <- ifelse(runif(1) < prob_move, proposal, current)
}

国王の動きを可視化してみる。

tibble(week = 1:1e6,
       island = positions) %>% 
  ggplot(aes(x=week, y = island))+
  geom_line(linewidth = 1/3)+
  geom_point()+
  coord_cartesian(xlim = c(0,500))+
  scale_y_continuous(breaks = seq(1,10,1))+
  theme_bw()+
  theme(aspect.ratio= 0.8)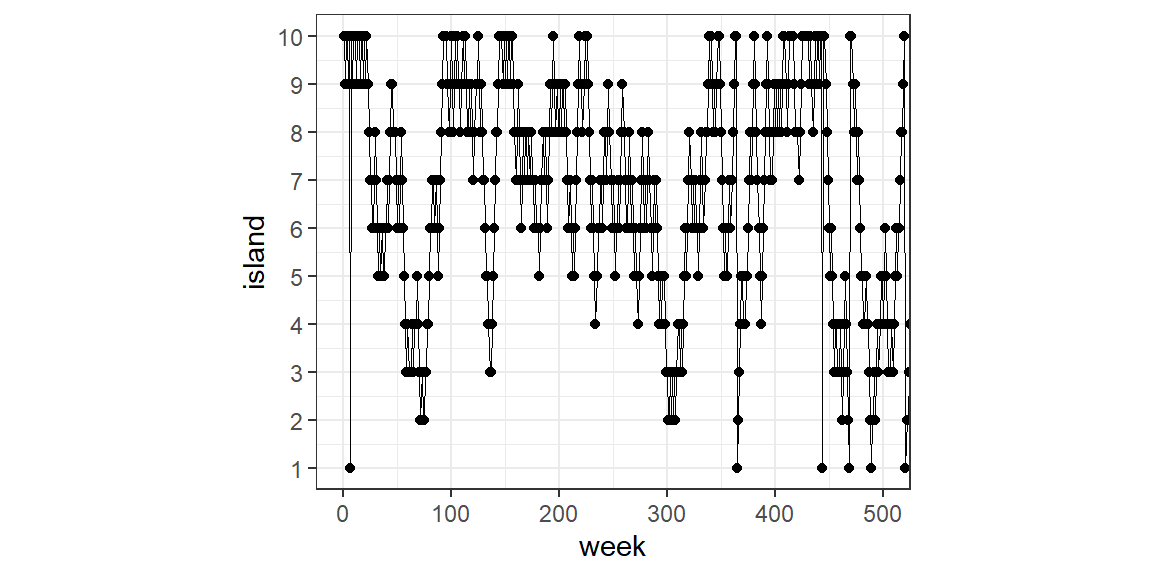

各島を訪れた回数を見てみると以下のようになり、人口に応じて訪れていることが分かる。

tibble(week = 1:1e6,
       island = positions) %>% 
  mutate(island = factor(island)) %>% 
  ggplot(aes(x=island))+
  geom_bar()+
  theme_bw()+
  theme(aspect.ratio = 0.9)+
  scale_y_continuous(breaks = seq(0,180000, 20000))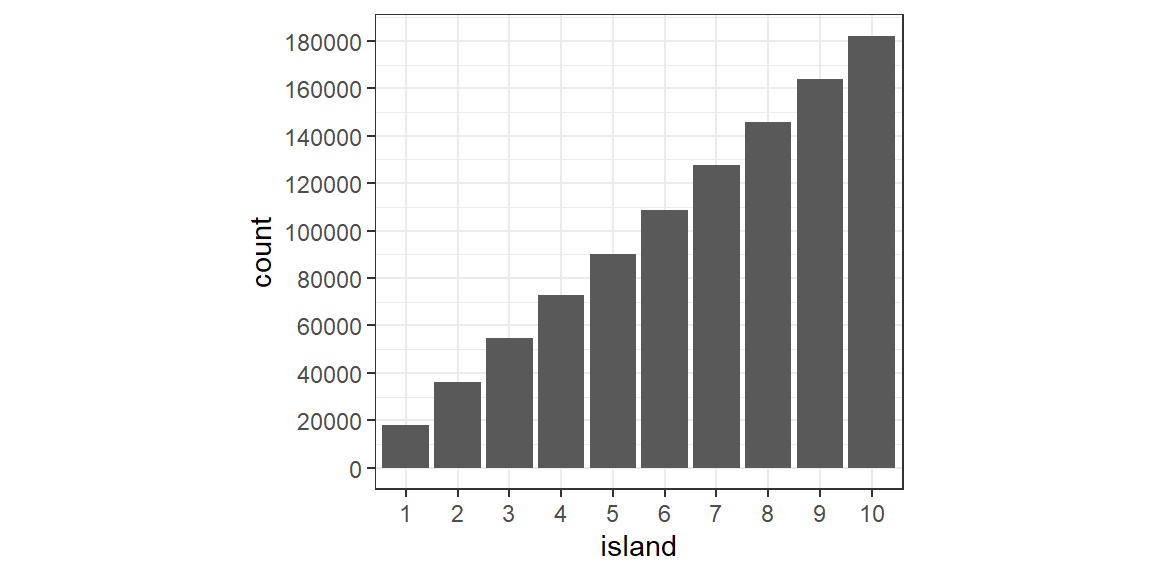

島を訪れている比率(prop)はおよそ人口通りになる。このアルゴリズムは、隣の島だけでなく全ての島への移動が可能であっても同様に機能する。

tibble(week = 1:1e6,
       island = positions) %>% 
  count(island) %>% 
  mutate(prop = n/n[1]) %>% 
  gt() %>% 
  fmt_number("prop",decimals=2) %>%
  tab_options(table.align='left')

island	n	prop
1	18142	1.00
2	36232	2.00
3	54787	3.02
4	72686	4.01
5	90272	4.98
6	108747	5.99
7	127527	7.03
8	145756	8.03
9	163703	9.02
10	182148	10.04

6.6.3 Methods in MCMC

MCMCにも様々なアルゴリズムがあり、それぞれの方法を実装するためのソフトウェアが開発されている。例えば、ギブスサンプリングと呼ばれる方法(Kruschke 2014; McElreath 2020)を実装するソフトウェアとしてJAGSやWinBUGSがある。また、ハミルトニアン・モンテカルロ法という方法を用いるソフトウェアとしては(Stan)[https://mc-stan.org/]がある(松浦 2016; 馬場 2019)。いずれもR上で実行することができる。

いずれを用いてもMCMCによるベイズ推定を行えるが、現在はStanが用いられることが多くなっている(松浦 2016)。この理由としては、WinBUGSやJAGSが使いにくい点や、開発があまり継続的には行われておらず、マニュアルや用例が充実していない点が挙げられる。また、Stanで用いられるハミルトニアン・モンテカルロ法はギブスサンプリングよりも複雑なモデルを扱え、またサンプリングも効率的に行える。そこで、本稿では以下Stanを用いてモデリングを行う²。RでStanを動かすには、rstanパッケージが必要である。`Stanのインストール方法や使用方法などは 松浦 (2016) や 馬場 (2019) を参照。

6.6.4 Flowchart for running a model in Stan

以下、Stanを用いてMCMCによって事後分布を推定する。分析には、第3で用いたデータを用いる。以下の線形モデルを考える。ひとまず、データの疑似反復については気にしない。

\[ \begin{aligned} pH_i &\sim N(0,\sigma^2)\\ \mu_i &= \beta_1 + \beta_2 \times SDI_i\\ \end{aligned} \tag{6.11} \]

6.6.4.1 Preparing the data for Stan

Stanで分析を行うためには、まずデータをlist形式で準備する必要がある。なお、説明変数\(SDI\)はモデルの収束をよくするために標準化する。

iph %>% 
  mutate(SDI.std = scale(SDI)) -> iph2

X <- model.matrix(~ 1 + SDI.std, data = iph2)

data_iph <- list(Y = iph2$pH,
                 X = X,
                 ##回帰係数の数
                 K = ncol(X),
                 ##データ数
                 N = nrow(iph2))

6.6.4.2 Decide model formulation and priors

パラメータの事前分布などを含めたモデルの詳細を決める。モデル式は式(6.11)の通りである。

パラメータ\(\beta\)の事前分布としては、以下の正規分布の無情報事前分布を用いることにする。

\[ \beta_1 \sim N(0,100^2) \;\; and \;\; \beta_2 \sim N(0,100^2) \]

\(\sigma\)の事前分布としては、0から20までの一様分布を用いる。
\[ \sigma \sim uniform(0,20) \]

6.6.4.3 Preparing stan file

最後に、ここまでのモデルの情報を記した以下のようなStanファイルを用意する。dataセクションにはデータの情報を、parameterセクションにはパラメータの情報を、modelセクションにはモデル式や事前分布に関する情報を入れる。

## // データ
## data {
##   int N;
##   int K; 
##   vector[N] Y;
##   matrix[N, K] X;
## }
## 
## // パラメータ  
## parameters {
##   vector[K] beta;
##   real<lower=0> sigma;
## }
## 
## // モデル式、事前分布  
## model {
##   vector[N] mu = X*beta;
##   Y ~ normal(mu, sigma);
##   
##   //βの事前分布
##   for(i in 1:K){
##     beta[i] ~ normal(0, 100);
##   }
##   
##   //σの事前分布  
##   sigma ~ uniform(0,20);
## }

6.6.4.4 Initial values

パラメータのMCMCの初期値を定める場合には、指定することができる。今回は、\(\beta_1, \beta_2\)の初期値については平均0、標準偏差10の正規分布から、\(\sigma\)の初期値は0から20までの一様分布から得られるとした。

K <- ncol(X)
inits <- function() {
  list(beta = rnorm(K, 0, 10),
  sigma = runif(1, 0,20))
}

6.6.5 Running model in Stan

それでは、実際にStanでモデルを回してみよう。

まず、rstanパッケージを読み込む。バックエンドとして、cmdstanrパッケージを用いる。

library(rstan)
library(cmdstanr)
library(posterior)

以下のオプションを実行すると、実行時間が短くなる。

rstan_options(auto_write = TRUE) 
options(mc.cores = parallel::detectCores())

MCMCによるパラメータの推定は以下のように行う。

• file: stanファイル
  
• data: リスト化したデータ
  
• init: 初期値
  
• chains: 何セットの乱数生成(MCMC)を行うか
  
• iter_warmup: チューニングを行う回数。切り捨てる。
  
• iter_sampling: warmup期間を含む各chainの乱数生成回数。
  
• thin: 何回に一回の乱数を用いるか

今回の場合、4つのchainで繰り返し数(iter_sampling)が50000、間引き期間(thin)が10なので、\((50000)/10 \times 4 = 20000\)個の乱数がパラメータごとに得られる。

mod <- cmdstan_model("stanfile/lm-iph.stan")

m7_1 <- mod$sample(data = data_iph,
                   init = inits,
                   seed = 1234,
                   ## 何回に一回のデータを使うか
                   thin = 10,
                   ## 最初の何回を捨てるか 
                   iter_warmup = 5000,
                   ## 乱数生成の繰り返し数(warmupを除く)  
                   iter_sampling = 50000,
                   ## chainの数 
                   chains = 4)

6.6.6 Assess mixing

結果を見る前に、まず信頼できるMCMCサンプルが得られたかを確認する必要がある。

得られたMCMCサンプルは以下のように取り出せる。

draw_m7_1 <- m7_1$draws(format = "df")

datatable(draw_m7_1)

まずは、MCMCが収束しているかを確認する。視覚的には、横軸に繰り返し(iteration)数をとり、chainごとにその遷移を確認する。全てのchainがまじりあっていれば問題がない。図を見る限りは問題がなさそう。

mcmc_trace(draw_m7_1)

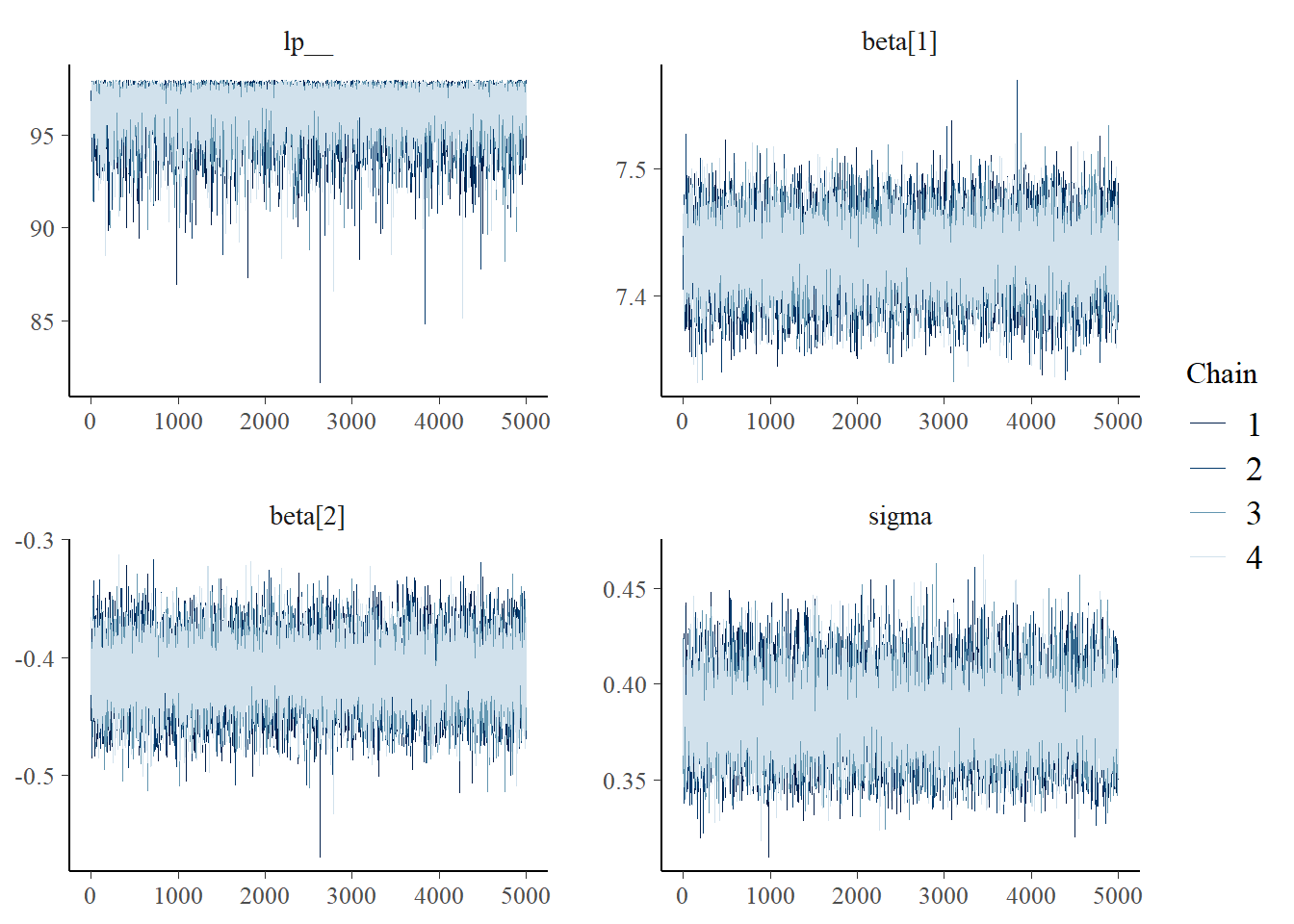
また、収束をチェックするための指標としては、\(\hat{R}\)と有向サンプルサイズ数がある。前者は1.1未満であれば、後者は100くらいあれば問題ないとされている(松浦 2016)。今回は問題なさそう(rhatとess_bulkをチェックする)。

m7_1$summary(NULL, c("Rhat", "ess_bulk"))

いよいよ、結果を確認する。まずは、事後分布の代表値なども一緒にチェックする。以下には、事後分布の平均(mean)、中央値(median)、標準偏差(sd)、中央値絶対偏差(mad)、2.5パーセンタイル(q2.5)、97.5パーセンタイル(q97.5)を示した。2.5パーセンタイルと97.5パーセンタイルの間の範囲を95%確信区間(credible interval)という。これらは全てMCMCで生成された乱数から計算されている。

\(\beta_2\)の95%確信区間は\([-0.463, -0.361]\)で0を含まない。これは、\(\beta_2\)が95%の確率でこの区間の値をとるということを表す。このことから、SDIはpHと強く関連しているといえそうだ。

m7_1$summary(variables = NULL,
             c("mean", "median","sd", "mad"),
             quantiles = ~posterior::quantile2(., probs = c(.0275, .975))) -> result7_1

result7_1

最後に、事後分布を実際に図示する。

mcmc_hist(draw_m7_1,
          pars = c("beta[1]","beta[2]", "sigma"))+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(y = "Frequencies")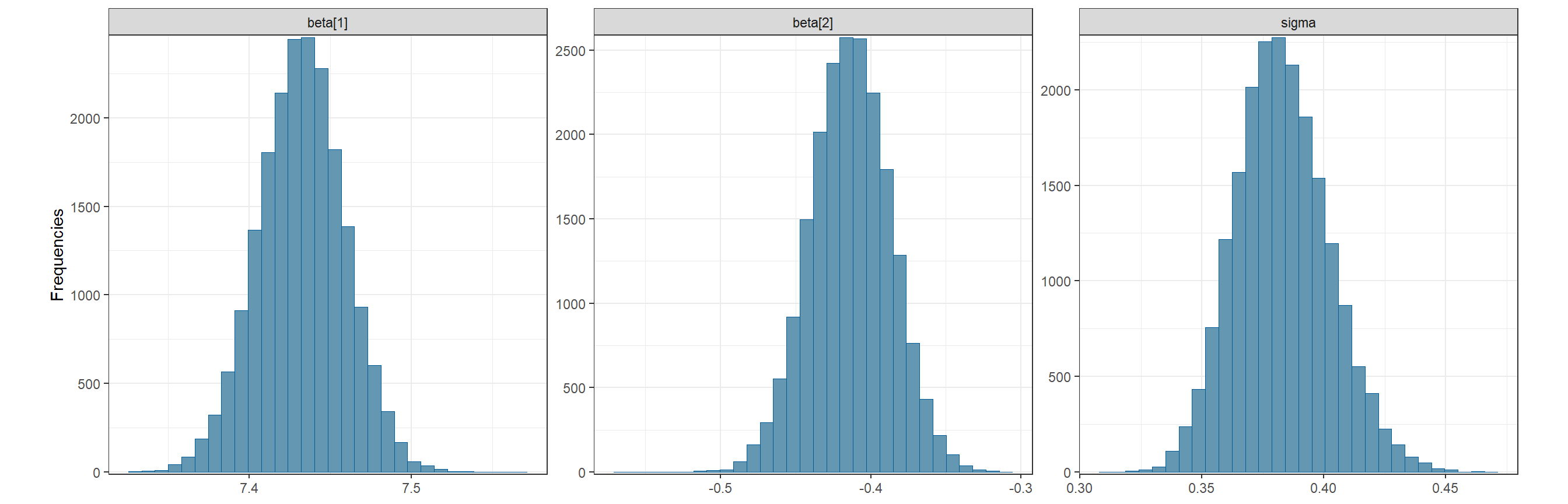

6.7 Integrated nested Laplace approximation

Stanでは、前節と同様にして様々なモデルを実装することができる。しかし、時空間相関を考慮するなど複雑なモデルになると、MCMCでは時間がかかりすぎる場合やモデルが収束しない場合が出てくる。本節では、MCMCによらず事後分布を近似させる手法である integrated nested Laplace approximation(INLA)について学ぶ。INLAはMCMCよりもはるかに拘束に、かつ精度高く事後分布を推定することができる。しかし、以下の数学的説明はかなり高度なので、全てを理解する必要はない。

6.7.1 Joint posterior distribution

ここまでと同様に、ミサゴの卵の厚さが殺虫剤の崩壊産物(DDD)によって変わるかを検討するとする(Steidl et al. 1991)。同様に以下のモデルを考える。 　

\[ \begin{aligned} &\mu_i = \beta_1 + DDD_i \times \beta_2 \\ &Thickness_i \sim N(\mu_i,\sigma^2) \end{aligned} \tag{6.12} \]

式(6.12)には3つのパラメータ(\(\beta_1, \beta_2, \sigma\))があるが、\(\sigma\)のようなパラメータはハイパーパラメータと呼ばれる。ハイパーパラメータには、負の二項分布モデルなどの分散パラメータや、ランダム効果(混合)モデルのランダム切片の分散パラメータ、時空間相関を考慮したモデルにおけるパラメータ(\(\phi, \kappa\)など)がある。

ベイズの定理から、以下の式が導ける。
\[ \begin{aligned} P(\beta_1, \beta_2, \sigma|D) &= \frac{P(D|\beta_1, \beta_2, \sigma) \times P(\beta_1, \beta_2, \sigma)}{P(D)}\\ &\propto P(D|\beta_1, \beta_2, \sigma) \times P(\beta_1, \beta_2, \sigma) \end{aligned} \tag{6.13} \]

\(P(\beta_1, \beta_2, \sigma|D)\)はデータ(D)が与えられた時のパラメータの同時分布である。\(P(D|\beta_1, \beta_2, \sigma)\)はデータの尤度、\(P(\beta_1, \beta_2, \sigma))\)はパラメータの事前分布である。\(pH\)が正の連続値であると考えると、正規分布かガンマ分布を用いて書くことができるだろう。\(\beta_1, \beta_2\)は全ての値が取れるのに対して\(\sigma\)は0より大きい値しか取れないので、これらにすべて同じ事前分布を仮定することはできない。そのため、事前分布は\(\beta_1, \beta_2\)のためのものと、\(\sigma\)のためのものの2種類を含むように書き直す必要がある。

式(6.1)より、式(6.13)は\(P(\beta_1, \beta_2, \sigma))\)を変形して以下のように書き直せる。これにより、事前分布を2つの要素に分けることができた。

\[ \begin{aligned} P(\beta_1, \beta_2, \sigma)|D) &\propto P(D|\beta_1, \beta_2, \sigma) \times P(\beta_1, \beta_2, \sigma) \\ &= P(D|\beta_1, \beta_2, \sigma) \times P(\beta_1, \beta_2| \sigma) \times P(\sigma) \end{aligned} \tag{6.14} \]

\(\beta_s\)の事前分布\(P(\beta_1, \beta_2| \sigma)\)は少しトリッキーだが、互いに独立に多変量正規分布から得られていると仮定すればうまくいくことが多い。

6.7.2 Marginal distributions

MCMCでは各パラメータの事後分布\(P(\beta_1|D), P(\beta_2|D), P(\sigma|D)\)が得られた。これらは周辺分布(marginal distribution)といい、同時事後確率\(P(\beta_1, \beta_2, \sigma)|D)\)を得たわけではなかった。

同時分布と周辺分布の違いを説明するため、ミヤコドリ(Haematopus palliates)を対象とした研究のデータを用いる。この研究では、3か所で12月から1月にミヤコドリによって食べられた二枚貝の長さが記録されている。ミヤコドリは、採食技術によってhammererまたはstabberに分類された。リサーチクエスチョンは、採食技術のタイプによって貝の長さが変わるかである。

oc <- read_delim("data/Oystercatcher.txt") 

datatable(oc,
          options = list(scrollX = 20),
          filter = "top")

下表(表6.1)は、hammererによって割られた二枚貝のサイズ(Large or Small)を場所ごとにまとめたものである。

oc %>% 
  filter(FeedingType == "Hammerers") %>% 
  mutate(shell_size = ifelse(ShellLength >= 2, "Large","Small")) %>% 
  group_by(shell_size, FeedingPlot) %>% 
  summarise(N = n()) %>% 
  rename("Shell size" = 1, "Feeding site" = 2) %>% 
  pivot_wider(names_from = "Feeding site", values_from = N) %>% 
  ungroup() %>% 
  mutate(Total = A + B + C) -> sum_oc

sum_oc %>% 
  bind_rows(summarise(., across(where(is.numeric), sum),
                                   across(where(is.character), ~'Total'))) %>% 
　kable(booktabs = TRUE, align = c("l", rep("c",5)),
　      caption = "Number  of  clams  eaten  by  hammering  oystercatchers  per  shell size (small versus large) and feeding site.") %>% 
  add_header_above(c(" " = 1, "Feed place" = 4)) %>% 
  kable_styling(full_width = FALSE)

表6.1: Number of clams eaten by hammering oystercatchers per shell size (small versus large) and feeding site.

	Feed place
Shell size	A	B	C	Total
Large	45	29	36	110
Small	15	16	24	55
Total	60	45	60	165

これを割合データに直したのが表6.2である。

sum_oc %>% 
  bind_rows(summarise(., across(where(is.numeric), sum),
                                   across(where(is.character), ~'Total'))) %>% 
  mutate_if(is.numeric, .funs = ~./165) %>% 
  mutate_if(is.numeric, ~sprintf("%.3f", .)) %>% 
  kable(booktabs = TRUE, align = c("l", rep("c",5)),
　      caption = "Proportions  of  clams  eaten by  hammering  oystercatchers  per shell size (small versus large) and feeding site.") %>% 
  add_header_above(c(" " = 1, "Feed place" = 4)) %>% 
  kable_styling(full_width = FALSE)

表6.2: Proportions of clams eaten by hammering oystercatchers per shell size (small versus large) and feeding site.

	Feed place
Shell size	A	B	C	Total
Large	0.273	0.176	0.218	0.667
Small	0.091	0.097	0.145	0.333
Total	0.364	0.273	0.364	1.000

このとき、\(P(\rm{shell \; size} \; \mathbf{and} \rm{\;Feed \; place})\)が同時確率であり、中の6つのセルの値である。

一方、\(P(\rm{Feed \;place})\)と\(P(\rm{Shell \; size})\)が周辺確率である。これらは、それぞれ一番下の行と一番右の列の値である。

\[ \begin{aligned} &P(\rm{Feed \;place} = A) = 0.273 + 0.091 = 0.364 \\ &P(\rm{Feed \;place} = B) = 0.176 + 0.097 = 0.273 \\ &P(\rm{Feed \;place} = C) = 0.218 + 0.145 = 0.364 \\ \\ &P(\rm{Shell \; size = Large}) = 0.273 + 0.16 + 0.218 = 0.667 \\ &P(\rm{Shell \; size = Small}) = 0.091 + 0.097 + 0.145 = 0.333 \end{aligned} \]

より一般的に、変数が離散的なとき周辺確率は以下のように書ける。
\[ P(X = x) = \sum_y P(X = x \; \rm{and} \; Y = y) \]

変数が連続的なとき、以下のように書ける。
\[ P(X = x) = \int_y P(X = x \; \rm{and} \; Y = y) dy \tag{6.15} \]

このように、複数の確率変数の同時分布(確率)から周辺分布(確率)を計算することを周辺化という(馬場 2019)。周辺事後分布\(P(\beta_1|D), P(\beta_2|D), P(\sigma|D)\)を求めるときも、同じように積分を用いて周辺化を行う。

6.7.3 Back to high school

それでは、積分とは何だろうか。例えば、図6.3Aの塗りつぶされた場所の面積を求めたいとする(なお、曲線は\(f(x) = -2x^2 + 8\))。いうまでもなく\(\int_0 ^1 f(x) dx\)という積分計算を行えばこれを求めることができるが、積分を用いずにこれを近似することはできるだろうか?

よく用いられるのは、面積を求めたいエリアの\(x\)軸(その範囲を\(x_0\)とする)をN等分したのち、面積を求めたいエリアを幅\(x_0/N\)、高さ\(f(x)\)の長方形N個で埋め尽くし、その面積の合計を近似値として求める方法である。例えば、図6.3Bは面積を求めたいエリアを5等分した場合である。Nを大きくすればするほど近似値は実際の面積に近づいていく(図6.3C)。これを区分求積法という。INLAでも、積分計算に区分求積法のような方法を用いることで近似を行う。

X <- seq(-0.5, 2, length = 100)
Y <- -2*X^2 + 8  

data.frame(X = X,
           Y = Y) %>% 
  ggplot(aes(x = X, y = Y))+
  geom_area(aes(x = ifelse(X>=0 & X <= 1 , X, 0)),
            fill = "lightblue")+
  geom_line(linewidth = 1)+
  theme_bw()+
  theme(aspect.ratio = 1)+
  coord_cartesian(ylim = c(0.35,8))+
  labs(title = "A") -> p1

int <- data.frame(X = seq(0,0.8,0.2)) %>% 
  mutate(Y = -2*X^2 + 8) 

data.frame(X = X,
           Y = Y) %>% 
  ggplot(aes(x = X, y = Y))+
  geom_area(aes(x = ifelse(X>=0 & X <= 1 , X, 0)),
            fill = "lightblue")+
  geom_line(linewidth = 1)+
  geom_col(data = int,
           color = "black",
           alpha = 0,
           linewidth = 0.3,
           width = 0.2,
           position = position_nudge(x = 0.1)) +
  theme_bw()+
  theme(aspect.ratio = 1)+
  coord_cartesian(ylim = c(0.35,8))+
  labs(title = "B")-> p2

int2 <- data.frame(X = seq(0,0.9,0.1)) %>% 
  mutate(Y = -2*X^2 + 8) 

data.frame(X = X,
           Y = Y) %>% 
  ggplot(aes(x = X, y = Y))+
  geom_area(aes(x = ifelse(X>=0 & X <= 1 , X, 0)),
            fill = "lightblue")+
  geom_line(linewidth = 1)+
  geom_col(data = int2,
           color = "black",
           alpha = 0,
           linewidth = 0.2,
           width = 0.1,
           position = position_nudge(x = 0.05)) +
  theme_bw()+
  theme(aspect.ratio = 1)+
  coord_cartesian(ylim = c(0.35,8))+
  labs(title = "C")-> p3

p1 + p2 + p3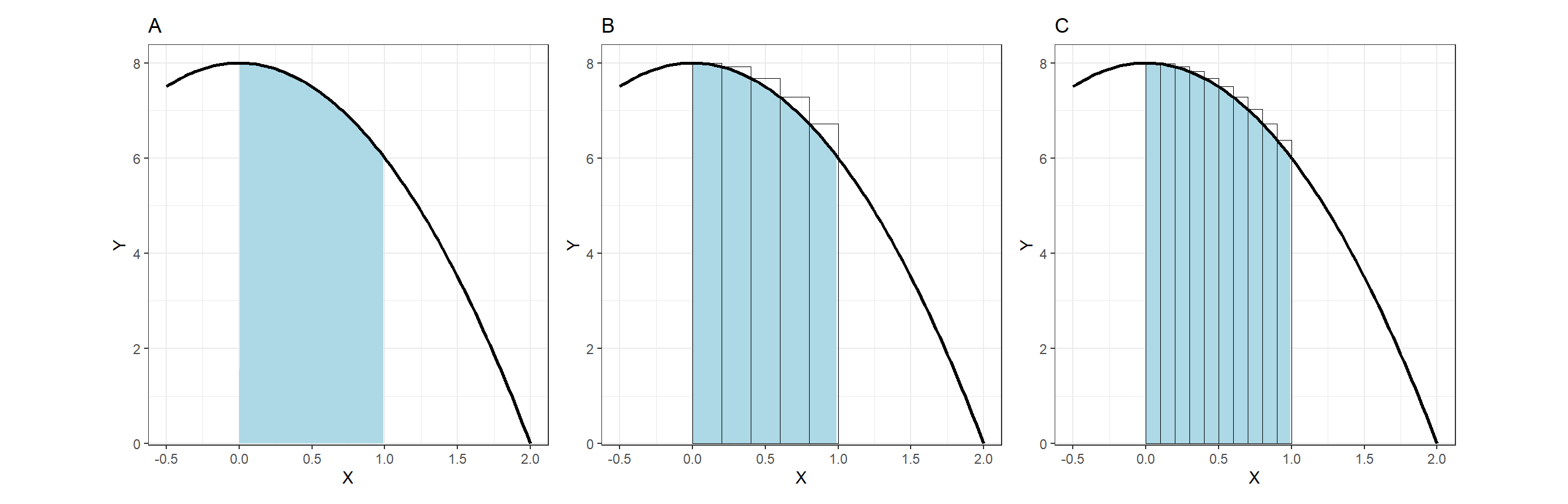

図6.3: How integrals work.

実際の分析ではより複雑な関数を積分しなくてはいけないので、実際には積分を行うことが非常に難しいこともある。INLAではラプラス近似(テイラー展開を用いて関数を近似する方法)を用いて\(f(x)\)を近似することで、複雑な積分計算を可能にする。もう少し詳しい説明については、こちらなどを参照。

6.7.4 INLA

式(6.15)より、\(\beta_1, \beta_2\)の事後分布は以下のように書ける。

\[ \begin{aligned} &P(\beta_1|D) = \int P(\beta_1, \sigma|D)d\sigma \\ &P(\beta_2|D) = \int P(\beta_2, \sigma|D)d\sigma \end{aligned} \tag{6.16} \]

混合モデルなど、ハイパーパラメータが2つあるときには、これらの事後分布を以下のように求める。
\[ P(\sigma_1|D) = \int(\sigma_1, \sigma_2|D)d\sigma_1 \\ P(\sigma_2|D) = \int(\sigma_1, \sigma_2|D)d\sigma_2 \]

ひとまず、今回はハイパーパラメータが$$1つの場合を考える。このとき、式(6.16)は条件付き確率の書き換えルール(式(6.1))を用いて以下のように書き換えられる³。

\[ \begin{aligned} &P(\beta_1|D) = \int P(\beta_1|\sigma,D) \times P(\sigma|D) d\sigma \\ &P(\beta_2|D) = \int P(\beta_2|\sigma,D) \times P(\sigma|D) d\sigma \end{aligned} \]

よって、事後分布を求めるには2つの要素を計算できれば良い。\(P(\sigma|D)\)はハイパーパラメータが1つなので簡単に求められる。もし、ハイパーパラメータが2つ以上のときはこれをさらに簡単な要素に分解する。\(P(\beta_1|\sigma,D)\)の計算にはいくつかの方法があるが、INLAではラプラス近似を用いてこれを求める。

6.8 Examples using R-INLA

以下では、INLAパッケージを用いて式(6.12)の線形モデルを実行する。INLAのコードは非常にシンプルで、他の関数(lm、glm)と同じようにできる。

m7_2 <- inla(pH ~ SDI.std,
             data = iph2,
             family = "gaussian")

違う点は、分布をfamily =で必ず指定しなければいけない点である。INLAでは非常に多くの分布を扱える。

names(inla.models()$likelihood) 

##  [1] "poisson"                       "xpoisson"                     
##  [3] "cenpoisson"                    "cenpoisson2"                  
##  [5] "gpoisson"                      "poisson.special1"             
##  [7] "0poisson"                      "0poissonS"                    
##  [9] "bell"                          "0binomial"                    
## [11] "0binomialS"                    "binomial"                     
## [13] "xbinomial"                     "pom"                          
## [15] "bgev"                          "gamma"                        
## [17] "gammasurv"                     "gammajw"                      
## [19] "gammajwsurv"                   "gammacount"                   
## [21] "qkumar"                        "qloglogistic"                 
## [23] "qloglogisticsurv"              "beta"                         
## [25] "betabinomial"                  "betabinomialna"               
## [27] "cbinomial"                     "nbinomial"                    
## [29] "nbinomial2"                    "cennbinomial2"                
## [31] "simplex"                       "gaussian"                     
## [33] "gaussianjw"                    "agaussian"                    
## [35] "circularnormal"                "wrappedcauchy"                
## [37] "iidgamma"                      "iidlogitbeta"                 
## [39] "loggammafrailty"               "logistic"                     
## [41] "sn"                            "gev"                          
## [43] "lognormal"                     "lognormalsurv"                
## [45] "exponential"                   "exponentialsurv"              
## [47] "coxph"                         "weibull"                      
## [49] "weibullsurv"                   "loglogistic"                  
## [51] "loglogisticsurv"               "stochvol"                     
## [53] "stochvolsn"                    "stochvolt"                    
## [55] "stochvolnig"                   "zeroinflatedpoisson0"         
## [57] "zeroinflatedpoisson1"          "zeroinflatedpoisson2"         
## [59] "zeroinflatedcenpoisson0"       "zeroinflatedcenpoisson1"      
## [61] "zeroinflatedbetabinomial0"     "zeroinflatedbetabinomial1"    
## [63] "zeroinflatedbinomial0"         "zeroinflatedbinomial1"        
## [65] "zeroinflatedbinomial2"         "zeroninflatedbinomial2"       
## [67] "zeroninflatedbinomial3"        "zeroinflatedbetabinomial2"    
## [69] "zeroinflatednbinomial0"        "zeroinflatednbinomial1"       
## [71] "zeroinflatednbinomial1strata2" "zeroinflatednbinomial1strata3"
## [73] "zeroinflatednbinomial2"        "t"                            
## [75] "tstrata"                       "nmix"                         
## [77] "nmixnb"                        "gp"                           
## [79] "dgp"                           "logperiodogram"               
## [81] "tweedie"                       "fmri"                         
## [83] "fmrisurv"                      "gompertz"                     
## [85] "gompertzsurv"

6.8.1 Posterior summary

推定された事後分布の要約は以下の通り。事後分布の平均、sd、パーセンタイル値などの情報が出る。結果はほぼMCMCのときと変わらない。

summary(m7_2)

## 
## Call:
##    c("inla.core(formula = formula, family = family, contrasts = contrasts, 
##    ", " data = data, quantiles = quantiles, E = E, offset = offset, ", " 
##    scale = scale, weights = weights, Ntrials = Ntrials, strata = strata, 
##    ", " lp.scale = lp.scale, link.covariates = link.covariates, verbose = 
##    verbose, ", " lincomb = lincomb, selection = selection, control.compute 
##    = control.compute, ", " control.predictor = control.predictor, 
##    control.family = control.family, ", " control.inla = control.inla, 
##    control.fixed = control.fixed, ", " control.mode = control.mode, 
##    control.expert = control.expert, ", " control.hazard = control.hazard, 
##    control.lincomb = control.lincomb, ", " control.update = 
##    control.update, control.lp.scale = control.lp.scale, ", " 
##    control.pardiso = control.pardiso, only.hyperparam = only.hyperparam, 
##    ", " inla.call = inla.call, inla.arg = inla.arg, num.threads = 
##    num.threads, ", " blas.num.threads = blas.num.threads, keep = keep, 
##    working.directory = working.directory, ", " silent = silent, inla.mode 
##    = inla.mode, safe = FALSE, debug = debug, ", " .parent.frame = 
##    .parent.frame)") 
## Time used:
##     Pre = 0.738, Running = 0.435, Post = 0.0589, Total = 1.23 
## Fixed effects:
##               mean    sd 0.025quant 0.5quant 0.975quant   mode kld
## (Intercept)  7.432 0.026      7.381    7.432      7.484  7.432   0
## SDI.std     -0.414 0.026     -0.465   -0.414     -0.362 -0.414   0
## 
## Model hyperparameters:
##                                         mean    sd 0.025quant 0.5quant
## Precision for the Gaussian observations 6.97 0.681       5.71     6.95
##                                         0.975quant mode
## Precision for the Gaussian observations       8.37 6.91
## 
## Marginal log-Likelihood:  -113.24 
##  is computed 
## Posterior summaries for the linear predictor and the fitted values are computed
## (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

ハイパーパラメータ以外の結果を知りたい場合は以下のようにしてみることができる。

m7_2$summary.fixed %>% 
  select(mean, sd, "0.025quant", "0.975quant")

事後分布の平均を用いた予測値や残差は以下のように計算できる。

X <- model.matrix(~ 1 + SDI.std, data = iph2)
beta <- m7_2$summary.fixed %>% select("mean") %>% .[,1]

fit7_2 <- X %*% beta
e7_2 <- iph$pH - fit7_2

自分で計算しなくても、INLAでcontrol.predictorオプションを加えれば自動で計算を行ってくれる。95%確信区間の計算も行ってくれるようだ。

m7_2 <- inla(pH ~ SDI.std, data = iph2,
             family = "gaussian",
             control.predictor = list(compute = TRUE),
             control.compute = list(config = TRUE))

fit7_2 <- m7_2$summary.fitted.values

datatable(fit7_2)

ハイパーパラメータは以下のように求めることができる。INLAパッケージでは標準偏差ではなくprecision(\(\tau = 1/\sigma^2\)が推定される。

m7_2$summary.hyperpar

6.8.2 Posterior marginal distributions

ある特定のパラメータに関する事後分布は事後周辺分布(posterior marginal distribution)と呼ばれる⁴。以後、これを事後分布と呼ぶ(先ほどの節の結果で示されたのも事後周辺分布の要約である)。先ほど推定したモデルでは3つのパラメータ(\(\beta_1, \beta_2, 1 / \sigma^2\))があった。これらの事後分布は以下のように抽出できる。

pmbeta1 <- m7_2$marginals.fixed$`(Intercept)`
pmbeta2 <- m7_2$marginals.fixed$SDI.std
pmtau <- m7_2$marginals.hyperpar$`Precision for the Gaussian observations`

INLAには事後周辺分布の確信区間などの要約統計量を算出するための関数が装備されている。例えば、95%確信区間と中央値は以下のように求められる。

inla.qmarginal(p = c(0.025, 0.5, 0.975), pmbeta1)

## [1] 7.380707 7.432135 7.483562

inla.zmarginalでは、自動的に要約統計量を算出してくれる。

inla.zmarginal(pmbeta2)

## Mean            -0.413666 
## Stdev           0.0262696 
## Quantile  0.025 -0.465272 
## Quantile  0.25  -0.431393 
## Quantile  0.5   -0.413722 
## Quantile  0.75  -0.39605 
## Quantile  0.975 -0.362171

また、最高密度区間(highest posterior density)⁵は以下のように求められる。

inla.hpdmarginal(0.95, pmbeta2)

##                   low       high
## level:0.95 -0.4652722 -0.3621714

precision\(\tau\)は容易に\(\sigma\)に変換できる。

pm.sigma <- inla.tmarginal(function(x) sqrt(1/x), pmtau)

事後分布はこれらを用いて容易に作図できる。

## beta1 
pmbeta1 %>% 
  data.frame() %>% 
  ggplot(aes(x = x, y = y))+
  geom_area(fill = "lightblue")+
  geom_line()+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(x = expression(beta[1]),
       y = expression(paste("P( ", beta[1] ," | Data)"))) -> p1

## beta2
pmbeta2 %>% 
  data.frame() %>% 
  ggplot(aes(x = x, y = y))+
  geom_area(fill = "lightblue")+
  geom_line()+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(x = expression(beta[2]),
       y = expression(paste("P( ", beta[2] ," | Data)"))) -> p2

## tau
pmtau %>% 
  data.frame() %>% 
  ggplot(aes(x = x, y = y))+
  geom_area(fill = "lightblue")+
  geom_line()+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(x = expression(tau),
       y = expression(paste("P( ", tau ," | Data)"))) -> p3

## sigma
pmtau %>% 
  data.frame() %>% 
  ggplot(aes(x = x, y = y))+
  geom_area(fill = "lightblue")+
  geom_line()+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(x = expression(sigma),
       y = expression(paste("P( ", sigma ," | Data)"))) -> p4

p1 + p2 + p3 + p4 + plot_layout(ncol = 2)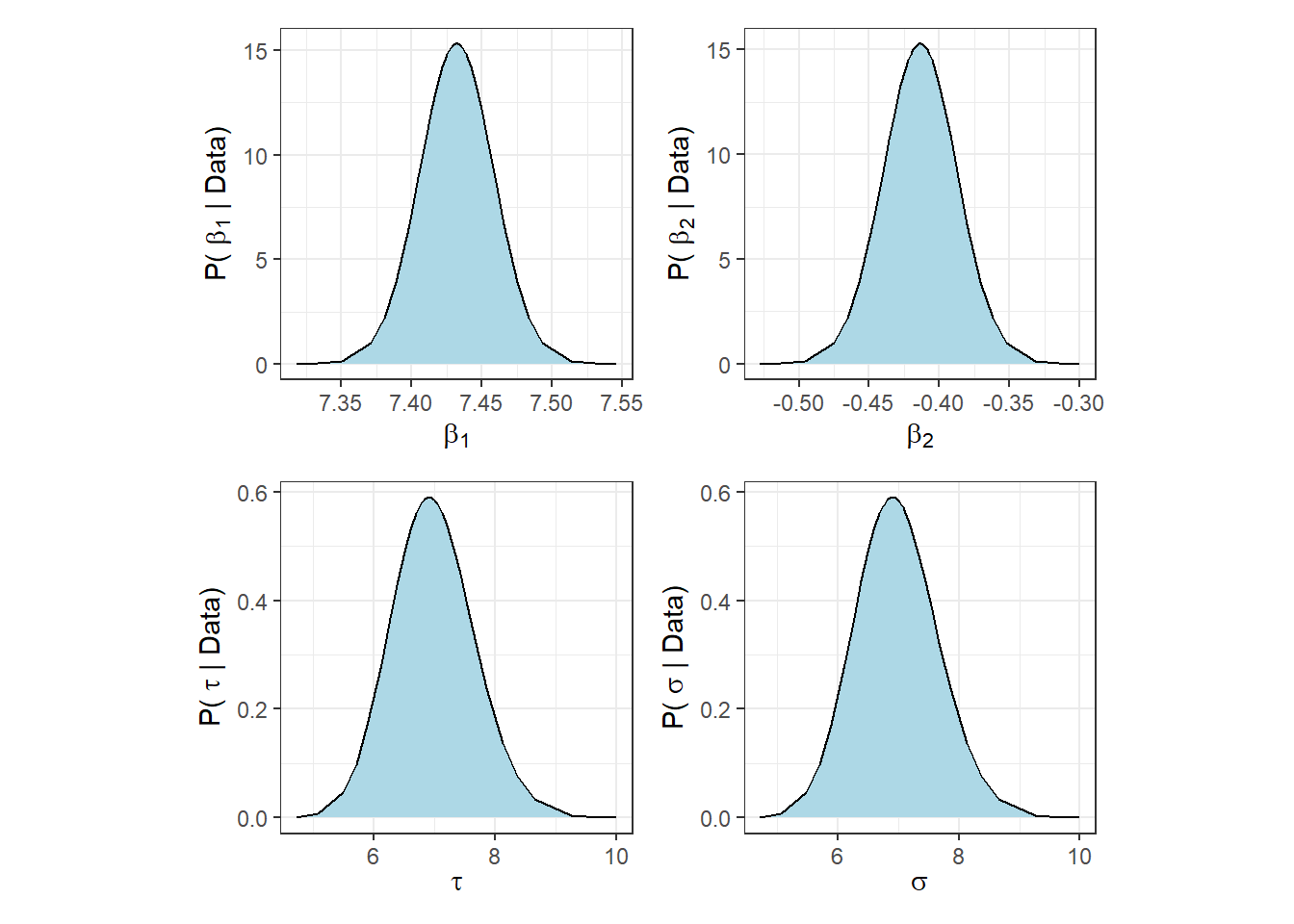

6.9 追記

INLAの詳しい使い方やそれを用いたモデリングについての詳しい解説は、以下の本が役に立つ。いずれも無料でオンラインで閲覧可能である。

• Bayesian inference with INLA
  
• Bayesian Regression Modeling with INLA⁶
  
• Advanced Spatial Modeling with Stochastic Partial Differential Equations Using R and INLA
  
• Dynamic Time Series Models using R-INLA: An Applied Perspective

References

Kruschke J (2014) Doing bayesian data analysis: A tutorial with r, JAGS, and stan. Academic Press

McElreath R (2020) Statistical rethinking : A bayesian course with examples in R and STAN, 2nd Edition. Chapman; Hall/CRC

Ntzoufras I (2011) Bayesian modeling using WinBUGS. John Wiley & Sons

Steidl RJ, Griffin CR, Niles LJ (1991) Contaminant levels of osprey eggs and prey reflect regional differences in reproductive success. J Wildl Manage 55:601–608

Zuur AF (2017) Beginner’s guide to spatial, temporal and Spatial-Temporal ecological data analysis with R-Inla: Using glm and glmm volume I. Hightland Statistics Ltd.

岡田謙介, 大久保街亜 (2012) 伝えるための心理統計: 効果量・信頼区間・検定力. https://core.ac.uk/download/pdf/71788227.pdf; 勁草書房

松浦健太郎 (2016) Stan と R でベイズ統計モデリング (wonderful R 2). 共立出版

馬場真哉 (2019) R と stan ではじめるベイズ統計モデリングによるデータ分析入門. 講談社

---

1. 正規分布は平均が\(\mu\)、標準偏差が\(\sigma\)のとき、\(p(y) = \frac{1}{\sqrt{2 \pi \sigma^2}} exp\Bigl(-\frac{(y - \mu)^2}{2\sigma^2}\Bigl)\)と書ける。↩︎

2. Zuur (2017) ではJAGSが用いられているが、筆者が使い慣れているうえ、本文中のようなアドバンテージもあるのでStanを用いる。↩︎

3. \(P(A|B) = P(A, B)/P(B)\)である。同様に3つ以上の確率変数についても\(P(A. B|C) = P(A,B,C)/P(C)\)と書ける。また、\(P(A , B , C) = P(A| B , C) \times P(B , C)\)と書ける。最後に、\(P(B|C) = P(B , C)/P(C)\)と書ける。これらを全て合わせると、\(P(A , B|C) = P(A|B,C) \times P(B|C)\)と書ける。↩︎

4. MCMCで求めていた事後分布も同様に事後周辺分布である。↩︎

5. 事後分布から分布密度がある値以上をとる区間を切り出した場合に、当該%となる様な区間。↩︎

6. この本では、INLAをサポートするパッケージとしてbrinlaパッケージが開発されている。関数の説明はこちら。分析例はこちら↩︎