14 Spatial-temporal models for orange crowned warblers count data

14.1 Introduction

本章では、競争の強さと捕食圧がサメズアカアメリカムシクイのコドモの数に及ぼす影響を調べた Sofaer et al. (2014) のデータを用いる。それぞれの巣の産卵数が個体密度と年間降水量の関数としてモデル化されている。データは2003年から2009年の7年間取得されている。

ocw <- read_delim("data/OrangedCrownedWarblers.txt")

ocwcoords <- st_as_sf(ocw,
                      coords = c("Xloc", "Yloc"),
                      crs = "+proj=utm +zone=11")

## 緯度経度に変換
lonlat <- st_transform(ocwcoords, crs = "+proj=longlat")

## 元のデータフレームに緯度と経度を追加  
ocw %>% 
  mutate(lon = st_coordinates(lonlat)[,1],
         lat = st_coordinates(lonlat)[,2]) -> ocw


datatable(ocw,
          options = list(scrollX = 30),
          filter = "top")


各巣の位置を年ごとに示したのが以下の図である。年ごとにサンプリング場所とその数は異なっている。

ocw %>% 
  ggplot(aes(x =lon, y = lat))+
  geom_point()+
  theme_bw()+
  coord_fixed(ratio = 1)+
  facet_rep_wrap(~Year, repeat.tick.labels = TRUE)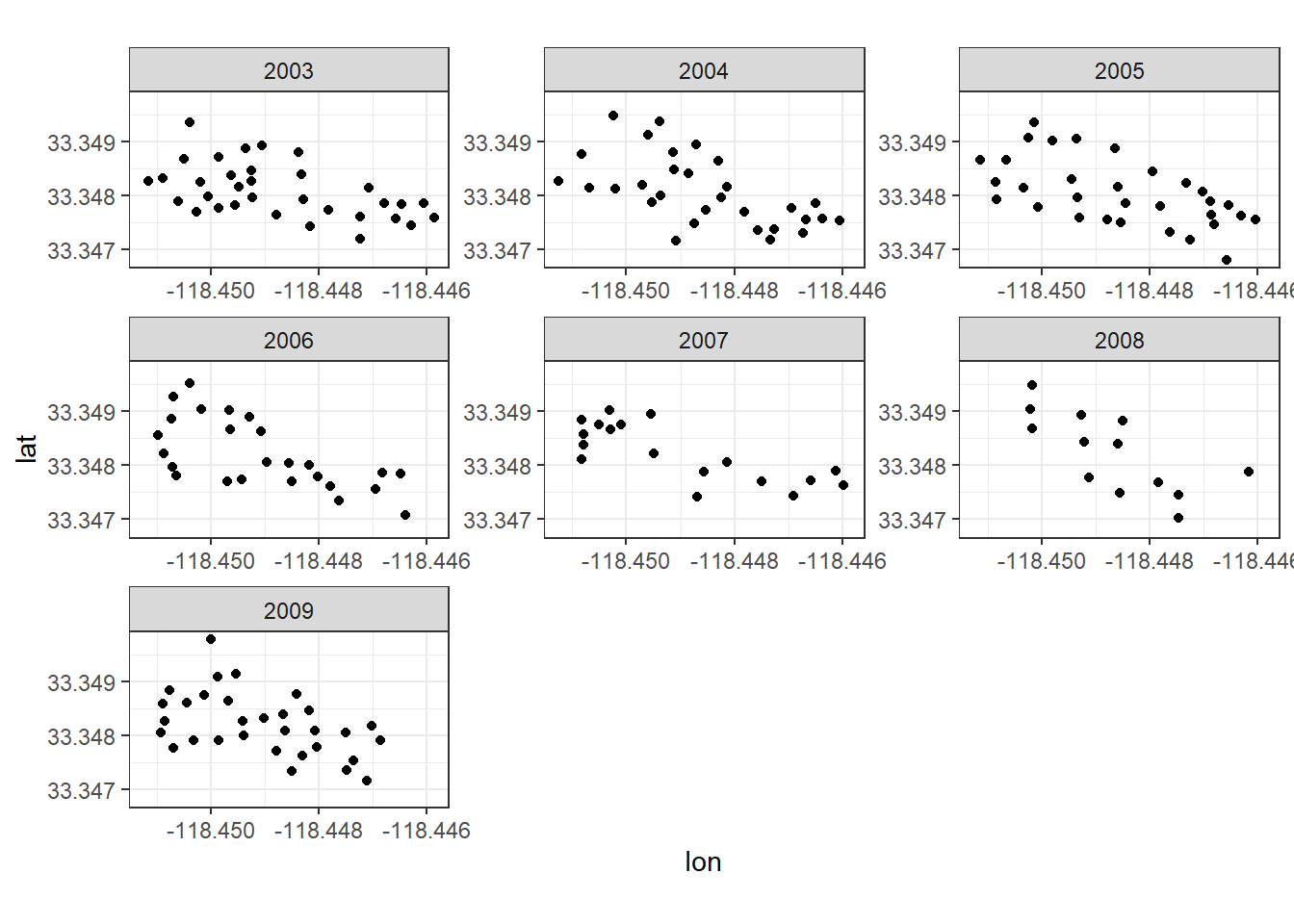

14.2 Poisson GLM

まずは、時空間相関を考えずに通常のポワソンGLMを適用する。FLは雛の数、BreedingDは繁殖ペアの密度、Rainは年間降水量である。

\[ \begin{aligned} &FL_i \sim Poisson(\mu_i)\\ &log(\mu_i) = \beta_1 + \beta_2 \times BreedingD_i + \beta_3 \times Rain_i \end{aligned} \]

モデル化にあたり、変数を標準化する。

ocw %>% 
  mutate(BD_std = (BreedingDensity - mean(BreedingDensity))/sd(BreedingDensity),
         Rain_std = (Precip - mean(Precip))/sd(Precip)) -> ocw

モデルは以下のように実行する。

m15_1 <- inla(NumFledged ~ 1 + BD_std + Rain_std,
              family = "poisson",
              data = ocw,
              control.compute = list(dic = TRUE,
                                     config = TRUE))

それでは、このモデルの診断を行う。ピアソン残差は以下のように計算できる。

fit15_1 <- m15_1$summary.fitted.values$mean
E15_1 <- (ocw$NumFledged - fit15_1)/sqrt(fit15_1)

14.2.1 Overdispersion -approach 1

まずは、過分散を確かめるために分散パラメータを計算する。結果は1.595…であり、やや過分散が生じていることが分かる。

sum(E15_1^2)/(nrow(ocw) - nrow(m15_1$summary.fixed))
## [1] 1.595332

14.2.2 Overdispersion -approach 2

第9.1.3.1.2節で見たように、ベイズモデリングではシミュレーションによって過分散を検討する方がより適切である。以下でシミュレートされたデータと実データを比較する。

set.seed(123)

## 事後分布からサンプリング  
nsim <- 1000
sim_param <- inla.posterior.sample(n = nsim,
                                   result = m15_1)

## シミュレーションデータのぴ話損残差の平方和を計算
y_sim <- matrix(nrow = nrow(ocw),
                ncol = nsim)
sum_E2_sim <- vector()

for(i in 1:1000){
 y_sim[,i] <- rpois(n = nrow(ocw), lambda = exp(sim_param[[i]]$latent[1:nrow(ocw),])) 
 E <- (y_sim[,i] - fit15_1)/sqrt(fit15_1)
 sum_E2_sim[i] <- sum(E^2)
}

実データとシミュレーションデータの観測値の頻度を比較したのが図14.1である。明らかに観測値の方が0が多く、また分布の裾が狭いことが分かる。1も極端に少ない。

data.frame(y_sim) %>% 
  pivot_longer(everything()) %>% 
  group_by(name, value) %>% 
  summarise(N = n()) %>% 
  ungroup() %>% 
  mutate(Freq = N/181) %>% 
  group_by(value) %>% 
  summarise(Frequency = mean(Freq)) %>% 
  ungroup() %>% 
  rename(NumFledged = 1) %>% 
  mutate(type = "Simulated") -> freq_sim

ocw %>% 
  group_by(NumFledged) %>% 
  summarise(N = n()) %>% 
  mutate(Frequency = N/181) %>% 
  ungroup() %>% 
  select(-2) %>% 
  mutate(type = "Observed") %>% 
  bind_rows(freq_sim) %>% 
  complete(NumFledged,  type) %>% 
  ggplot(aes(x = NumFledged, y = Frequency))+
  geom_col(aes(fill = type),
           position = position_dodge(0.95))+
  scale_fill_nejm()+
  scale_x_continuous(breaks = seq(0,15,1))+
  theme_bw()+
  theme(legend.position = c(0.9,0.9),
        aspect.ratio = 0.8)+
  labs(fill = "", x = "Number of fledged chixks")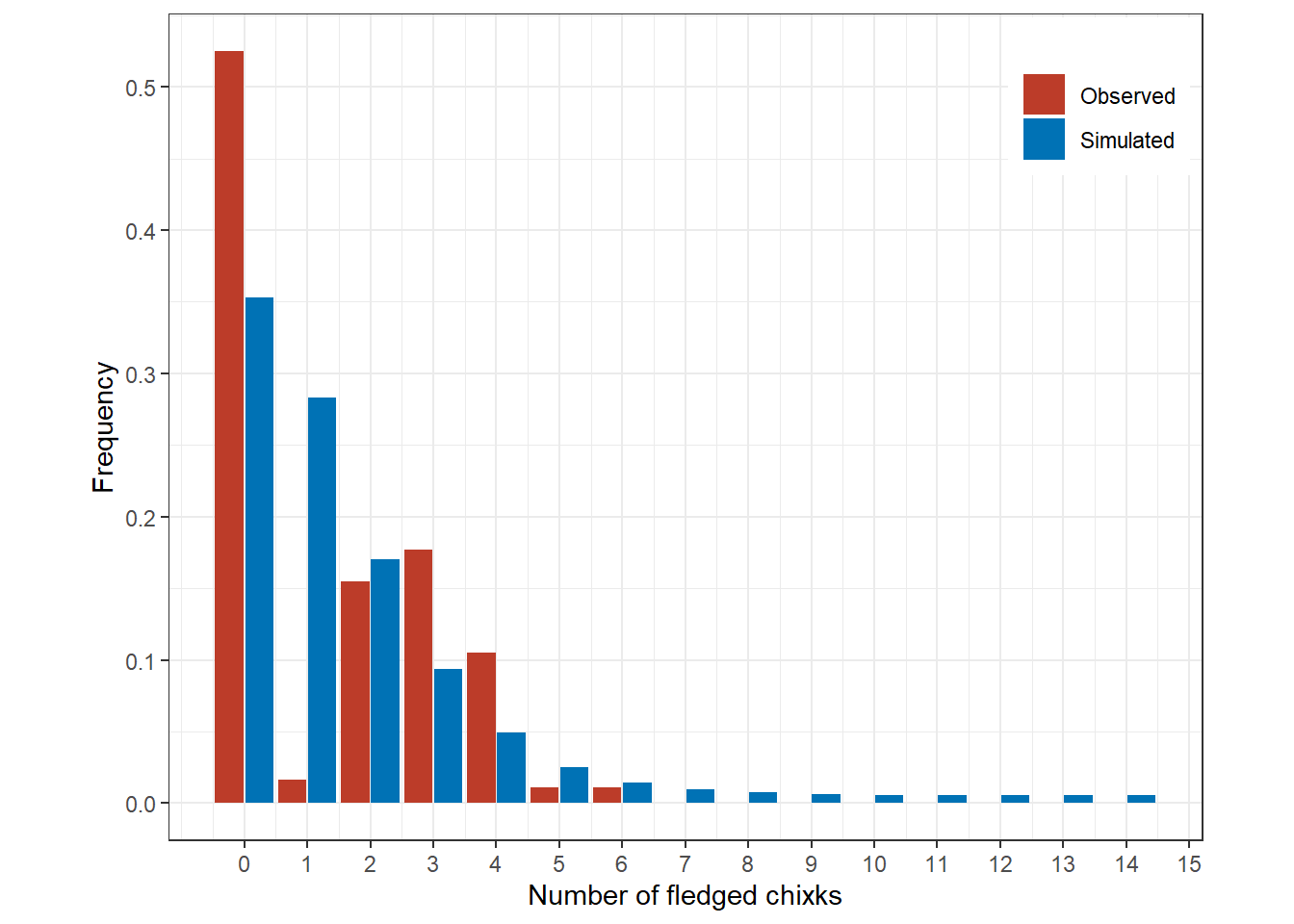
Simulated frequencies (blue) and observed frequencies (red).

図14.1: Simulated frequencies (blue) and observed frequencies (red).


ピアソン残差の平方和の比較も行う。ヒストグラムがシミュレーションデータのピアソン残差の平方和の分布で、赤い点線が実データのものである。実データでは過分散が生じていることが分かる。

data.frame(pr = sum_E2_sim) %>% 
  ggplot(aes(x = pr))+
  geom_histogram(fill = "white",
                 color = "black")+
  theme_bw()+
  theme(aspect.ratio = 1)+
  geom_vline(xintercept = sum(E15_1^2),
             color = "red3",
             linetype = "dashed")+
  geom_text(aes(x = 250, y = 80),
            label = str_c("P = ", mean(sum(E15_1^2) < sum_E2_sim)))+
  labs(x = "Pearson residuals")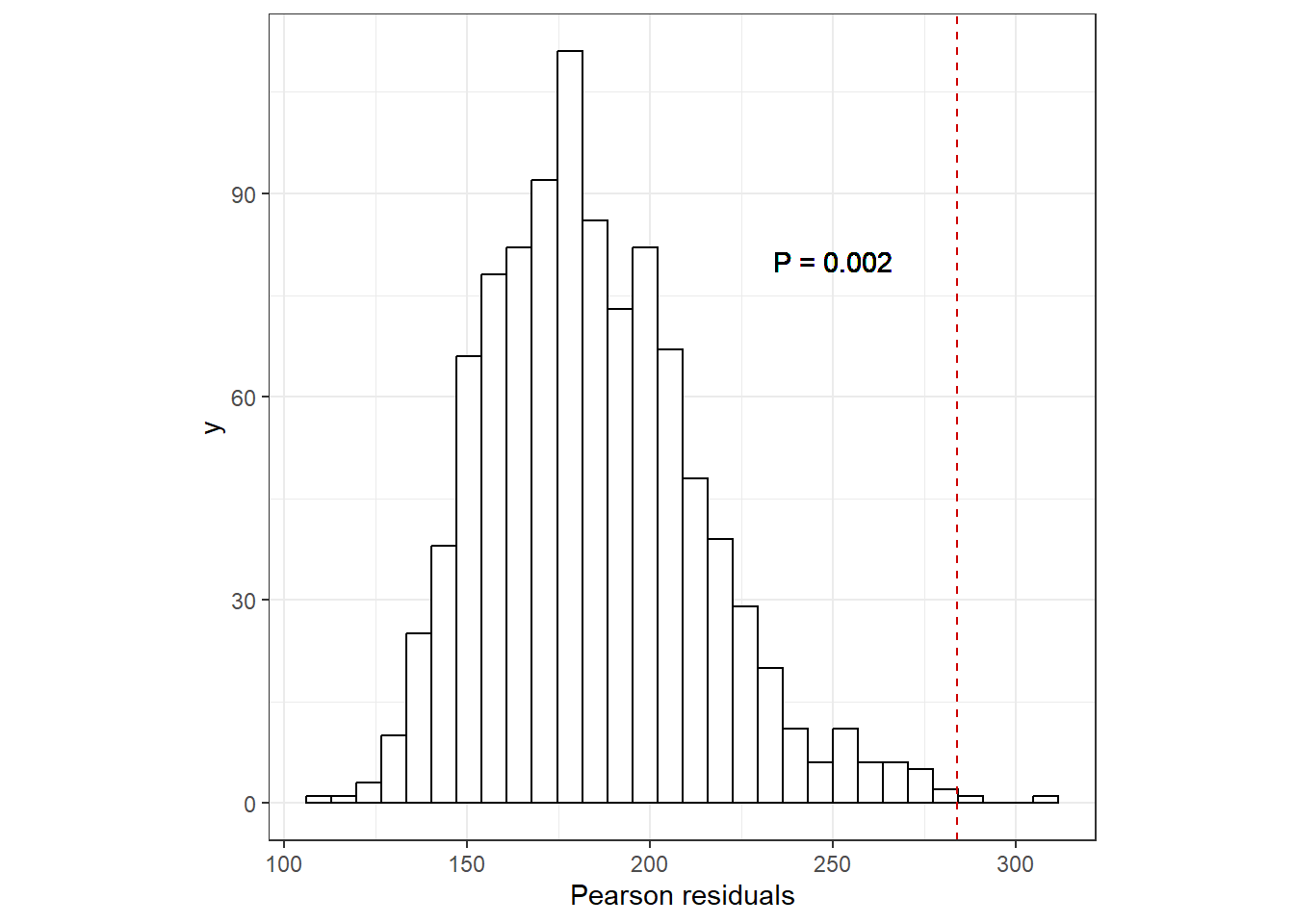

14.3 Model with spatial correlation

続いて、空間相関を考慮したモデルを実行する。モデル式は以下のようになる。共分散行列の成分は、マテルン関数を用いて定義する。

\[ \begin{aligned} &FL_i \sim Poisson(\mu_i)\\ &log(\mu_i) = \beta_1 + \beta_2 \times BreedingD_i + \beta_3 \times Rain_i + u_i\\ &\mathbf{u} \sim GMRF(0, \mathbf{\Omega}) \end{aligned} \]

それでは、第11でデモンストレーションを行った手順通りに準備を行う。まずは、メッシュを作成する。ひとまずは、以下のように作成する。このメッシュには571個の頂点が存在する。

Loc <- cbind(ocw$Xloc, ocw$Yloc)
ConvHull <- inla.nonconvex.hull(Loc)
mesh15_2 <- inla.mesh.2d(boundary = ConvHull,
                         max.edge = 30, cutoff = 1)

続いて、投影マトリックス\(\mathbf{A}\)を定義する。

A15_2 <- inla.spde.make.A(mesh15_2, loc = Loc)

続いて、Matern関数を用いてSPDEを定義する。

spde15_2 <- inla.spde2.matern(mesh15_2, alpha = 2)

また、ランダム空間場\(\mathbf{w}\)を定義する。

w.index15_2 <- inla.spde.make.index("w", mesh15_2$n)

続いて、(切片を含む)共変量の入った行列\(\mathbf{X}\)を作成する。

N <- nrow(ocw)

X <- data.frame(Intercept = rep(1, N),
                BD_std = ocw$BD_std,
                Rain_std = ocw$Rain_std)

最後に、全ての情報を対応付ける。

stk15_2 <- inla.stack(tag = "Fit",
                      data = list(y = ocw$NumFledged),
                      A = list(A15_2, 1),
                      effects = list(w.index15_2,
                                     X))

以上で作成・定義した行列を用いてモデル式は以下のように書ける。

\[ \begin{aligned} &\mathbf{FL} \sim Poisson(\mathbf{\mu})\\ &log(\mathbf{\mu}) = \mathbf{X} \times \mathbf{\beta} + \mathbf{u}\\ &\mathbf{u} = \mathbf{A_2} \times \mathbf{w} \end{aligned} \]

それではモデルを実行する。

f15_2 <- y ~ -1 + Intercept + BD_std + Rain_std + f(w, model = spde15_2)

m15_2 <- inla(f15_2,
              family = "poisson",
              data = inla.stack.data(stk15_2),
              control.compute = list(dic = TRUE,
                                     config = TRUE),
              control.predictor = list(A = inla.stack.A(stk15_2)))

空間相関を考慮しないモデルと比較するとDICはかなり低い。

c(m15_1$dic$dic, m15_2$dic$dic)
## [1] 540.9787 526.4070

14.3.1 Model diagnosis

それでは、モデル診断を行う。先ほどと同様にシミュレーションによってでシミュレートされたデータと実データを比較する。

fit15_2 <- m15_2$summary.fitted.values$mean[1:181]

set.seed(123)

## 事後分布からサンプリング  
nsim <- 1000
sim_param <- inla.posterior.sample(n = nsim,
                                   result = m15_2)

## シミュレーションデータのぴ話損残差の平方和を計算
y_sim <- matrix(nrow = nrow(ocw),
                ncol = nsim)
sum_E2_sim <- vector()

for(i in 1:1000){
 y_sim[,i] <- rpois(n = nrow(ocw), lambda = exp(sim_param[[i]]$latent[1:nrow(ocw),])) 
 E <- (y_sim[,i] - fit15_2)/sqrt(fit15_2)
 sum_E2_sim[i] <- sum(E^2)
}

実データとシミュレーションデータの観測値の頻度を比較したのが図14.2である。m15_1と同様に明らかに観測値の方が0が多く、また分布の裾が狭いことが分かる。1も極端に少ない。

data.frame(y_sim) %>% 
  pivot_longer(everything()) %>% 
  group_by(name, value) %>% 
  summarise(N = n()) %>% 
  ungroup() %>% 
  mutate(Freq = N/181) %>% 
  group_by(value) %>% 
  summarise(Frequency = mean(Freq)) %>% 
  ungroup() %>% 
  rename(NumFledged = 1) %>% 
  mutate(type = "Simulated") -> freq_sim

ocw %>% 
  group_by(NumFledged) %>% 
  summarise(N = n()) %>% 
  mutate(Frequency = N/181) %>% 
  ungroup() %>% 
  select(-2) %>% 
  mutate(type = "Observed") %>% 
  bind_rows(freq_sim) %>% 
  complete(NumFledged,  type) %>% 
  ggplot(aes(x = NumFledged, y = Frequency))+
  geom_col(aes(fill = type),
           position = position_dodge(0.95))+
  scale_fill_nejm()+
  scale_x_continuous(breaks = seq(0,15,1))+
  theme_bw()+
  theme(legend.position = c(0.9,0.9),
        aspect.ratio = 0.8)+
  labs(fill = "", x = "Number of fledged chixks")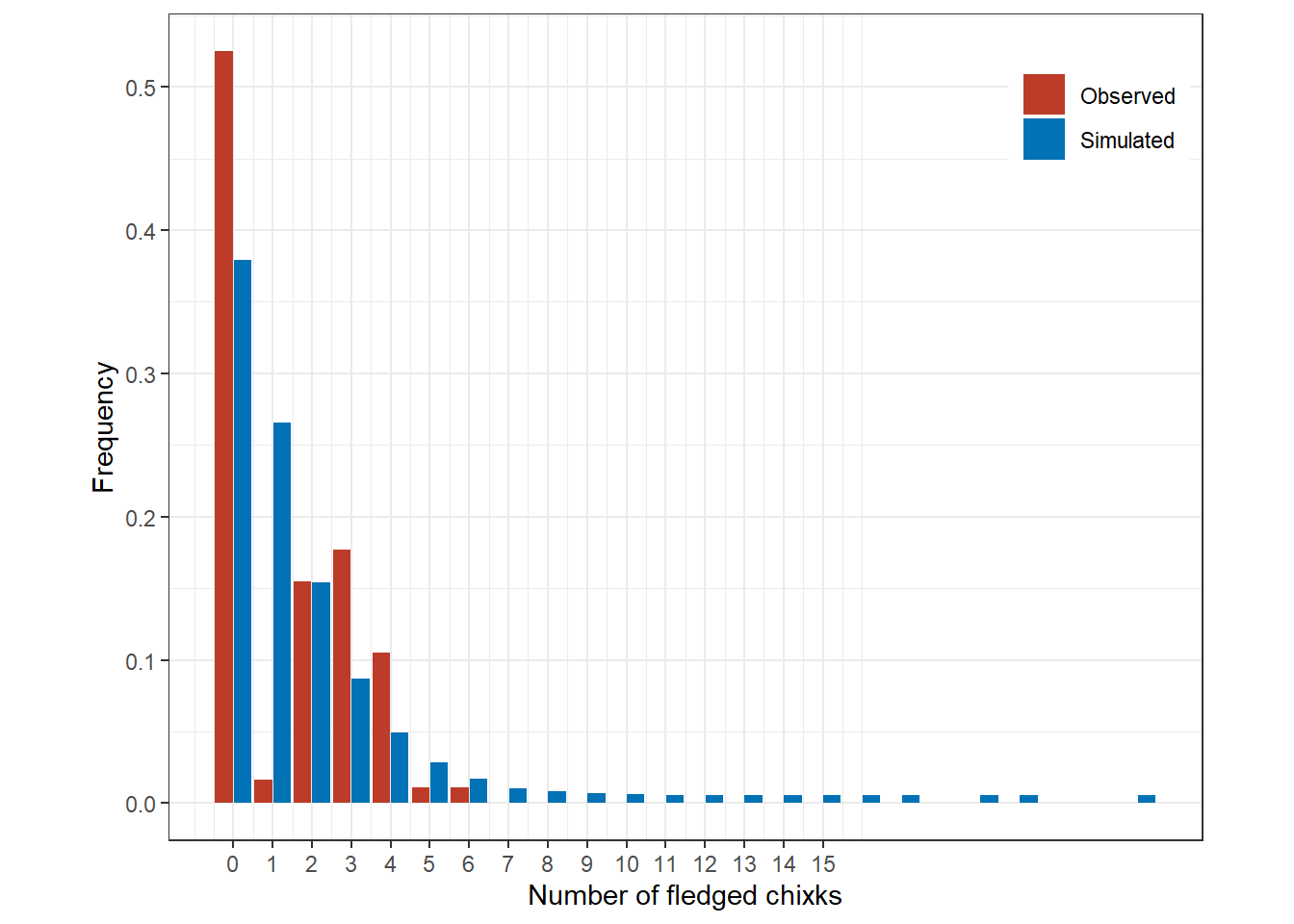
Simulated frequencies (blue) and observed frequencies (red).

図14.2: Simulated frequencies (blue) and observed frequencies (red).


ピアソン残差の平方和の比較も行う。ヒストグラムがシミュレーションデータのピアソン残差の平方和の分布で、赤い点線が実データのものである。過分散は有意水準5%レベルでは生じていないが、やや過分散であることが示唆される。

data.frame(pr = sum_E2_sim) %>% 
  ggplot(aes(x = pr))+
  geom_histogram(fill = "white",
                 color = "black")+
  theme_bw()+
  theme(aspect.ratio = 1)+
  geom_vline(xintercept = sum(E15_1^2),
             color = "red3",
             linetype = "dashed")+
  geom_text(aes(x = 250, y = 80),
            label = str_c("P = ", mean(sum(E15_1^2) < sum_E2_sim)))+
  labs(x = "Pearson residuals")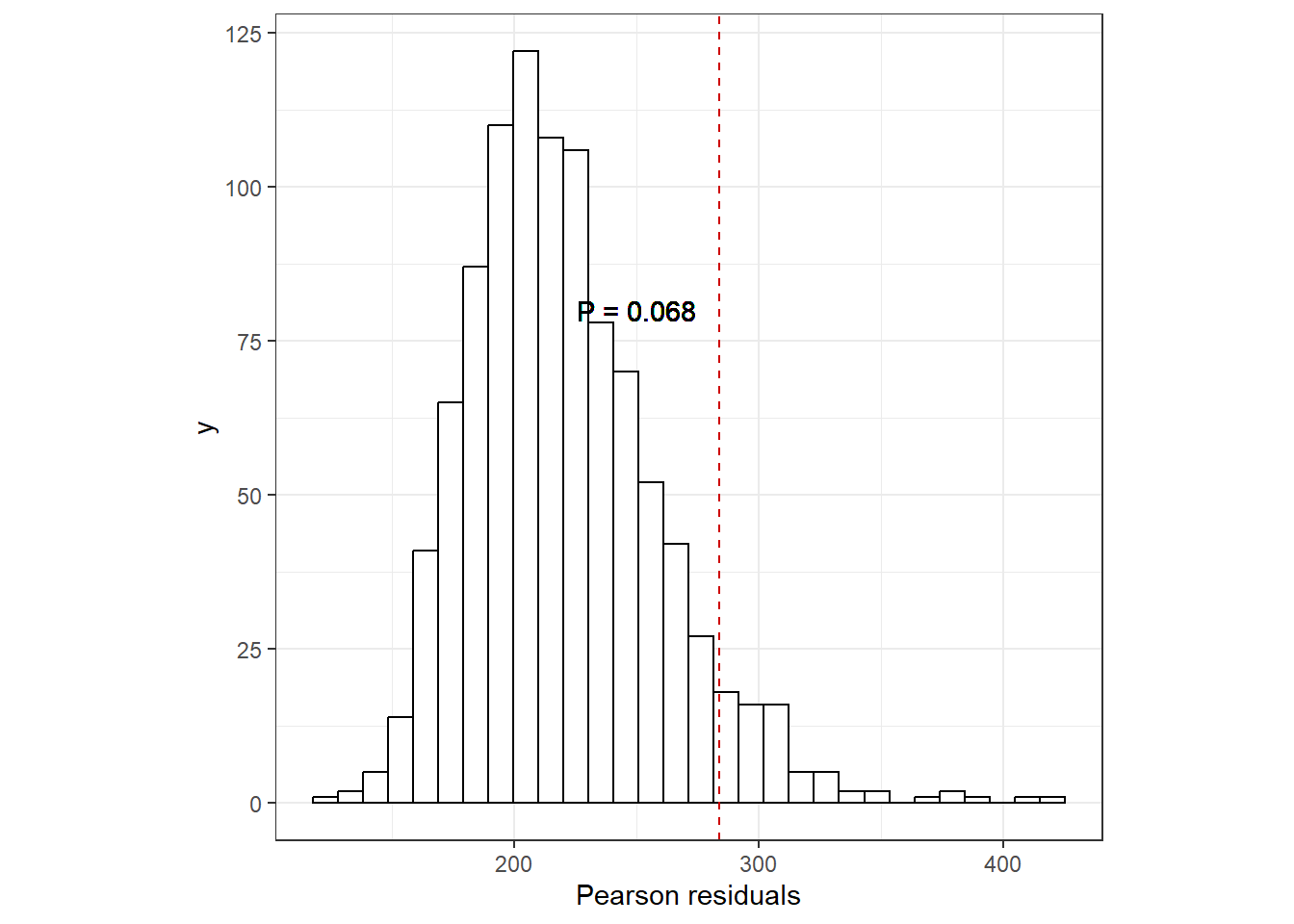


最後に、得られた\(w_k\)と\(u_i\)の事後平均値を座標上に示す。

## wkの算出
w.pm <- m15_2$summary.random$w$mean
w.sd <- m15_2$summary.random$w$sd
wproj <- inla.mesh.projector(mesh15_2)
w.pm100_100 <- inla.mesh.project(wproj, w.pm)
w.sd100_100 <- inla.mesh.project(wproj, w.sd)

expand.grid(X = wproj$x,
        　  Y = wproj$y) %>% 
  mutate(w.pm = as.vector(w.pm100_100),
         w.sd = as.vector(w.sd100_100)) -> w_df

## uの算出
u.proj <- inla.mesh.projector(mesh15_2, loc = Loc)
u.pm <- inla.mesh.project(u.proj,
                          m15_2$summary.random$w$mean)

## 作図
data.frame(X = ocw$Xloc,
           Y = ocw$Yloc,
           u = u.pm) %>% 
  replace_na(list(u = 0)) %>% 
  ggplot(aes(x = X, y = Y))+
  geom_tile(data = w_df %>% drop_na(),
              aes(fill = w.pm))+
  geom_point(aes(shape = u > 0))+
  scale_shape_manual(values = c(1,16))+
  theme_bw() +
  coord_fixed(ratio = 1)+
  coord_cartesian(xlim = c(364900, 365500))+
  scale_fill_gradient2(high = muted("red"), low = muted("yellow4"), mid = "ivory",
                       midpoint = 0)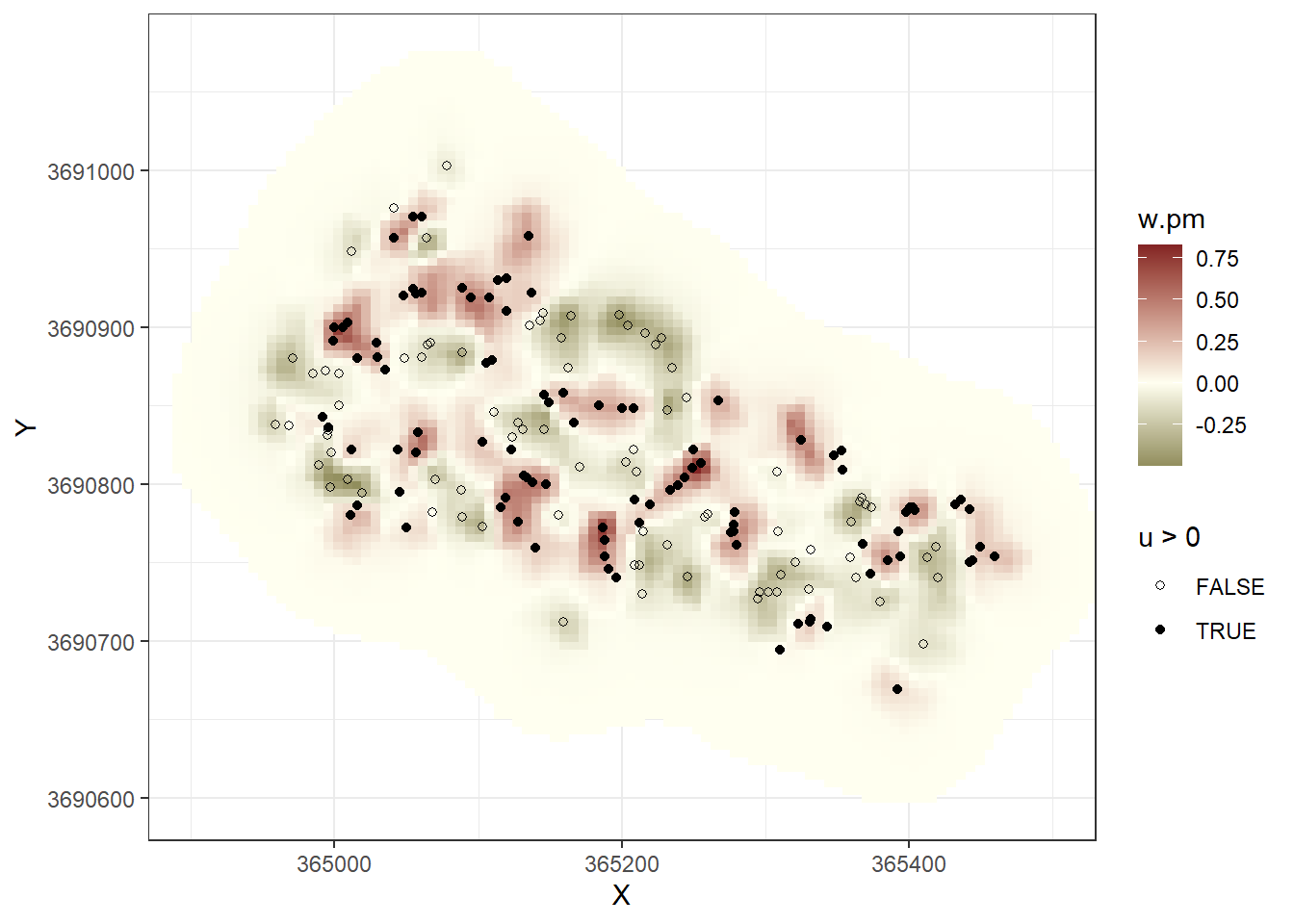

14.4 Spatial-temporal correlation: AR1

それでは最後に、時間的な相関も考慮したモデルを作成する。先ほどのモデルでは、ランダム場は7年間同じであることを仮定していた。しかし、現実では年によってランダム場は変化すると考えた方が自然である。時間的相関を考慮するモデルとして、本節ではAR1モデルを用いる。

14.4.1 Explanation of the model

AR1を用いた時空間モデルは以下のようなモデル式で書ける。なお、\(t\)は年を(\(t = 1,2,3,...,7\))、\(j\)は各年の観察数を表す。\(u_{tj}\)は年ごとに独立して得られるランダム場である。

\[ \begin{aligned} &FL_{tj} \sim Poisson(\mu_{tj})\\ &log(\mu_{tj}) = \beta_1 + \beta_2 \times BreedingD_{tj} + \beta_3 \times Rain_{tj} + v_{tj}\\ &v_{tj} = \phi \times v_{t-1.j} + u_{tj} \end{aligned} \]

14.4.2 Implementation of AR1 model in R-INLA

それでは、実際にINLAで時空間モデルを実装する。

まず、各観察年に番号\(1,2,3,...7\)を割り当てる変数を作成する。

group3 <- ocw$Year - 2002
ngroups <- length(unique(group3))

続いて、投影行列\(\mathbf{A}\)を作成する。このとき、group =に先ほど作成した観察年ごとの番号を当てはめる。

A15_3 <- inla.spde.make.A(mesh15_2,
                          group = group3,
                          loc = Loc)

続いて、ランダム場\(\mathbf{w}\)を定義する。このとき、n.group =で観察年の数を指定する。

w.index15_3 <- inla.spde.make.index(name = "w",
                                    n.spde = mesh15_2$n,
                                    n.group = ngroups)

続いて、これらの情報を紐づける。

stk15_3 <- inla.stack(tag = "Fit",
                      data = list(y = ocw$NumFledged),
                      A = list(A15_3, 1),
                      effects = list(w.index15_3,
                                     X))

それでは、モデルを実行する。モデル式ではgroup = w.group、control.group = list(model = "ar1")とすることで時間的な相関を考慮した空間モデルを実行できる。

f15_3 <- y ~ -1 + Intercept + BD_std + Rain_std + f(w,
                                                    model = spde15_2,
                                                    group = w.group,
                                                    control.group = list(model = "ar1"))

m15_3 <- inla(f15_3,
              family = "poisson",
              data = inla.stack.data(stk15_3),
              control.compute = list(dic = TRUE,
                                     config = TRUE),
              control.predictor = list(A = inla.stack.A(stk15_3)))

DICを比べると、空間相関のみを考慮したモデルよりも少し良い。

c(m15_2$dic$dic, m15_3$dic$dic)
## [1] 526.4070 522.5385

14.4.2.1 Model diagnosis

それでは、モデル診断を行う。先ほどと同様にシミュレーションによってでシミュレートされたデータと実データを比較する。

fit15_3 <- m15_3$summary.fitted.values$mean[1:181]

set.seed(123)

## 事後分布からサンプリング  
nsim <- 1000
sim_param <- inla.posterior.sample(n = nsim,
                                   result = m15_3)

## シミュレーションデータのぴ話損残差の平方和を計算
y_sim <- matrix(nrow = nrow(ocw),
                ncol = nsim)
sum_E2_sim <- vector()

for(i in 1:1000){
 y_sim[,i] <- rpois(n = nrow(ocw), lambda = exp(sim_param[[i]]$latent[1:nrow(ocw),])) 
 E <- (y_sim[,i] - fit15_3)/sqrt(fit15_3)
 sum_E2_sim[i] <- sum(E^2)
}

実データとシミュレーションデータの観測値の頻度を比較したのが図14.3である。m15_1、m15_2と同様に明らかに観測値の方が0が多く、また分布の裾が狭いことが分かる。1も極端に少ない。

data.frame(y_sim) %>% 
  pivot_longer(everything()) %>% 
  group_by(name, value) %>% 
  summarise(N = n()) %>% 
  ungroup() %>% 
  mutate(Freq = N/181) %>% 
  group_by(value) %>% 
  summarise(Frequency = mean(Freq)) %>% 
  ungroup() %>% 
  rename(NumFledged = 1) %>% 
  mutate(type = "Simulated") -> freq_sim

ocw %>% 
  group_by(NumFledged) %>% 
  summarise(N = n()) %>% 
  mutate(Frequency = N/181) %>% 
  ungroup() %>% 
  select(-2) %>% 
  mutate(type = "Observed") %>% 
  bind_rows(freq_sim) %>% 
  complete(NumFledged,  type) %>% 
  ggplot(aes(x = NumFledged, y = Frequency))+
  geom_col(aes(fill = type),
           position = position_dodge(0.95))+
  scale_fill_nejm()+
  scale_x_continuous(breaks = seq(0,30,1))+
  theme_bw()+
  theme(legend.position = c(0.9,0.9),
        aspect.ratio = 0.8)+
  labs(fill = "", x = "Number of fledged chixks")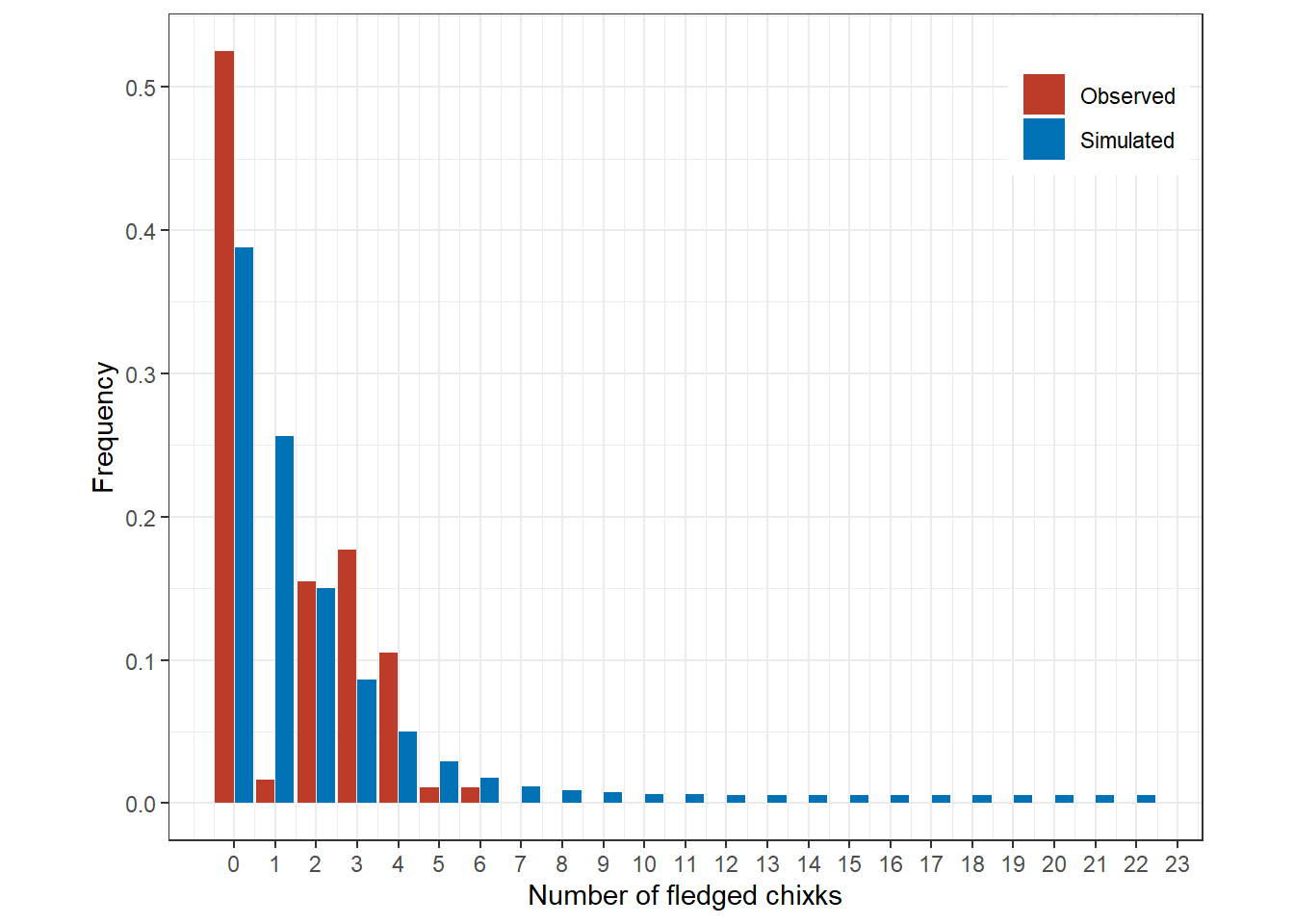
Simulated frequencies (blue) and observed frequencies (red).

図14.3: Simulated frequencies (blue) and observed frequencies (red).


ピアソン残差の平方和の比較も行う。ヒストグラムがシミュレーションデータのピアソン残差の平方和の分布で、赤い点線が実データのものである。過分散は有意水準5%レベルでは生じていない。m15_2よりも過分散は改善している。

data.frame(pr = sum_E2_sim) %>% 
  ggplot(aes(x = pr))+
  geom_histogram(fill = "white",
                 color = "black")+
  theme_bw()+
  theme(aspect.ratio = 1)+
  geom_vline(xintercept = sum(E15_1^2),
             color = "red3",
             linetype = "dashed")+
  geom_text(aes(x = 250, y = 80),
            label = str_c("P = ", mean(sum(E15_1^2) < sum_E2_sim)))+
  labs(x = "Pearson residuals")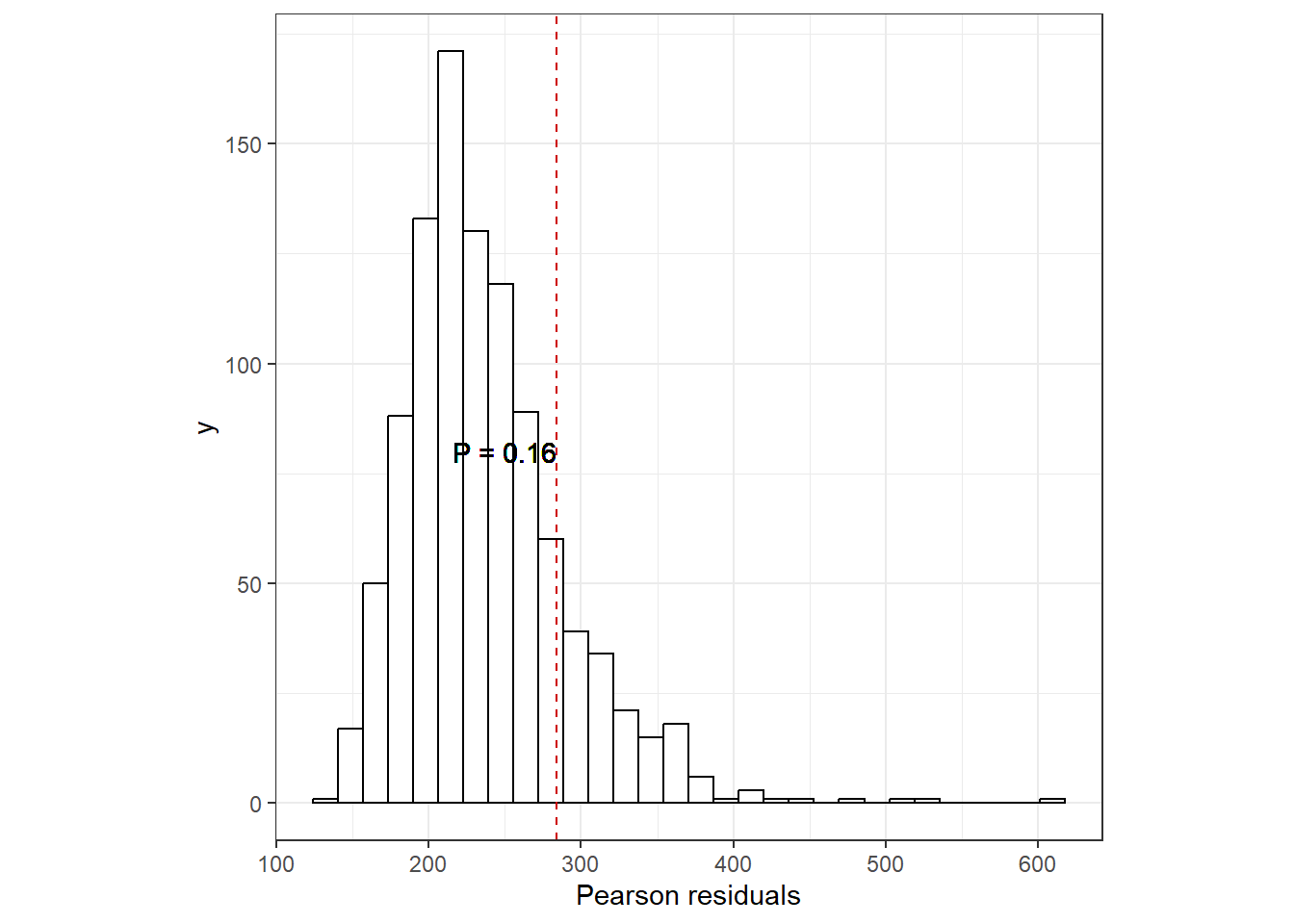


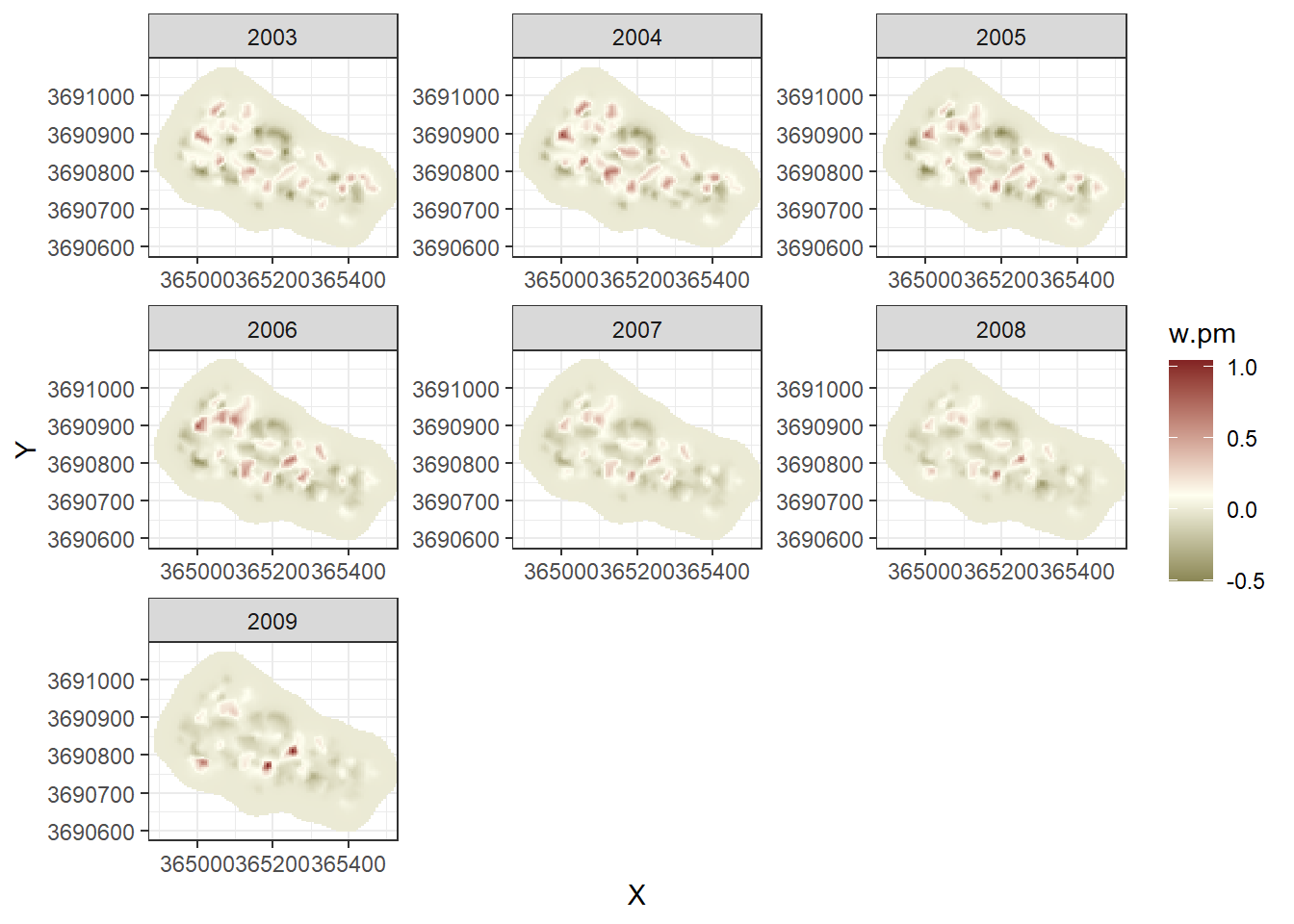
最後に、得られた\(w_k\)の事後平均値を座標上に示す。

## wkの算出
w.pm <- m15_3$summary.random$w$mean
w.sd <- m15_3$summary.random$w$sd
wproj <- inla.mesh.projector(mesh15_2)

w7 <- list()
for (i in 1:7){
   w7[[i]] <- inla.mesh.project(
                      wproj, 
                      w.pm[w.index15_3$w.group==i])
}

expand.grid(X = wproj$x,
        　  Y = wproj$y,
        　  year = 2003:2009) %>% 
  mutate(w.pm = c(as.vector(w7[[1]]), as.vector(w7[[2]]),
                  as.vector(w7[[3]]), as.vector(w7[[4]]),
                  as.vector(w7[[5]]), as.vector(w7[[6]]), as.vector(w7[[7]]))) -> w_df

## 作図
w_df %>% 
  ggplot(aes(x = X, y = Y))+
  geom_tile(data = w_df %>% drop_na(),
              aes(fill = w.pm))+
  scale_shape_manual(values = c(1,16))+
  theme_bw() +
  coord_fixed(ratio = 1)+
  facet_rep_wrap(~year, repeat.tick.labels = TRUE)+
  coord_cartesian(xlim = c(364900, 365500))+
  scale_fill_gradient2(high = muted("red"), low = muted("yellow4"), mid = "ivory",
                       midpoint = 0.1)

References

Sofaer HR, Sillett TS, Langin KM, et al (2014) Partitioning the sources of demographic variation reveals density-dependent nest predation in an island bird population. Ecol Evol 4:2738–2748