5 Modelling space explicitly

本章では、混合モデルのように残差ではなく応答変数に直接従属構造を仮定して空間的相関に対処する方法を見ていく。ただし、通常の混合モデルのランダム切片が正規分布からそれぞれ独立に得られると仮定する一方で、今回はランダム切片が空間的相関を持つことを仮定してモデリングを行う。こうしたモデルの実装を頻度論的な手法で行うことは難しいため、実際のモデリングは次章でベイズ統計について学んでから行う。

5.1 Model formulation

ここでは、前章と同じくシュバシコウのデータ(Bouriach et al. 2015)を用いて話を進める。

まず通常の線形回帰モデルから始めよう。巣IDや雛IDの効果について無視したとき、以下のように書ける。\(i\)はデータの番号を表し、全部で1438ある。
\[ \begin{aligned} BL_i &= \alpha + Age_i \times \beta + \epsilon_i \\ \epsilon_i &\sim N(0,\sigma^2) \end{aligned} \]

このモデルは以下のようにも書ける。なお、\(z_i = (1, Age_i)\)である。1列目の1は切片を表している。\(\bf{\beta} = \begin{pmatrix} \alpha\\ \beta \end{pmatrix}\)である。
\[ \begin{aligned} BL_i &= z_i \times \bf{\beta} + \epsilon_i\\ \epsilon_i &\sim N(0,\sigma^2) \end{aligned} \tag{5.1} \]

式(5.1)は単純な線形回帰モデルであり、残差はそれぞれ正規分布から独立に得られると仮定されている。\(\bf{\epsilon} = (\epsilon_1, \epsilon_2, \dots, \epsilon_{1438})\)とするとき、\(\bf{\epsilon} \sim N(0,\bf{\Sigma})\)と書ける。なお、\(\bf{\Sigma}\)は\(\bf{I}\)を単位行列とするとき\(\sigma^2 \times \bf{I}\)と書ける。第2で見たように、このとき\(\bf{\Sigma}\)は対角成分以外が0の行列なので、残差同士の相関は0であると仮定されている。

そこで、空間的な相関に対処するために式(5.1)に空間的相関を表す要素を付け足す。本書では、これを\(u_i\)と表す。

\[ \begin{aligned} BL_i &= z_i \times \bf{\beta} + u_i + \epsilon_i\\ epsilon_i &\sim N(0,\sigma^2)\\\ \end{aligned} \tag{5.2} \]

ここで、\(u_i\)は平均が0で、分散共分散行列が\(\bf{\Omega}\)に従う正規分布から得られると考える。ただし、\(\bf{\Omega}\)は通常のランダム切片のように対角行列(対角成分以外が0の行列)ではなく、空間相関を考慮している。

よって、このモデルは以下のように書ける。

\[ \begin{aligned} BL_i &= z_i \times \bf{\beta} + u_i + \epsilon_i\\ \bf{\epsilon} &\sim N(0,\sigma^2 \times \bf{I})\\ \bf{u} &\sim N(0, \bf{\Omega}) \end{aligned} \tag{5.3} \]

5.2 Covariance matrix of the spatial random effect

\(\bf{\Omega}\)の成分全てを推定するのは非常に難しい。今回のように1438個のデータがあるのであれば、\(1438 \times 1437 \times 1/2 = 1033203\)このパラメータを推定してければいけなくなる。そこで、第2章(AR1過程)や第3章(バリオグラムモデル)でやったように、推定するパラメータを減らすために何らかの数理モデルを用いる。

ここでは、第3.3節で導入したMatern相関関数を用いる。この関数では、2つのパラメータさえ推定すればよい。

5.2.1 Simulation study

以下では、Matern関数がどのように\(\bf{\Omega}\)を決定するかをシミュレーションを用いて説明する。

以下のように、5つの場所をランダムに定める(図5.1)。

set.seed(123)
Xloc <- runif(5, 0, 1)
Yloc <- runif(5, 0, 1)
Loc <- cbind(Xloc, Yloc)

Loc %>% 
  data.frame() %>% 
  mutate(n = 1:n()) %>% 
  ggplot(aes(x = Xloc, y = Yloc))+
  geom_text(aes(label = n))+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(x = "X coordinates", y = "Y coordinates")+
  scale_x_continuous(breaks = seq(0.3,1,0.1))+
  scale_y_continuous(breaks = seq(0,1,0.2))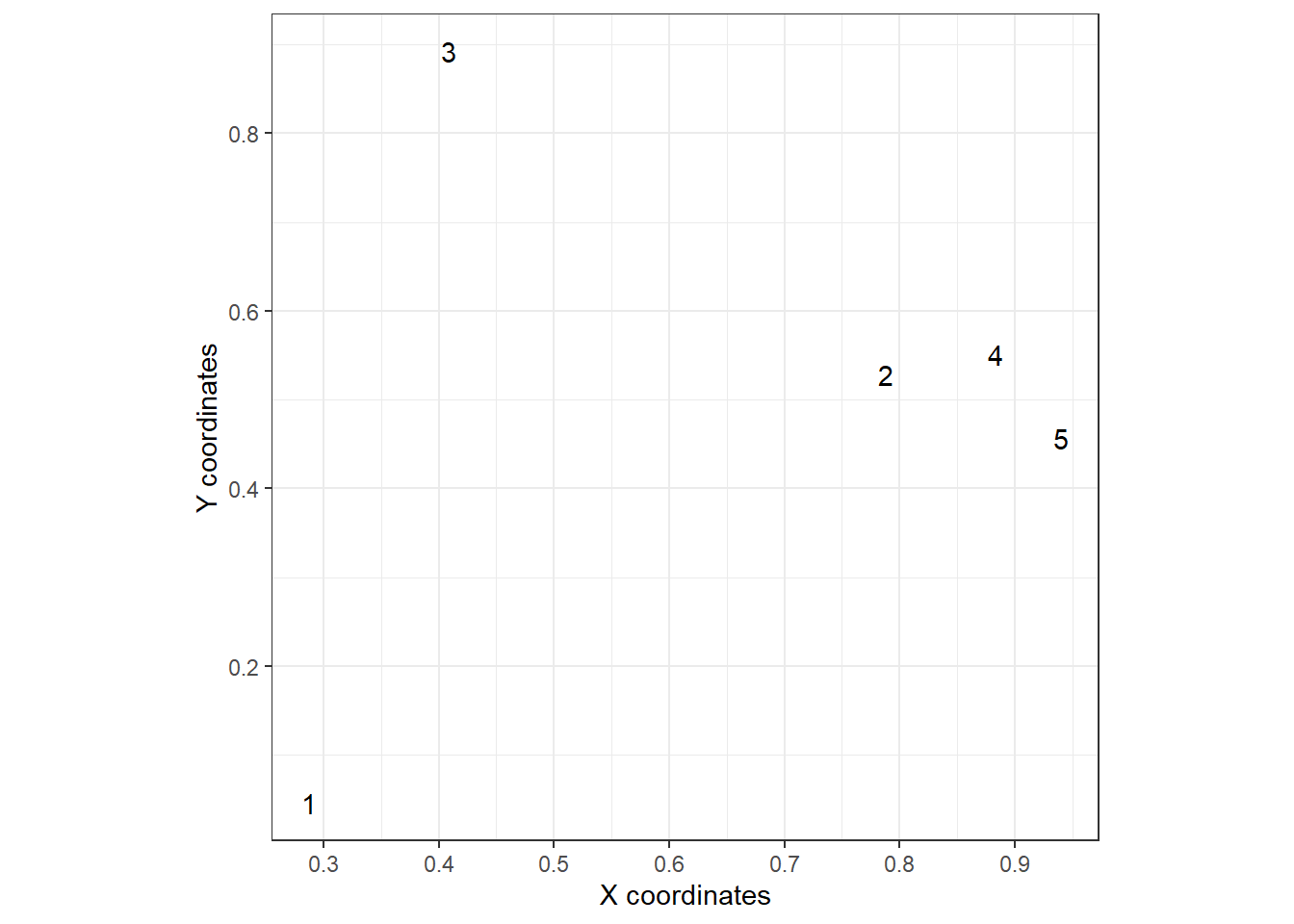
Position of five sampling locations in our simulation study.

図5.1: Position of five sampling locations in our simulation study.


ここで、それぞれの場所で雛のくちばし長のデータを収集したとする。式(5.2)より、5つのランダム切片\(u_1, u_2, \dots, u_5\)を推定する必要がある。\(u_i\)は平均が0、分散共分散行列が\(\bf{\Omega}\)の正規分布から得られるとする。\(\bf{\Omega}\)は以下で与えられるとする。

\[ \bf{\Omega} = \sigma_u^2 \times \begin{pmatrix} 1 & \omega_{12} & \omega_{13} & \omega_{14} & \omega_{15} \\ & 1 & \omega_{23} & \omega_{24} & \omega_{25} \\ & & 1 & \omega_{34} & \omega_{35} \\ & & & 1 & \omega_{45} \\ & & & & 1 \end{pmatrix} \]

ここで、行列の各要素はMatern関数によって定まるとする。第3.3節で見たように、Matern関数は距離と2つの未知のパラメータで定まる関数である。よって、この2つのパラメータが定まれば全ての\(\omega\)が定まる。

\[ \omega_{ij} = cov(u_i,u_j) = \sigma_u^2 \times \rm{Matern \; correlation \; sites \; i \; and\;j} \tag{5.4} \]

それでは、以下で実際にパラメータを定めて\(\omega_{ij}\)を計算してみよう。まず、データ間の距離を算出する。

Dist <- dist(Loc) %>% 
  as.matrix()

Dist
##           1          2         3          4         5
## 1 0.0000000 0.69540037 0.8555197 0.78132050 0.7715140
## 2 0.6954004 0.00000000 0.5259413 0.09754322 0.1681197
## 3 0.8555197 0.52594131 0.0000000 0.58393877 0.6873190
## 4 0.7813205 0.09754322 0.5839388 0.00000000 0.1108665
## 5 0.7715140 0.16811974 0.6873190 0.11086647 0.0000000

次にMatern関数のパラメータを定める。ここでは、\(\kappa = 4, \nu = 1\)とする。また、\(\sigma_u\)も1とする。

kappa <- 5
nu <- 1
sigma_u <- 1

式(5.4)より、\(\omega_{ij}\)は以下のように求まる。

d.vec <- as.vector(Dist)
cor.M <- sigma_u * (2^(1-nu))/gamma(nu) * (kappa * d.vec)^nu * besselK(kappa*d.vec, nu)

\(\omega_{ij}\)と距離の関係を図示すると以下のようになる。ここからわかるように、距離が近いほど共分散\(\omega_{ij}\)が大きくなっている。

data.frame(dist = d.vec,
           omega = cor.M) %>% 
  drop_na() %>% 
  ggplot(aes(x = dist, y = omega))+
  geom_line()+
  theme_bw()+
  theme(aspect.ratio = 1)+
  labs(x = "Distance", y = "Covariance")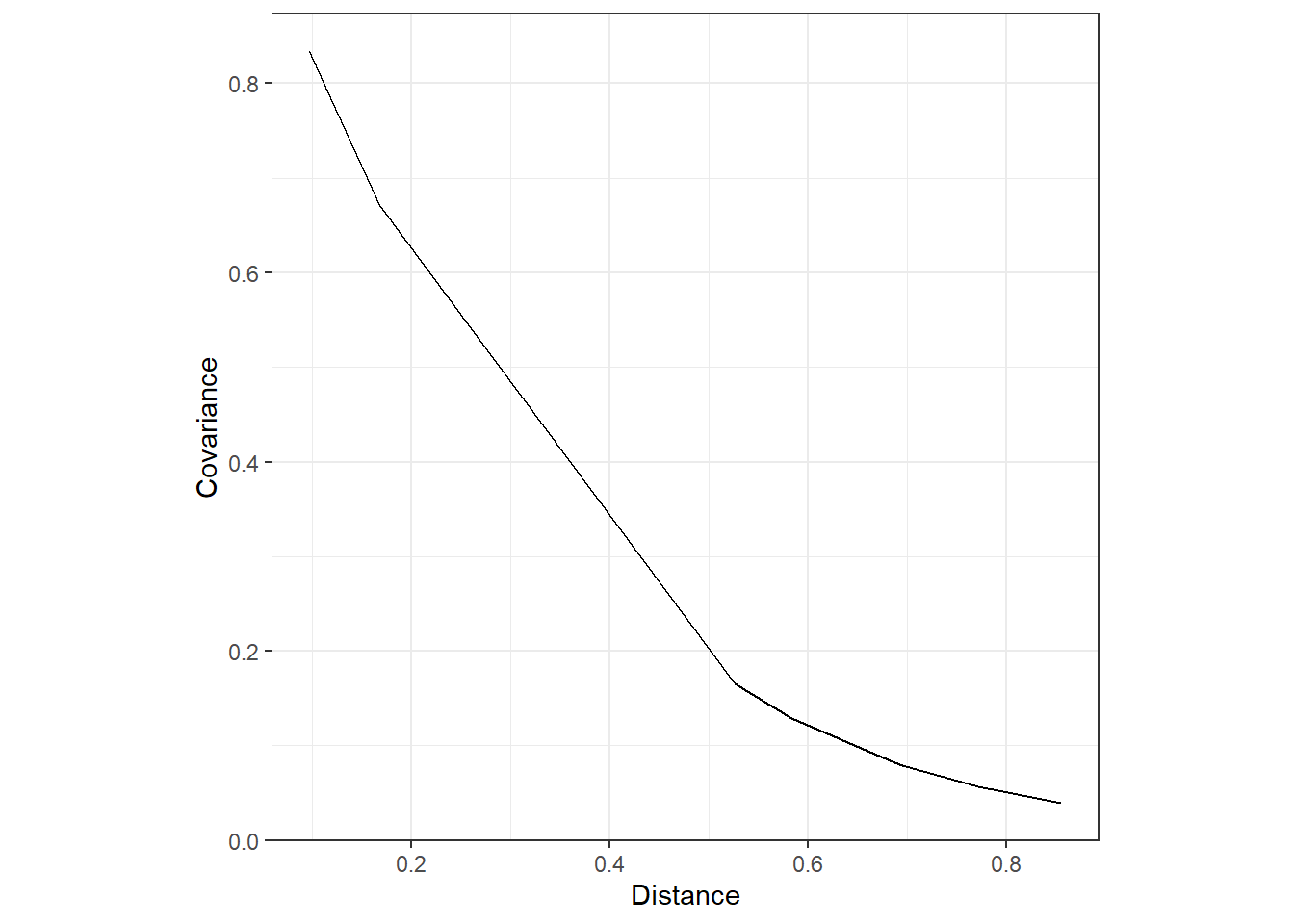

行列\(\bf{\Omega}\)は以下の通り。図5.1と見比べると、実際に距離が近いデータほど値が高くなっていることが分かる(e.g., 2と4、4と5)。

omega <- matrix(cor.M, ncol = 5, nrow = 5)
diag(omega) <- 1
colnames(omega) <- 1:5
rownames(omega) <- 1:5

omega %>% 
  kable(digits = 3, align = "c", caption = "Ω") %>% 
  kable_styling(font_size = 15, full_width = FALSE)
表5.1: Ω
1 2 3 4 5
1.000 0.079 0.039 0.054 0.057
0.079 1.000 0.166 0.834 0.671
0.039 0.166 1.000 0.129 0.082
0.054 0.834 0.129 1.000 0.803
0.057 0.671 0.082 0.803 1.000


以上をまとめると、以下のようになる。

  1. データ間の空間的相関を決める分散共分散行列\(\bf{\Omega}\)をMatern関数を用いて定義する。
  2. Matern関数では、距離が近いほど\(\bf{\Omega}\)の行列成分\(\omega\)の値が大きくなり、ひいては\(u_i\)の値が近くなっていく。

第8章以降では、INLAというパッケージを用いて式(5.2)をモデリングしていく。

5.3 Spatial-temporal correlation

ここまで時系列相関と空間相関について別々に扱ってきたが、現実のデータではどちらもが同時に存在することが多々ある。例えば、シュバシコウのデータ(Bouriach et al. 2015)では様々な巣において4年間にわたるデータが収集された。

以下では、再びシュバシコウのデータを用いて空間モデルを時空間モデル(spatial-temporal model)に拡張していく。\(BL_{it}\)を場所\(i\)、時間\(t\)におけるくちばし長、\(Z_i = (1, Age_{it})\)とするとき、以下のようにモデルを拡張する。

\[ \begin{aligned} BL_i &= z_i \times \bf{\beta} + w_{it} + \epsilon_i\\ epsilon_i &\sim N(0,\sigma^2)\\\ \end{aligned} \tag{5.5} \]

なお、\(w_{it}\)は時系列相関を考慮するため以下のように定式化する。\(\phi\)は-1から1までの値をとるパラメータである。\(w_{it}\)は\(\phi\)が大きいほど1時点前の\(w_{i,t-1}\)と類似する。
\[ w_{it} = \phi \times w_{i, t-1} + u_{it} \]

5.3.1 Simulation study (continued)

\(u_{it}\)は空間相関を表す項で、第5.2と同様に平均0, 分散共分散行列が\(\bf{\Omega}\)の正規分布から得られるとする。

\[ \begin{pmatrix} u_{1t}\\ \vdots\\ u_{5t} \end{pmatrix} \sim N(0, \bf{\Omega}) \]

式(5.4)と同様に、\(\bf{\Omega}\)は以下のように書ける。なお、\(u_{it}\)には時間的な相関はない。

\[ \bf{Omega} = \sigma_u^2 \times \rm{Matern \; correlation \; sites \; i \; and\;j} \]

それでは、\(w_{it}\)がどのように決まるか実際にシミュレーションを行ってみよう。

まず、時間的当館が強く、\(\phi = 0.9\)であるとする。

phi <- 0.9

100時点(\(t = 1,2,3,\dots,100\))のデータが5地点(\(i = 1,2,\dots,5\))について収集されたとする。このとき、時点1のデータ\(w_{i,1}\)は以下のように得られる(数学的な詳細はここでは省略)。

\[ \begin{pmatrix} w_{1,1}\\ \vdots\\ w_{5,1} \end{pmatrix} \sim N(0, \frac{\sigma_u^2}{1-\phi^2} \times \bf{\Omega}) \]

なお、\(\sigma_u^2 = 1\)であるとし、\(\bf{\Omega}\)は前節と同じものを使用する。以下で\(w_{i,1}\)が得られた。

sigma_u <- 1
cov.w1 <- (sigma_u^2/(1-phi^2))+omega
w1 <- mvrnorm(1, mu = rep(0,5), Sigma = cov.w1)

よって、\(t = 2,3,\dots,100\)のときの\(w_{it}\)っは以下のように得られる。

w <- matrix(nrow = 5, ncol = 100)
w[,1] <- w1
colnames(w) <- str_c("t", 1:100)

for(t in 2:100){
  u <- mvrnorm(1, mu = rep(0,5), Sigma = omega)
  w[, t] <- phi*w[t-1] + u
}

以下のように5地点における100時点の\(w_{it}\)が得られた。

w %>% 
  data.frame() %>% 
  rownames_to_column(var = "place") %>% 
  mutate_if(is.numeric, ~round(.,3)) %>% 
  datatable(options = list(scrollX = 20),
            filter = "top")


これを図示すると以下のようになる。場所が近い地点のデータ(2,4,5)はそれ以外のデータよりもより類似している傾向があることが分かる。

w %>% 
  data.frame() %>% 
  rownames_to_column(var = "place") %>% 
  pivot_longer(2:101, names_to = "time", values_to = "w") %>% 
  mutate(time = as.numeric(str_replace(time, "t",""))) %>% 
  ggplot(aes(x = time, y = w))+
  geom_line(aes(linetype = place,
                linewidth = place %in% c("2","4","5")))+
  scale_linewidth_manual(values = c(0.6,1.2))+
  theme_bw()+
  theme(aspect.ratio = 0.8)+
  labs(linewidth = "if place is 2, 4, or 5")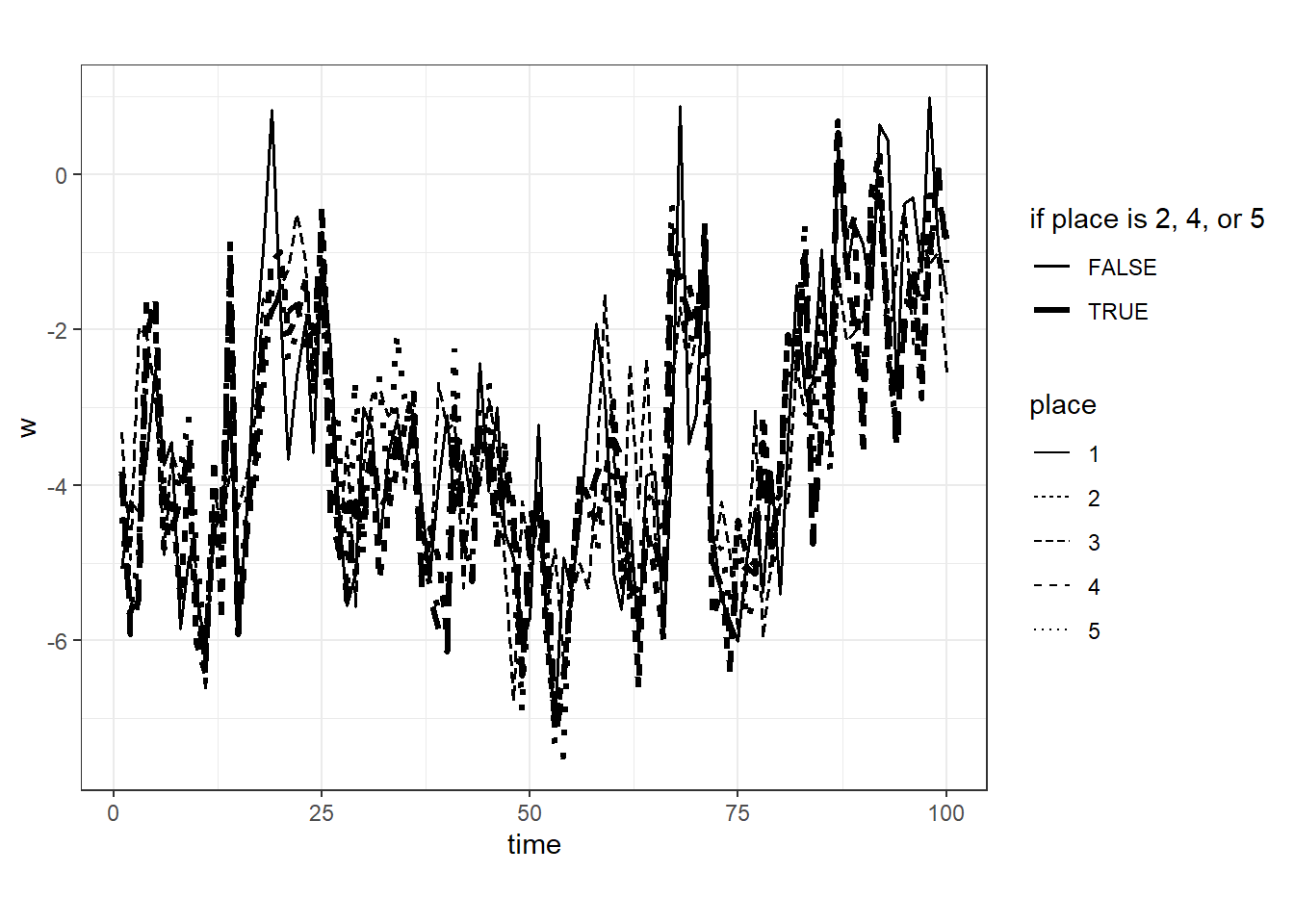


実際の分析では、\(w_{it}\)を得るためのパラメータ(\(\phi, \sigma_u, \kappa, \nu\)は与えられるものではなく、データから推定することになる。データの推定は非常に複雑なので、ベイズ推定が必要になってくる。次章ではベイズ統計について学ぶ。

References

Bouriach M, Samraoui F, Souilah R, et al (2015) Does Core-Periphery gradient determine breeding performance in a breeding colony of white storks ciconia ciconia? AORN J 50:149–156