3.2 ネットワーク構造の諸指標
ここでは、ネットワーク全体の構造の特徴を表す指標についてまとめる。
3.2.1 集中度(Centralization)
前節では、各ノードがグラフ内でどの程度中心的かを表す指標として中心性指標を扱ってきた。それらを用いてグラフにおいて特定のノードに高い中心性がどの程度集中しているのかを示す指標が集中度である。グラフの集中度(\(C_x\))は以下の式によって定式化され、0から1の値をとる。ただし、各ノードの中心性指標を\(C_x(i)\)、グラフにおけるその中心性指標の最大値を\(C_x(i^*)\)とする。また、そのグラフと同数のノード(n個)を持つグラフにおける\(\sum_{i=1}^n [C_x(i^*)-C_x(i)]\)の最大値を\(max\sum_{i=1}^n [C_x(i^*)-C_x(i)]\)とする。
\(C_x = \frac {\sum_{i=1}^n [C_x(i^*)-C_x(i)]}{max\sum_{i=1}^n [C_x(i^*)-C_x(i)]}\)
例として、第2章で算出した毛づくろい頻度ネットワークgroom_mat_b(表2.5)の集中度を求める。igraphパッケージでは、様々な中心性指標についての中心度を求められる。graph_from_adjacency_matrix()でigraphクラスに変換した後に算出する。
## igraphクラスに変換
graph_groom <- graph_from_adjacency_matrix(groom_mat_b,
## 有向グラフなら "directed"
mode= "undirected",
## 重みなしなら NULL
weighted = TRUE)
## 次数中心性
centr_degree(graph_groom,
## 入次数、出次数ならそれぞれ "in"と"out
mode = "all")$centralization -> cent_deg
cent_deg## [1] 0.2904412## 固有ベクトル中心性
centr_eigen(graph_groom,
## 有向グラフならTRUE
directed = FALSE)$centralization -> cent_eig
cent_eig## [1] 0.3104138## [1] 0.04678902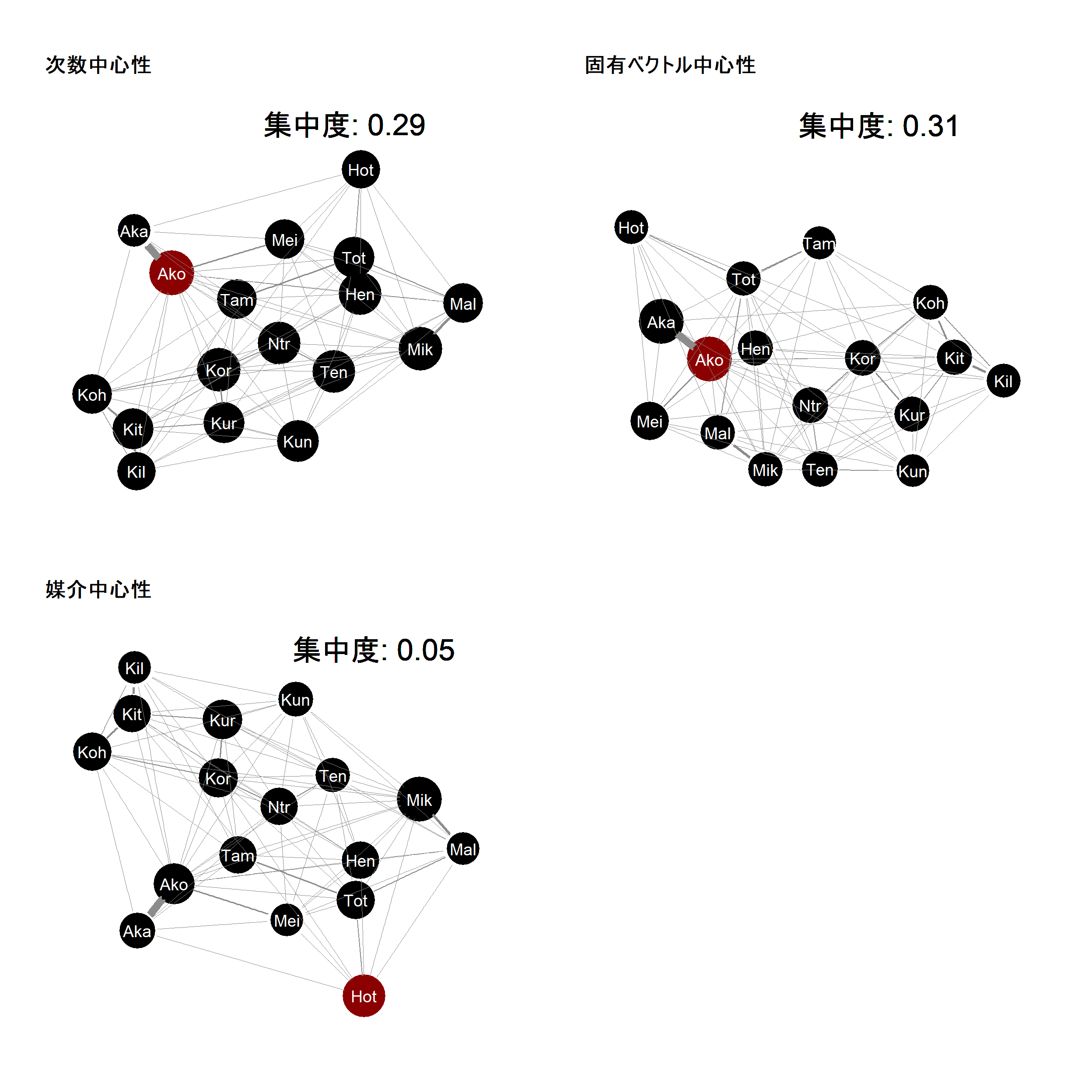
図3.10: 次数中心性・固有ベクトル中心性・媒介中心性の値をノードの大きさに反映したグラフと各指標における集中度。 ノードが赤い個体が各指標の最も大きい個体を示す
3.2.2 密度(Density)
密度は、社会ネットワークにおける関係の緊密さの指標になりうる。密度が低いとき、社会ネットワーク内の個体間の直接的な関係は少なく、両者の関係は媒介者を通じた間接的なものが多いということができる(D. Croft et al., 2008)。
重み無しグラフの場合: 実際の辺の数をグラフに張ることが可能な辺の最大数で割ったもの
ノードの数を\(n\)、実際の辺の数を\(m\)としたとき、\(2m/n(n-1)\)(無向グラフ)または\(m/n(n-1)\)(有向グラフ)重み付きグラフの場合: 全辺の重みの合計をグラフに張ることが可能な辺の最大数で割ったもの
ノードの数を\(n\)、重みの合計を\(w\)としたとき、\(2w/n(n-1)\)(無向グラフ)または\(2m/n(n-1)\)(有向グラフ)
ここでは、表3.1の隣接行列を用いて密度を算出する。
ANTsパッケージでは、met.density()で計算可能。ただし、重みなしグラフとして算出されるよう。また、list()関数で複数の隣接行列をリスト化することで、同時に2つ以上の隣接行列について密度を算出できる。
## Density
## 0.3571429## [[1]]
## [1] 0.3571429
##
## [[2]]
## [1] 0.2678571snaパッケージでは、gden()で計算可能。ignore.value = FALSEとすると重み付きグラフとして扱われる。ANTsパッケージと同様、リスト化した複数の隣接行列の密度を同時に算出できる。
## 重み付き
gden(mat_undir_b,
## 重み無グラフならば、TRUE
ignore.eval = FALSE,
## 有向グラフならば "digraph"
mode = "graph")## [1] 0.6428571## [1] 0.6428571 0.44642863.2.3 同類性(Assortativity)
ネットワーク内において、似ているノード同士が結びつきやすい/結びつきにくいかを表したのが同類性である。ネットワーク内の辺の両端にあるノードの中心性指標や属性の相関係数を算出したものであり、-1から1の値をとる(重み付きグラフの場合は、それで重み付けされているよう)。各ノードの離散的な属性(性別、順位カテゴリなど)と連続的な属性(中心性指標、年齢など)のいずれにも適用できる。計算方法の詳細は Farine (2014) を参照。
ここでは例として、再び毛づくろい頻度ネットワークgroom_mat_b(表2.5)を使用する。同類性はassortnetパッケージ(Farine, 2014)の関数群を用いて算出できる。
3.2.3.1 連続的な属性の場合
年齢が近い個体同士が結びつきやすいかを調べる。連続的な属性の同類性はassortment.continuous()関数で算出できる。係数は-0.397…となり、年齢の近い個体同士は結びつきにくいという結果になった。
## 年齢(2019年時点)
age <- c(13,10,11,11,15,8,13,9,7,18,9,11,16,11,14,11,11)
## 同類性
assortment.continuous(groom_mat_b,
## 各ノードの属性
vertex_values = age,
## 重みなしなら FALSE
weighted = TRUE)## $r
## [1] -0.3970963.2.3.2 離散的な属性の場合
同じ年齢カテゴリ(低順位: m、中順位: m、高順位: h)の個体同士が結びつきやすいかを調べる。離散的な属性の同類性はassortment.discrete()関数で算出できる。係数はかなり高く(0.484…)、同順位カテゴリ―の個体同士がよく結びつく傾向がある。
## 順位カテゴリ
rank <- c("m","m","l","l","h","h","h","h","h","h","l","l","l","m","m","m","m")
## 同類性
assortment.discrete(groom_mat_b,
## 各ノードの属性
types = rank,
## 重みなしなら FALSE
weighted = TRUE) -> assort_rank
assort_rank$r## [1] 0.4840036各カテゴリ間のノードのweightの合計を計算した隣接行列も出力してくれる(表3.5)。この表からも、同順位カテゴリ間での交渉が多いことが分かる。
assort_rank$mixing_matrix %>%
kable(digits = 2, align = "c",caption = "各カテゴリ間のweightの合計") %>%
kable_styling(font_size = 12, full_width = FALSE)| m | l | h | ai | |
|---|---|---|---|---|
| m | 0.25 | 0.08 | 0.06 | 0.40 |
| l | 0.08 | 0.13 | 0.02 | 0.23 |
| h | 0.06 | 0.02 | 0.28 | 0.36 |
| bi | 0.40 | 0.23 | 0.36 | 1.00 |
なお離散的な属性については、ANTsパッケージのmet.assortativity()関数を用いると、node permutation(詳細は4.2)で生成したランダムなネットワークにおける同類性を指定した数だけ生成してくれる。それらの何%より実際の同類性の数値が大きい/小さいかを検討することで、統計的な検定が行える。今回の例では、実測値はランダムな値の全てより小さいので、ランダムな場合より有意に小さいと言える(図3.11)。
## node label permutationで生成したランダムなネットワーク100個についてassortativityを算出
met.assortativity(groom_mat_b,
## 各ノードの固有ベクトル中心性
attr = rank,
## 重みなしの場合 FALSE
weighted = TRUE,
## node label permutationをするか
perm.nl = TRUE,
## permutationの数
nperm = 10000) -> nlperm_rank
### ランダムなassortativityの何%より小さい?
sum(nlperm_rank > assort_rank$r)/10000## [1] 1e-04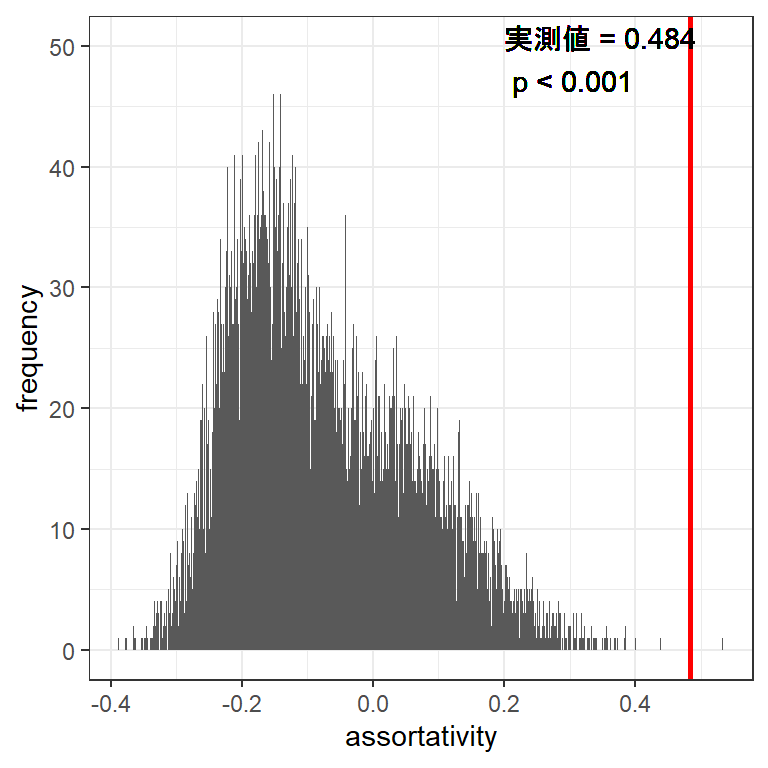
図3.11: ランダムなネットワークの同類性の分布(灰色)と実測値(赤)
3.2.4 推移性(Transitivity)
ネットワークにおいて、頂点\(i\)と\(j\)の間、および頂点\(j\)と\(k\)の間に関係があり、頂点\(i\)と\(k\)の間にも関係があるとき、関係が推移的であるという。例えば、図3.12で頂点A, B, Cの関係は推移的だが、頂点A, B, Gは推移的ではない。
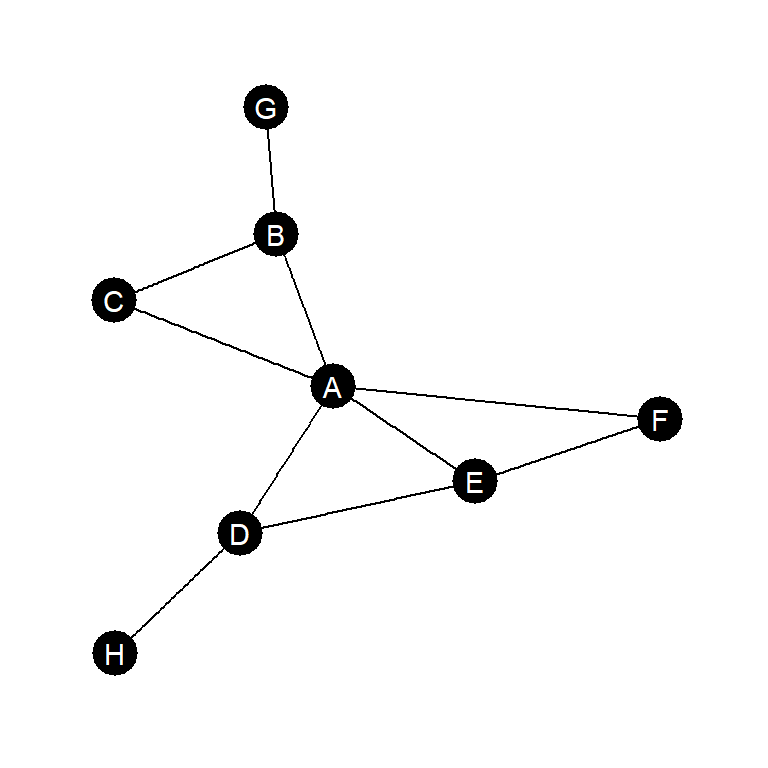
図3.12: 推移性の説明のための無向グラフの例
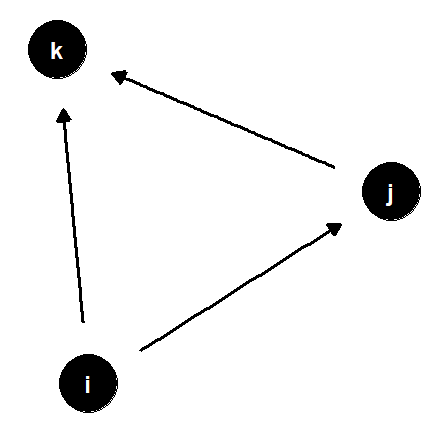
図3.13: 推移性の説明のための有向グラフの例
推移性はネットワーク内で推移的な関係が成り立っている比率を指す。例えば無向グラフの場合には、頂点\(i\)と\(j\)、\(j\)と\(k\)の間に辺があるとき、頂点\(i\)と\(k\)にも辺がある割合である。推移性はネットワークがどの程度クラスター化されているかの指標になる(Farine & Whitehead, 2015)。そのため、クラスター係数と呼ばれることもある。
例として、毛づくろい頻度ネットワークgroom_mat_b(表2.5)の推移性を算出する。推移性はigraphパッケージのtransitivity()関数で求められる。推移性は高い?
## [1] 0.69097223.2.5 Modularity
霊長類のネットワークの種間比較でよく用いられる指標にNewmanのmodularity(Newman, 2004; Whitehead, 2008)がある。この指標は、ネットワーク内を複数のクラスターに分けたとき、クラスター内の個体間での交渉がクラスター間の個体間の交渉よりどの程度多いかを示したもので、クラスターの数をcとするとき、-0.5~1-1/cの値をとる(Borgatti et al., 2022)。値が高いほどその差が大きいことを示し、クラスターの分け方が妥当であることを示す。Newman (2004) は、modularityが0.3以上のとき、クラスター間がよく分断されているとしている。例えばマカクの種間比較研究では、血縁ごとにクラスター分けしたとき、寛容性が低い種は高い種よりもmodularityが高い(0.33±0.08 vs 0.21 ±0.03)、つまり交渉がより血縁に偏っていることが分かっている(Sueur, Petit, et al., 2011)。
Modularityは以下のように定式化される(Csardi et al., 2006)。
\(Q = \frac{1}{2m} \sum_{i,j} (A_{ij} - \gamma \frac{k_i k_j}{2m}) \delta(c_i,c_j)\)
なお、\(m\)は辺の数、\(A_{ij}\)は隣接行列の\(i\)行目\(j\)列目の成分、\(k_i\)と\(k_j\)はノード\(i\)と\(j\)の重み付き中心性を表す(\(k_i\)と\(k_j\)に固有ベクトル中心性を使っている論文もある(Balasubramaniam et al., 2018))。また、\(\delta(c_i,c_j)\)はノード\(i\)と\(j\)が同じクラスターに属しているときは1、そうでないときは0になる。なお、\(\gamma \frac{k_i k_j}{2m}\)の部分は、ランダムに交渉が行割れていると仮定したときの\(A_{ij}\)の値である。\(\gamma\)はデフォルトでは1だが変化させることができ、大きい値をとるほどクラスター数が多くなる。
ここでは例として、毛づくろい頻度ネットワークgroom_mat_b(表2.5)を用いて、各順位カテゴリ内(低順位・中順位・高順位)の交渉がカテゴリ間の交渉よりどの程度多いかを、\(Q\)を算出することで求める。
Rでは、igraphパッケージのmodularity()関数で求めることができる。graph_from_adjacency_matrix()でigraphクラスに変換した後に算出する。また、weight =で明示的に各エッジのweightを与えてあげる必要があるよう。modularityは0.315…とそこそこ大きい値であるので、順位カテゴリ内に毛づくろいが偏っていることを示している。
## 順位カテゴリごとに番号を振る
rank <- c(2,2,1,1,3,3,3,3,3,3,1,1,1,2,2,2,2)
## igraphに変換
graph_groom <- graph_from_adjacency_matrix(groom_mat_b,
## 有向グラフなら "directed"
mode= "undirected",
## 重みなしなら NULL
weighted = TRUE)
modularity(graph_groom,
## クラスターの分け方
membership = rank,
## deltaの値
resolution = 1,
## 有向グラフなら TRUE
directed = FALSE,
## グラフのweightを与える
weights = E(graph_groom, directed = FALSE)$weight)## [1] 0.31529573.2.6 応用例(下位集団の検出)
ネットワーク内に下位集団(クラスター)が存在するかを調べる方法はたくさんあるが(詳細は 鈴木, 2017)、ここでは主に2つの方法に焦点を当てて紹介する。
3.2.6.1 Modularityを用いる方法
一つの方法としてmodularityが最大になるような分け方がある。igraphパッケージでは、cluster_optimal()でそのようなクラスタの分け方を算出してくれる。なお、ノード数が多い場合には時間がかかるため、様々な近似計算法が考案されている(cluster_fast_greedy()、cluster_walktrap()など)。
例として、毛づくろい頻度ネットワークgroom_mat_b(表2.5)について算出する。その結果、4つのクラスターに分類され、そのときのmodularityは0.40だった。概ね順位ごとに分かれていることが分かる(同じアルファベットから始まる個体が同一家系である)。高順位、中順位(2つに分かれている)、低順位にほぼ綺麗に分かれた。
## 算出
cluster_optimal(graph_groom,
weights = E(graph_groom)$weight) -> cluster_groom
## 結果
cluster_groom## IGRAPH clustering optimal, groups: 4, mod: 0.4
## + groups:
## $`1`
## [1] "Aka" "Ako" "Mei"
##
## $`2`
## [1] "Hen" "Hot" "Mal" "Mik" "Tam" "Tot"
##
## $`3`
## [1] "Kil" "Kit" "Koh" "Kor" "Kun" "Kur"
##
## $`4`
## + ... omitted several groups/vertices## [1] 0.4020546## 確認
modularity(graph_groom,
## クラスターの分け方
membership = membership(cluster_groom),
## deltaの値
resolution = 1,
## 有向グラフなら TRUE
directed = FALSE,
weights = E(graph_groom)$weight) ## [1] 0.4020546クラスターごとに色分けして図示すると図3.14のようになる。
set.seed(125)
graph_groom %>%
as_tbl_graph(directed = FALSE) %>%
## 各個体がどのクラスターに属するかを指定
mutate(member = as.factor(cluster_groom$membership)) %>%
ggraph(layout = "nicely")+
## クラスターごとに囲う
#geom_mark_hull(aes(x=x,y=y,fill = member),
# concavity = 10)+
geom_node_point(aes(color = member),shape = 16, size = 12)+
geom_edge_link(start_cap = circle(0.5,"cm"),
end_cap = circle(0.5,"cm"),
color = "grey55",
aes(width = weight))+
scale_edge_width(range = c(0,3))+
geom_node_text(aes(label = name), color = "white")+
theme_graph()+
scale_color_nejm()+
scale_fill_nejm()+
theme(aspect.ratio = 0.9)+
scale_x_continuous(expand = c(0.12,0.12))+
scale_y_continuous(expand = c(0.1,0.1))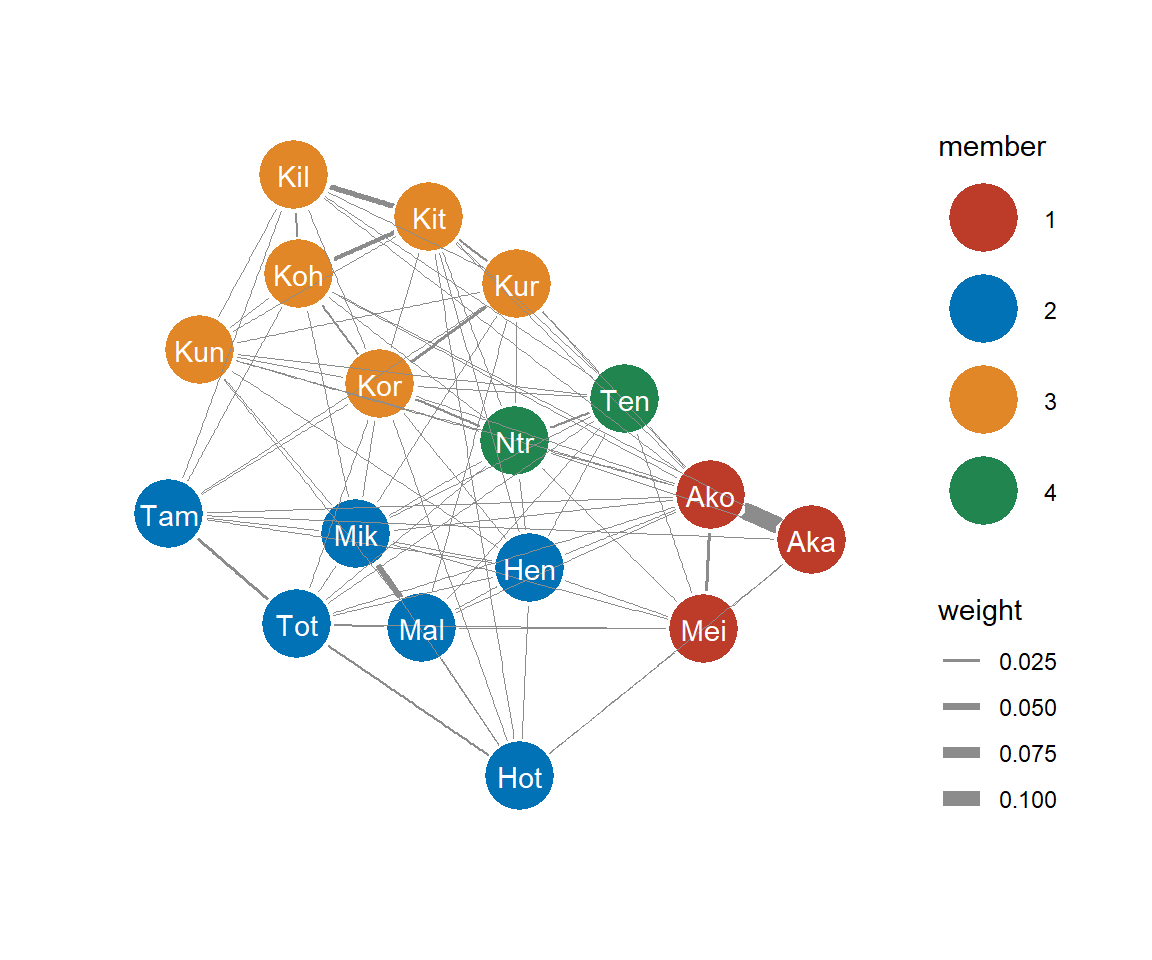
図3.14: Modularityに基づいてクラスターごとに色分けした毛づくろい頻度のグラフ
3.2.6.2 構造類似性を用いる方法
他の方法として、ノード間でネットワーク内での構造的な位置が類似している程度(= 構造類似性)を用いる方法がある。構造類似性の指標として良く用いられるのがユークリッド距離や相関係数である。このような構造類似性の指標を用い、ネットワーク上における位置の似た頂点をひとまとめにし、ネットワークをより少ないいくつかのブロック同士の関係に分けることをブロックモデリングという。
ユークリッド距離
ノード\(i\)と\(j\)のユークリッド距離(\(d_{ij}\))は隣接行列\(A = (a_{ij})\)について以下のように定式化される。\(d_{ij}\)が大きいほど類似性は低い。
\[
d_{ij} = \sqrt {\sum_{k =1}^{n}(a_{ij}-a_{jk})^2 + (a_{ki}-a_{kj})^2 }
\]
相関係数
ノード\(i\)とノード\(j\)の相関係数(\(r_{ij}\)は隣接行列\(A = (a_{ij})\)について以下のように定式化される。\(r_{ij}\)が大きいほど類似性は高い。
\[
r_{ij} = \frac{(i列とj列の共分散) + (i行とj行の共分散)}{(i列とi行の標準偏差) \times (j列とj行の標準偏差)}
\]
snaパッケージのequiv.clust()関数を用いることで、構造同値性に基づいたクラスター分析ができる。ここでは、毛づくろい頻度ネットワークgroom_mat_b(表2.5)のユークリッド距離を用いて分析を行う。method =で使用する構造類似性の指標を、clust.method =で階層クラスター分析の方法を指定する(方法の詳細はこちら) 。
## ユークリッド距離
cluster_groom_euc <- equiv.clust(groom_mat_b,
## 相関係数なら "correlation"
method = "euclidean",
## 階層クラスター分析の方法
cluster.method = "complete")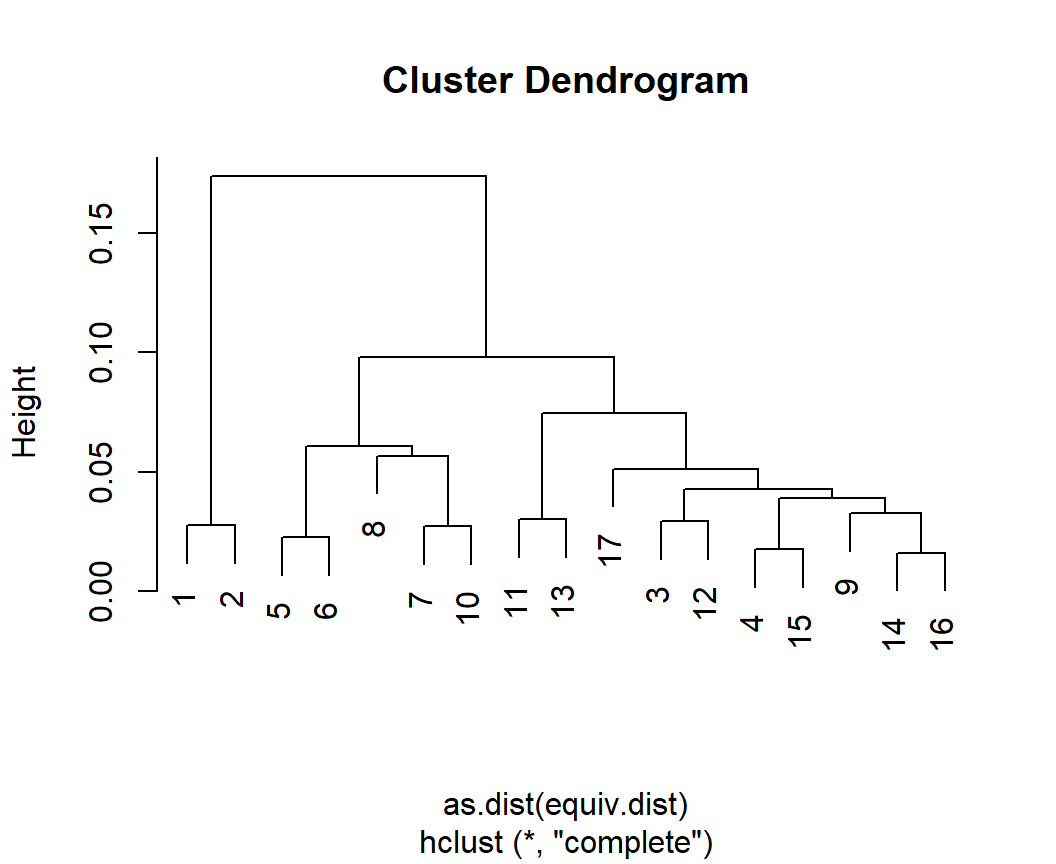
図3.15: クラスター分析結果に基づくデンドログラム
この結果からblockmodel()関数でブロックモデルを作る。引数h =でクラスター(= ブロック)を作る基準となる高さを、もしくは引数k =でブロック数を指定できる。ここでは、ブロック数を3つに指定したときの結果を調べる。各個体がどのブロックに振り分けられたかは、表3.7の通りである。
blockmodel_groom_3 <- blockmodel(## 隣接行列
groom_mat_b,
## クラスター分析結果
cluster_groom_euc,
## `k =`でクラスター数の指定。`h = `でクラスターの基準の高さも指定できる。
k = 3)
## メンバーシップ
data.frame(femaleID = blockmodel_groom_3$plabels,
block = blockmodel_groom_3$block.membership) %>%
arrange(femaleID) -> membership_3
membership_3 %>%
pivot_wider(names_from = femaleID, values_from = block) %>%
kable(align = "c", caption = "ブロック数が3のときに各個体が属するブロック") %>%
kable_styling(font_size = 8, full_width = FALSE)| Aka | Ako | Hen | Hot | Kil | Kit | Koh | Kor | Kun | Kur | Mal | Mei | Mik | Ntr | Tam | Ten | Tot |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 2 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
ブロック数を2から5に変化させたときにmodularityがどうなるかを調べたところ、k = 3のときに最大になるよう(表3.9)。
k = 2:5
## kを2~5にしたときに各個体が属するブロックを計算
map(k, ~blockmodel(## 隣接行列
groom_mat_b,
## クラスター分析結果
cluster_groom_euc,
## `k =`でクラスター数の指定。`h = `でクラスターの基準の高さも指定できる。
k = .)$block.membership) -> member_list
## modularityを算出
data.frame(k = rep(k,each = 17),femaleID = blockmodel_groom_3$plabels,
member = c(member_list[[1]],member_list[[2]],member_list[[3]],member_list[[4]])) %>%
group_by(k) %>%
nest() %>%
mutate(member2 = map(data,~arrange(., femaleID)$member)) %>%
select(k, member2) %>%
group_by(k) %>%
mutate(modularity = map(member2, ~modularity(graph_groom, membership = as.factor(.),
weights = E(graph_groom, directed = FALSE)$weight))) %>%
select(k, modularity) %>%
unnest(cols = c(modularity)) %>%
kable(align = "c", caption = "ブロック数を2~5にしたときのmodularity") %>%
kable_styling(font_size = 13, full_width = FALSE)| k | modularity |
|---|---|
| 2 | 0.2279996 |
| 3 | 0.3592285 |
| 4 | 0.3317726 |
| 5 | 0.2642927 |
clValidパッケージのclValid()関数では、様々な指標を用いてクラスター分けが妥当か算出してくれるよう。詳しくは、 Brock et al. (2008) もしくはこちらを参照。よく使用される指標であるDunn indexと silhouette widthの結果を見ると、3つのクラスターに分けるのが妥当だと示唆される。
clValid(obj = groom_mat_b,
nClust = 2:5,
clMethods = "hierarchical",
validation = "internal",
Metric = "euclidean") -> result
summary(result)##
## Clustering Methods:
## hierarchical
##
## Cluster sizes:
## 2 3 4 5
##
## Validation Measures:
## 2 3 4 5
##
## hierarchical Connectivity 2.9290 5.8579 8.8869 11.9270
## Dunn 0.8946 1.3325 0.6119 0.6219
## Silhouette 0.5547 0.5632 0.2284 0.1967
##
## Optimal Scores:
##
## Score Method Clusters
## Connectivity 2.9290 hierarchical 2
## Dunn 1.3325 hierarchical 3
## Silhouette 0.5632 hierarchical 33つのクラスターごとに色分けして図示すると図3.16のようになる。
set.seed(125)
graph_groom %>%
as_tbl_graph(directed = FALSE) %>%
## 各個体がどのブロックに属するかを指定
mutate(member = as.factor(membership_3$block)) %>%
ggraph(layout = "nicely")+
## ブロックごとに囲む
#geom_mark_hull(aes(x=x,y=y,fill = member),
# concavity = 10)+
geom_node_point(aes(color = member),shape = 16, size = 12)+
geom_edge_link(start_cap = circle(0.5,"cm"),
end_cap = circle(0.5,"cm"),
color = "grey55",
aes(width = weight))+
scale_edge_width(range = c(0,3))+
geom_node_text(aes(label = name), color = "white")+
theme_graph()+
scale_color_nejm()+
scale_fill_nejm()+
theme(aspect.ratio = 0.9)+
scale_x_continuous(expand = c(0.1,0.1))+
scale_y_continuous(expand = c(0.1,0.1))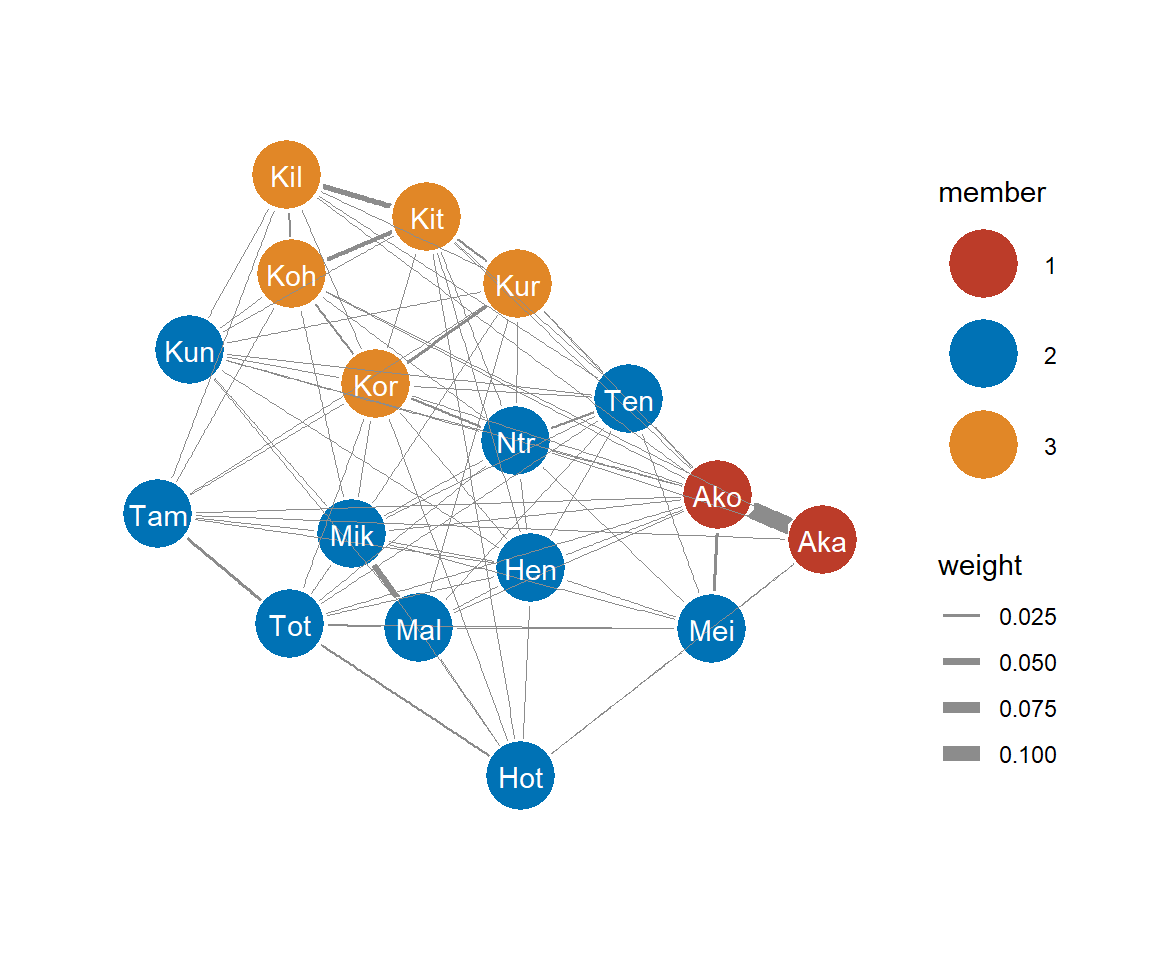
図3.16: 構造類似性に基づいてクラスターごとに色分けした毛づくろい頻度のグラフ