3.1 ノードについての諸指標(中心性指標)
ここでは、各ノードのネットワーク内での特性を表す指標についてまとめる。中心性指標は、いずれもあるノードがそのグラフでどのくらい「中心的」であるかを表す指標である。以下で見るように、中心性を評価する方法は数多く提案されている。
基本的には、いずれもANTsパッケージのmet.*()関数で出力できる(*には中心性指標の名前)。これらの関数は、各ノードについて算出した中心性を各ノードの属性データ(例えば年齢や順位など)を記したデータフレームに追加していってくれるので、分析を行う際に非常に便利である。
属性データの例(年齢と順位)
attr <- data.frame(name = c("A","B","C","D","E","F","G","H"),
age = c(12,13,12,11,14,15,18,9),
rank = c(2,3,4,1,8,1,7,6))
attr %>%
datatable(rownames = FALSE, width = "55%")3.1.1 近接中心性(closeness centrality)
グラフの「中心」のイメージとしてよく思い浮かぶのは、「他のノードとの距離が小さいノードほどより中心的である」というものである。近接中心性は他のノードとの最短距離の合計が小さいほど大きくなる中心性指標で、以下のように定式化され、0から1の値をとる。
\[ C_c(i) = \frac{n-1}{\sum_{j=1}^n d_{ij}} \]
なお\(n\)はノード数で、\(d_{ij}\)はノード\(i\)から\(j\)に最短で到達するために通る辺の数(= 最短距離)である。例えば、以下のグラフ(図3.1)において、AからHへの最短距離は2、GからHへの最短距離は4である。分子に\(n-1\)があるのは、最大値が1になるようにするためである。
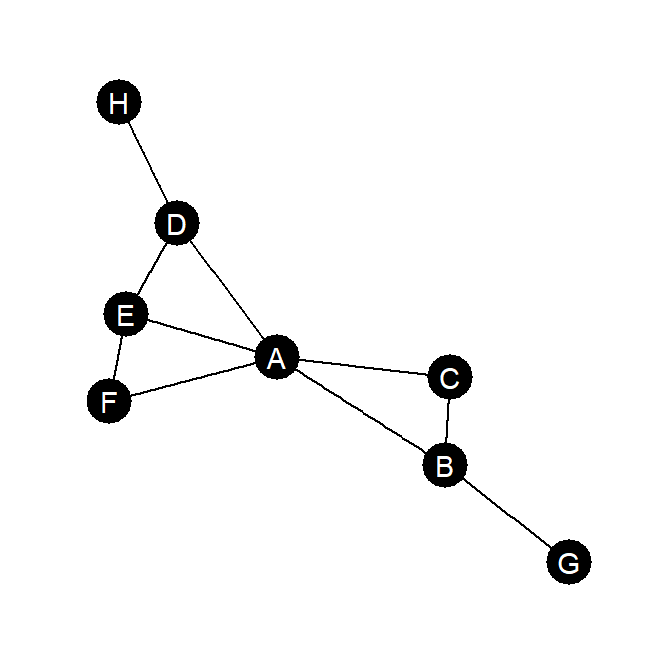
図3.1: 近接中心性算出のための無向グラフの例
例として図3.1のグラフの各ノードの近接中心性を求める。Rでは基本的に隣接行列の形でデータを扱うことが多い。今回も中心性指標の算出のため、図3.1の隣接行列を以下のように作成する。
mat_undir <- matrix(c(0,1,1,1,1,1,0,0,
1,0,1,0,0,0,1,0,
1,1,0,0,0,0,0,0,
1,0,0,0,1,0,0,1,
1,0,0,1,0,1,0,0,
1,0,0,0,1,0,0,0,
0,1,0,0,0,0,0,0,
0,0,0,1,0,0,0,0),
nrow = 8, ncol = 8)
colnames(mat_undir) <- c("A","B","C","D","E","F","G","H")
rownames(mat_undir) <- c("A","B","C","D","E","F","G","H")近接中心性はsnaパッケージのcloseness()関数で求められる。ノードAの中心性の値が最も高いことが分かる。
sna::closeness(mat_undir,
## 有向グラフなら "digraph"
gmode = "graph",
## 重み付きグラフなら FALSE
ignore.eval = TRUE)## [1] 0.7777778 0.5833333 0.5384615 0.5833333 0.5833333 0.5000000 0.3888889
## [8] 0.38888893.1.2 次数中心性(Degree centrality)
最も簡便で適用範囲の広い中心性が次数中心性である(鈴木, 2017)。重みなしグラフについて算出でき、各ノードに辺で接続しているノードの数を、そのノードの次数中心性とする。例えば、図3.1では、Aの次数中心性は5、Dの次数中心性は3である。
例として、図3.1の次数中心性を求める。ANTsパッケージでは、met.degree()関数で求められる。以下のようにdf =に属性が入ったデータフレームを指定することで、算出した次数中心性をそのデータフレームに追加してくれる。
met.degree(mat_undir,
## 属性データフレーム
df = attr,
## 個体IDの列番号
dfid = 1) %>%
kable(align = "c") %>%
kable_styling(font_size = 12, full_width = FALSE)| name | age | rank | degree |
|---|---|---|---|
| A | 12 | 2 | 5 |
| B | 13 | 3 | 3 |
| C | 12 | 4 | 2 |
| D | 11 | 1 | 3 |
| E | 14 | 8 | 3 |
| F | 15 | 1 | 2 |
| G | 18 | 7 | 1 |
| H | 9 | 6 | 1 |
有向グラフでは、他のノードから入ってくる辺の数である入次数(indegree)と他のノードへ入っていく辺の数である出次数(outdegree)が区別される。図3.2では、Aの入次数は2、出次数は3である。
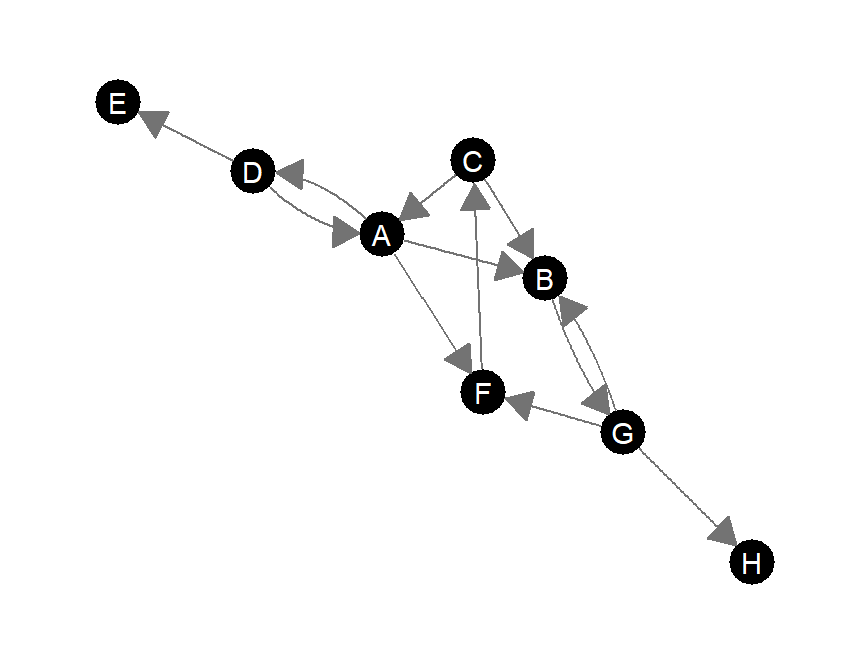
図3.2: 次数中心性算出のための有向グラフの例
ANTsパッケージでは、それぞれmet.indegree()とmet.outdegree()で求められる。
## このようにすれば、2つの中心性指標を共に属性データに結合できる。
met.indegree(
## 隣接行列
mat_dir,
## 属性データフレーム
df = attr,
## 個体IDの列番号
dfid = 1) -> attr_b
met.outdegree(mat_dir,
## 属性データフレーム(入次数の情報も含む)
df = attr_b,
## 個体IDの列番号
dfid = 1) %>%
kable(align = "c") %>%
kable_styling(font_size = 12, full_width = FALSE)| name | age | rank | indegree | outdegree |
|---|---|---|---|---|
| A | 12 | 2 | 2 | 3 |
| B | 13 | 3 | 3 | 1 |
| C | 12 | 4 | 1 | 2 |
| D | 11 | 1 | 1 | 2 |
| E | 14 | 8 | 1 | 0 |
| F | 15 | 1 | 2 | 1 |
| G | 18 | 7 | 1 | 3 |
| H | 9 | 6 | 1 | 0 |
3.1.3 重み付き中心性(Strength centrality)
重み付き中心性は、各ノードに接続している辺の重みの合計で表される中心性である。図3.3は表3.1の隣接行列(mat_undir_b)のグラフである。グラフの辺上の数字は重みを表す。このとき、Aの重み付き中心性は\(3 + 2+ 2+ 1 +1=9\)、Cの重み付き中心性は\(3 + 2 = 5\)である。
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 2 | 3 | 1 | 2 | 1 | 0 | 0 |
| B | 2 | 0 | 2 | 0 | 0 | 0 | 1 | 0 |
| C | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 1 |
| E | 2 | 0 | 0 | 3 | 0 | 2 | 0 | 0 |
| F | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 |
| G | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
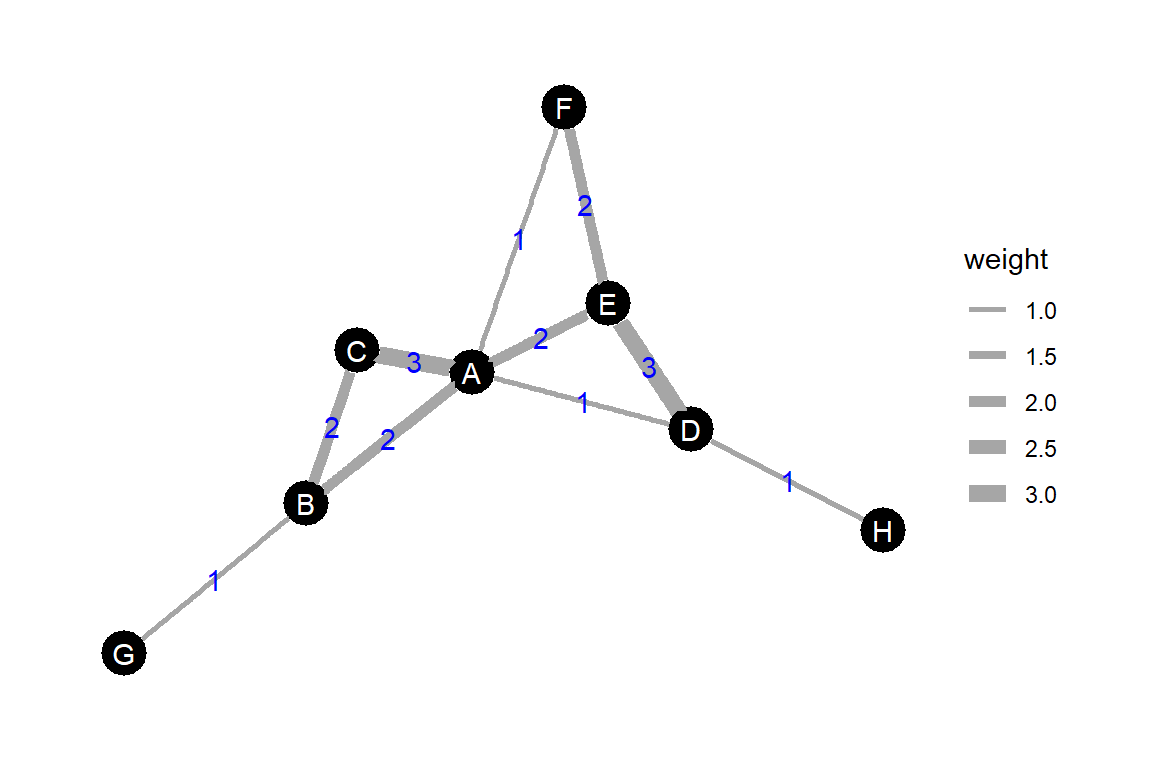
図3.3: 重み付き中心性算出のための無向グラフの例
ANTsパッケージでは、met.strength()で求められる。まお、ANTsパッケージでは常に有向グラフとして計算されてしまうようなので、1/2してあげる必要がある。
met.strength(mat_undir_b/2,
## 属性データフレーム
df = attr,
## 個体IDの列番号
dfid = 1) %>%
kable(align = "c") %>%
kable_styling(font_size = 12, full_width = FALSE)| name | age | rank | strength |
|---|---|---|---|
| A | 12 | 2 | 9 |
| B | 13 | 3 | 5 |
| C | 12 | 4 | 5 |
| D | 11 | 1 | 5 |
| E | 14 | 8 | 7 |
| F | 15 | 1 | 3 |
| G | 18 | 7 | 1 |
| H | 9 | 6 | 1 |
なお、有向データについては次数中心性と同じようにinstrengthとoutstrengthで区別することもできる。その場合は、それぞれANTsパッケージのmet.indegree()とmet.outstrength()で算出できる。
おまけ
snaパッケージでは、次数中心性と重み付き中心性を全てdegree()関数で求められる。
sna::degree(mat_undir_b,
## 重みなしの場合 TRUE
ignore.eval = FALSE,
## 有向グラフの場合は "digraph",
gmode = "graph",
## indegreeの場合は "indegree"、outdegreeの場合は"outdegree",
cmode = "freeman")## [1] 9 5 5 5 7 3 1 13.1.4 固有ベクトル中心性(Eigenvector centrality)
次数中心性や重み付け中心性は、あるノードに接続する辺の数や重みの合計に基づく中心性指標であった。つまり、例えば毛づくろい頻度ネットワークでは、多くの個体と毛づくろいしている個体や、毛づくろい頻度の合計が多い個体の中心性が高く評価される。しかし、この方法は中心性を評価する指標として適切ではない場合がある。例えば、毛づくろいを通してある行動がネットワーク内をどのように伝播するかを考えるとき、毛づくろい相手の多い個体と毛づくろいすることは、毛づくろい相手の少ない個体と毛づくろいするよりも高く評価するべきかもしれない。
このことを考慮するためは、あるノードの中心性を評価するときに、そのノードと繋がっているノードの中心性の大きさを反映させる必要がある。例えば、あるノードの中心性がそれとつながるノードの中心性の和に比例する方法が考えられる。このとき、ある無向グラフの隣接行列を\(A = (a_{ij})\)とし、そこに含まれるノードの中心性を成分とする列ベクトルを\(c=c_i\)とすると、ノード\(i\)の中心性\(c_i\)は次のように表現できる。ただし、\(\lambda\)は正の比例定数である。
\[ \begin{aligned} c_i &= \frac{1}{\lambda} \sum_{j=1}^{n} a_{ij}c_j \end{aligned} \]
行列とベクトルで表すと、以下のように書ける。
\[
\begin{aligned}
c &= \frac{1}{\lambda} Ac\\
\therefore \lambda c &= Ac
\end{aligned}
\]
例えば、4個体について以下の隣接行列\(A\)と中心性を成分とするベクトル\(c\)を考える。
\[ \begin{aligned} &A = (a_{ij}) = \begin{pmatrix} 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0\\ \end{pmatrix}\\ \\ &c = \begin{pmatrix} c_1\\ c_2\\ c_3\\ c_4 \end{pmatrix} \end{aligned} \]
このとき、以下のような式を満たす\(c\)と\(\lambda\)を求めることになる。
\[ \begin{aligned} \lambda \begin{pmatrix}c_1\\ c_2\\ c_3\\ c_4 \end{pmatrix} &= \begin{pmatrix} 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0 \end{pmatrix} \begin{pmatrix} c_1\\ c_2\\ c_3\\ c_4\\ \end{pmatrix}\\ \\ \therefore \lambda \begin{pmatrix} c_1\\ c_2\\ c_3\\ c_4\\ \end{pmatrix} &= \begin{pmatrix} c_2\\ c_1 +c_3+ c_4\\ c_2+c_4\\ c_2+c_3\\ \end{pmatrix} \end{aligned} \]
ここで、これを満たす\(\lambda\)は正方行列\(A\)の固有値、\(c\)は固有ベクトルになる1。つまり、隣接行列の固有ベクトルを求めれば、隣接するノードの中心性を反映した中心性を求めることができる(なお、固有値と固有ベクトルの組み合わせは\(A\)の列数と同じだけある)。特に絶対値が最大となる固有値に対応する第1固有ベクトルを中心性指標としたものを、固有ベクトル中心性(eigenvector centrality)という。
あるノードの固有ベクトル中心性は、そのノードにつながるノードの中心性を反映しているが、それらのノードは更にそれらにつながるノードの中心性を反映している。このように、固有ベクトル中心性は、そのノードから辺をたどって到達できるすべてのノードの中心性を反映している。
先ほどの例の\(A\)の第1固有ベクトルは以下のように求められる。固有ベクトルは負の値をとることもあるため、絶対値をとることが多い。また、最大値を1とした比で表すことも多い。
A = matrix(c(0,1,0,0,
1,0,1,1,
0,1,0,1,
0,1,1,0),
nrow = 4, byrow = TRUE)
## 第1固有ベクトル。絶対値をとる。
evc <- abs(eigen(A)$vectors[,1])
## 最大値を1とするようにする
evc/max(evc)## [1] 0.4608111 1.0000000 0.8546377 0.8546377ANTsパッケージではmet.eigen()関数で、snaパッケージではevcent()関数で固有ベクトル中心性を求められる。前者は最大が1になるように変形しているのに対し、後者はそのような変形はしていない(定数倍しただけなので、分析上はどちらでも構わない)。
## [1] 0.4608111 1.0000000 0.8546377 0.8546377## [1] 0.2818452 0.6116285 0.5227207 0.5227207以上は重みなしグラフについて算出を行ったが、重み付きグラフについても同様に算出できる。
隣接行列mat_undir_b(表3.1)ついて、それぞれ重み付き中心性(左)と固有ベクトル中心性(右)の値をノードの大きさに反映させたグラフが図3.4である。
set.seed(123)
## 重み付き中心性の算出
met.strength(mat_undir_b/2,
df = attr,
dfid = 1) -> attr_st
## 固有ベクトル中心性の算出
met.eigen(mat_undir_b,
df = attr_st,
dfid = 1) -> attr_st_evc
## 重み付き中心性のグラフ
mat_undir_b %>%
as_tbl_graph(directed = FALSE) %>%
## `tbl_graph`に重み付き中心性の情報を追加
mutate(strength = attr_st_evc$strength) %>%
ggraph(layout = "nicely")+
geom_node_point(aes(size = strength), shape = 16, color = "black")+
scale_size(range = c(6,13))+
geom_edge_link(aes(width = weight),color = "grey65",
end_cap = circle(0.5,"cm"),
start_cap = circle(0.5,"cm"))+
geom_node_text(aes(label = name), color = "white")+
scale_edge_width(range = c(1,3))+
labs(title = "重み付き中心性")+
theme_graph() -> p_strength
## 固有ベクトル中心性のグラフ
mat_undir_b %>%
as_tbl_graph(directed = FALSE) %>%
## `tbl_graph`に固有ベクトル中心性の情報を追加
mutate(eigen = attr_st_evc$eigen) %>%
ggraph(layout = "nicely")+
geom_node_point(aes(size = eigen), shape = 16, color = "black")+
scale_size(range = c(6,13))+
geom_edge_link(aes(width = weight),color = "grey65",
end_cap = circle(0.5,"cm"),
start_cap = circle(0.5,"cm"))+
geom_node_text(aes(label = name), color = "white")+
scale_edge_width(range = c(1,3))+
labs(title = "固有ベクトル中心性")+
theme_graph() -> p_eigen
p_strength + p_eigen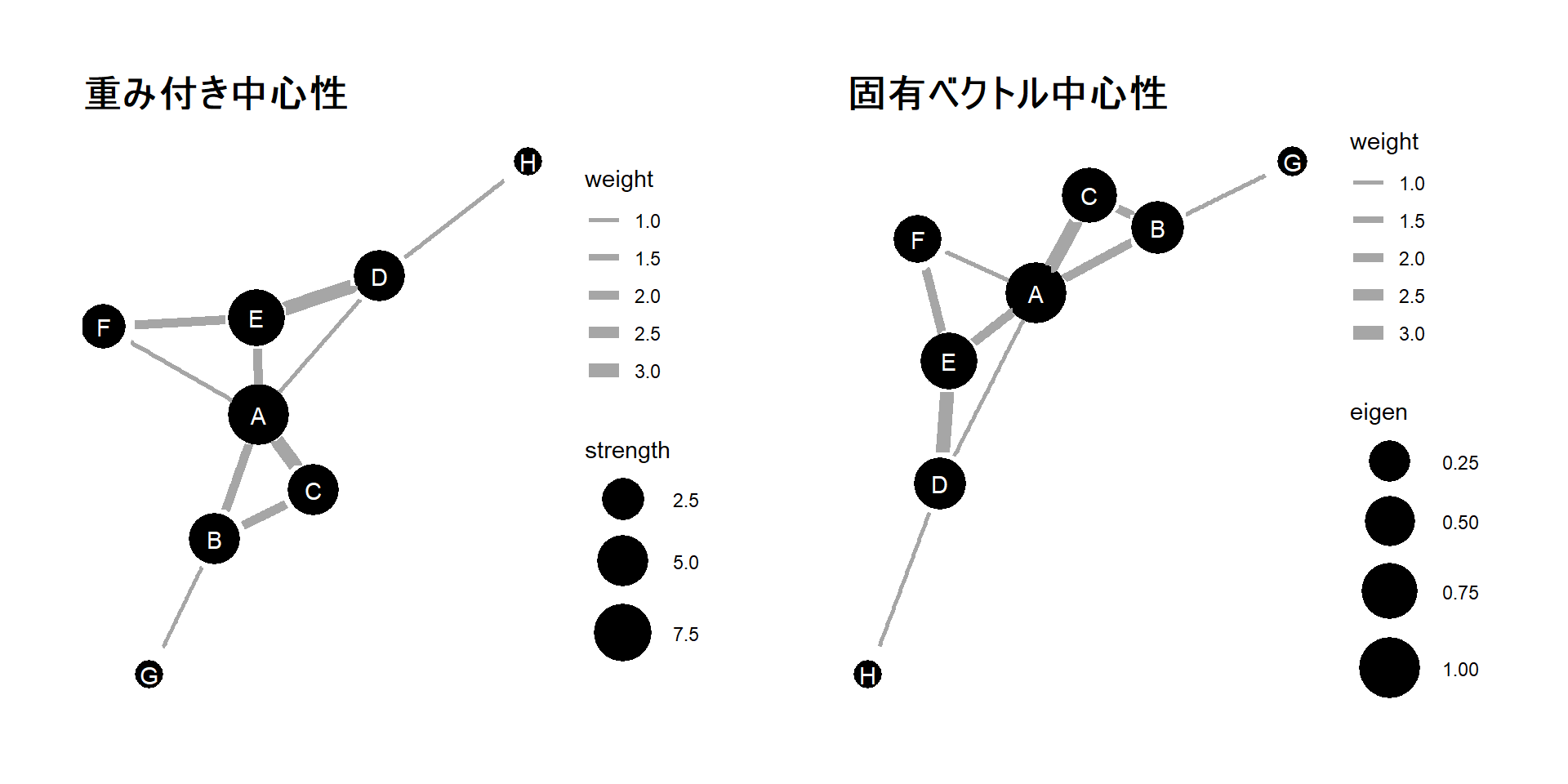
図3.4: 重み付き中心性(左)と固有ベクトル中心性(右)の値をノードの大きさに反映させたグラフ
固有ベクトル中心性は、有向グラフにも適用できるよう。各個体のinstrengthとoutstrengthに着目することで、それぞれineigenとouteigenが算出できる。それぞれの説明についてはこちらのサイトを参照。
一般的に、以下のようになるよう。
ineigen: 他の個体からよく毛づくろいされる個体からよく毛づくろいされるとき、ineigenが大きくなる。
outeigen: 他の個体をよく毛づくろいする個体にたくさん毛づくろいするとき、outeigenが大きくなる。
例えば、第2章で算出した表2.3の隣接行列(groom_mat)のineigenとouteigenは、ANTsパッケージを用いて以下のように求められる。
## 属性テーブル
df <- data.frame(femaleID = colnames(groom_mat))
## ineigen
met.eigen(groom_mat,
df = df,
dfid = 1,
## 重みなしの場合はFALSE
binary = FALSE,
## 無効グラフの場合はTRUE
sym = FALSE,
## outeigenの場合はTRUE
out = FALSE
) -> df
## outeigen
met.eigen(groom_mat,
df = df,
dfid = 1,
## 重みなしの場合はFALSE
binary = FALSE,
## 無効グラフの場合はTRUE
sym = FALSE,
## ineigenの場合はFALSE
out = TRUE
) -> dfそれぞれineigen(左)とouteigen(右)の値をノードの大きさに反映させたグラフが図3.5である。
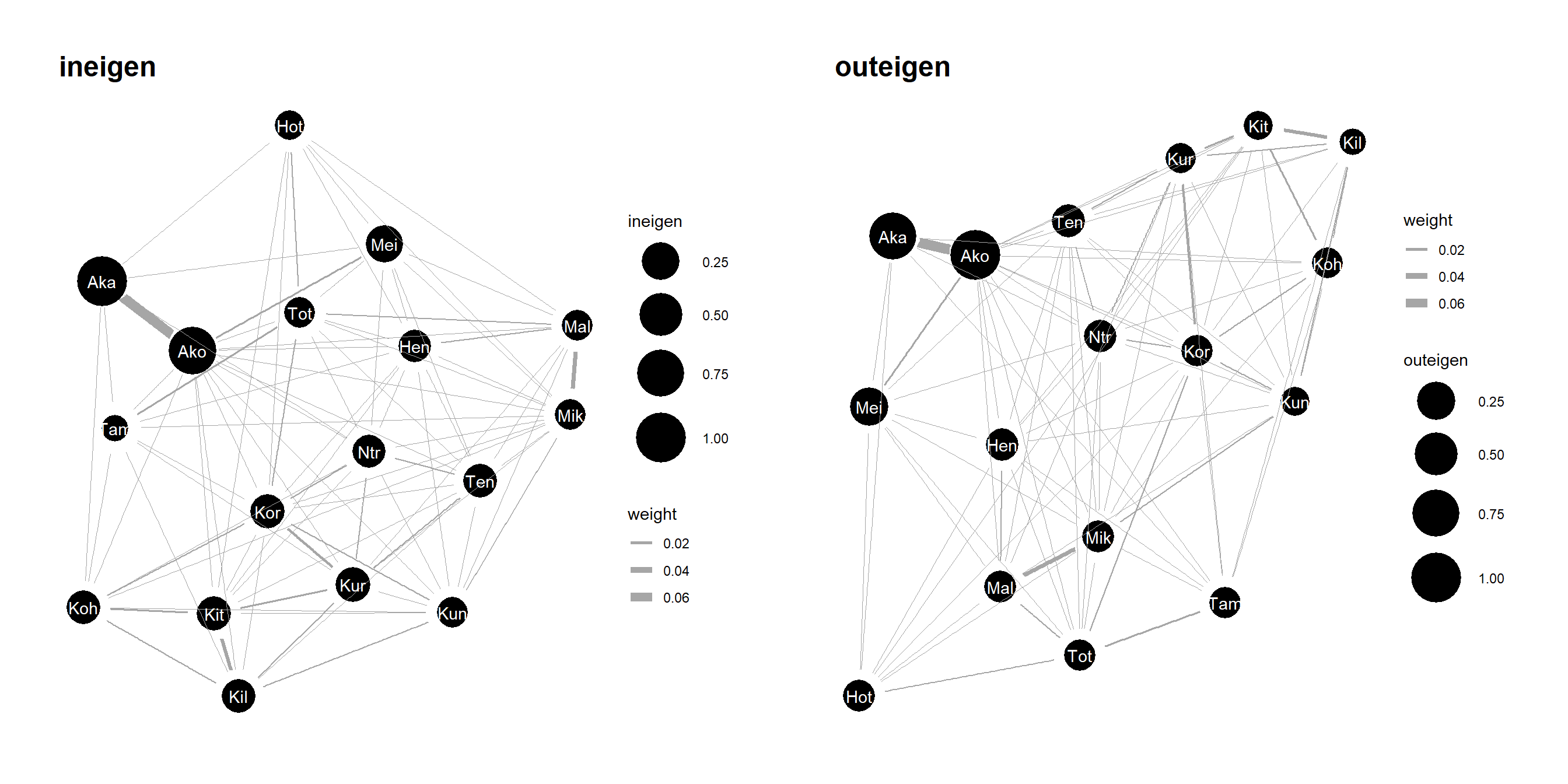
図3.5: ineigen(左)とouteigen(右)の値をノードの大きさに反映させたグラフ
3.1.5 PageRank
固有ベクトル中心性は、分離したグラフや有向グラフの中心性分析には使いにくい。PageRankは固有ベクトルに基づきながら、これらのグラフにも適用できる中心性指標である。もともとはウェブページの評価法として、Google創業者であるラリー・ペイジとセルゲイ・ブリンらによって開発され(Page et al., 1999)、他ページからのリンクが多いページほどランキングが高く、ランキングの高いページからのリンクや、他のページへのリンクが少ないページからのリンクを高く評価するというアルゴリズムに従う。詳細な算出方法は複雑なので、ここでは説明しない。詳しくは 鈴木 (2017) を参照。
PageRankはigraphパッケージを用いて算出できる。表3.3の隣接行列(mat_dir_b)のPageRankを算出する。
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 2 | 0 | 1 | 0 | 1 | 0 | 0 |
| B | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 |
| C | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| E | 2 | 0 | 0 | 3 | 0 | 0 | 0 | 0 |
| F | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 |
| G | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| H | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
igraphパッケージでデータを扱う際には、まず隣接行列をigraphクラスにしなくてはならない。graph_from_adjacency_matrix()関数でigraphクラスに変換した後、page.rank()関数でPageRankを算出する。
mat_dir %>%
## 隣接行列をgraphに変換
graph_from_adjacency_matrix(weighted = NULL, mode = "directed") %>%
## PageRankの算出
page.rank(directed = TRUE) -> page_rank
page_rank$vector## A B C D E F G
## 0.12584798 0.18619542 0.14217932 0.07093242 0.06542177 0.12576921 0.19354160
## H
## 0.09011228PageRankの値をノードの大きさに反映したグラフが図3.6である。
set.seed(123)
mat_dir_b %>%
as_tbl_graph(directed = TRUE) %>%
## `tbl_graph`にPageRankの情報を追加
mutate(PageRank = page_rank$vector) %>%
ggraph(layout = "nicely")+
geom_node_point(aes(size = PageRank),shape = 16, color = "black")+
scale_size(range = c(6,13))+
geom_edge_fan(aes(width = weight),
color = "grey65",
arrow = arrow(angle = 30, length = unit(4,units = "mm"), type = "closed"),
end_cap = circle(0.5,"cm"),
start_cap = circle(0.5,"cm"))+
geom_node_text(aes(label = name), color = "white")+
scale_edge_width(range = c(0,2))+
labs(title = "PageRank")+
theme_graph()+
scale_x_continuous(expand = c(0.05,0.05))+
scale_y_continuous(expand = c(0.05,0.05))-> p_pr
p_pr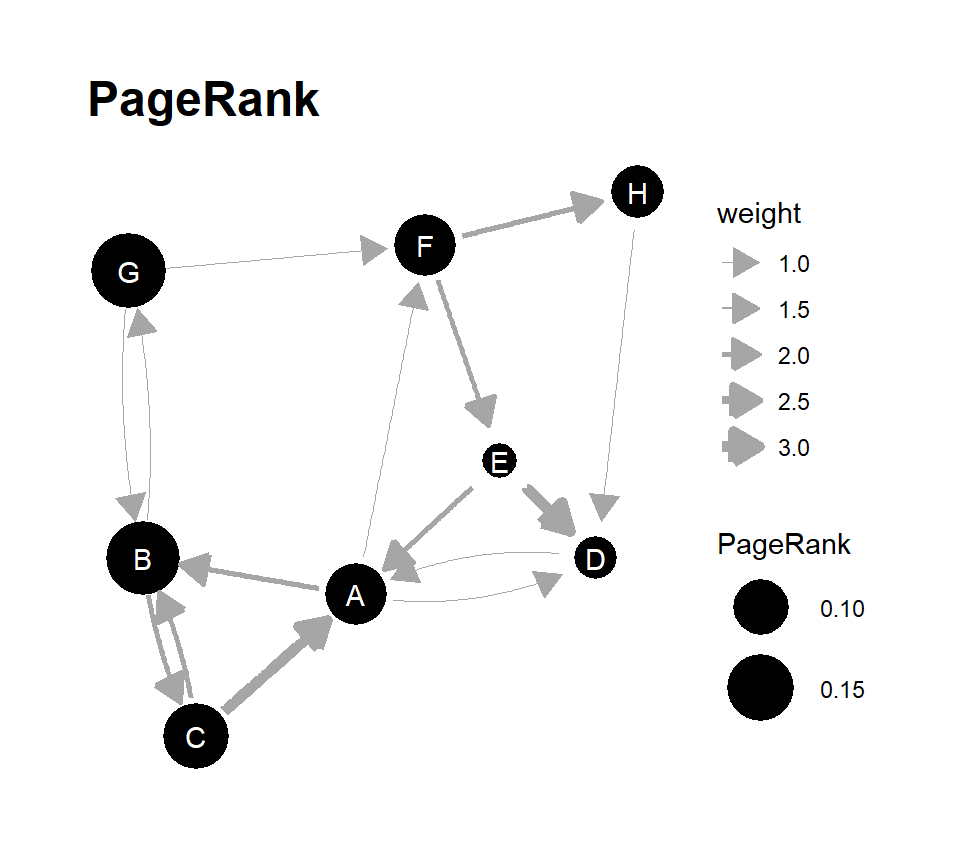
図3.6: PageRankの値をノードの大きさに反映させたグラフ
3.1.6 媒介中心性(Betweeness centrality)
ネットワークにおける媒介や伝達に着目した中心性に媒介中心性がある。媒介中心性は、他のノード同士をつなぐ最短経路上に位置するノードは、ノード間の仲介や情報の伝達に与える影響が大きいという点で有力であり、より多くのノード間の最短経路上にあるノードほどその影響力が大きいとする指標である。
ノード\(i\)の媒介中心性は以下の式で定式化される。なお、\(g_{jk}\)はノード\(j\)と\(k\)の間の最短経路数であり、\(g_{ij}(i)\)はノード\(j\)と\(k\)の間の最短経路のうちノード\(i\)を通るものの数である。無向グラフの場合、\(j < k\)である。
\[
C_b(i) = \sum_{i \neq j \neq k} \frac {g_{jk}(i)}{g_{jk}}
\]
ANTsパッケージではmet.betweeness()関数で、snaパッケージではsna::betweeness()関数で媒介中心性を求められる。表3.3の隣接行列(mat_dir_b)について算出すると、以下のようになる。
## ANTs
met.betweenness(mat_dir_b,
## 重みなしならTRUE
binary = FALSE,
## 無向グラフならTRUE
sym = FALSE,
## 最も重みの合計が高い経路を最短とする
shortest.weight = TRUE,
df = attr,
dfid = 1) %>%
kable(align = "c") %>%
kable_styling(font_size = 12, full_width = FALSE)| name | age | rank | norm.short.outbetweenness |
|---|---|---|---|
| A | 12 | 2 | 22.0 |
| B | 13 | 3 | 13.5 |
| C | 12 | 4 | 1.0 |
| D | 11 | 1 | 8.5 |
| E | 14 | 8 | 2.5 |
| F | 15 | 1 | 15.0 |
| G | 18 | 7 | 5.5 |
| H | 9 | 6 | 5.5 |
## sna
sna::betweenness(mat_dir_b,
## 無向グラフなら"undirected"
cmode = "directed",
## 重みなしならTRUE
ignore.eval = FALSE)## [1] 22.0 13.5 1.0 8.5 2.5 15.0 5.5 5.5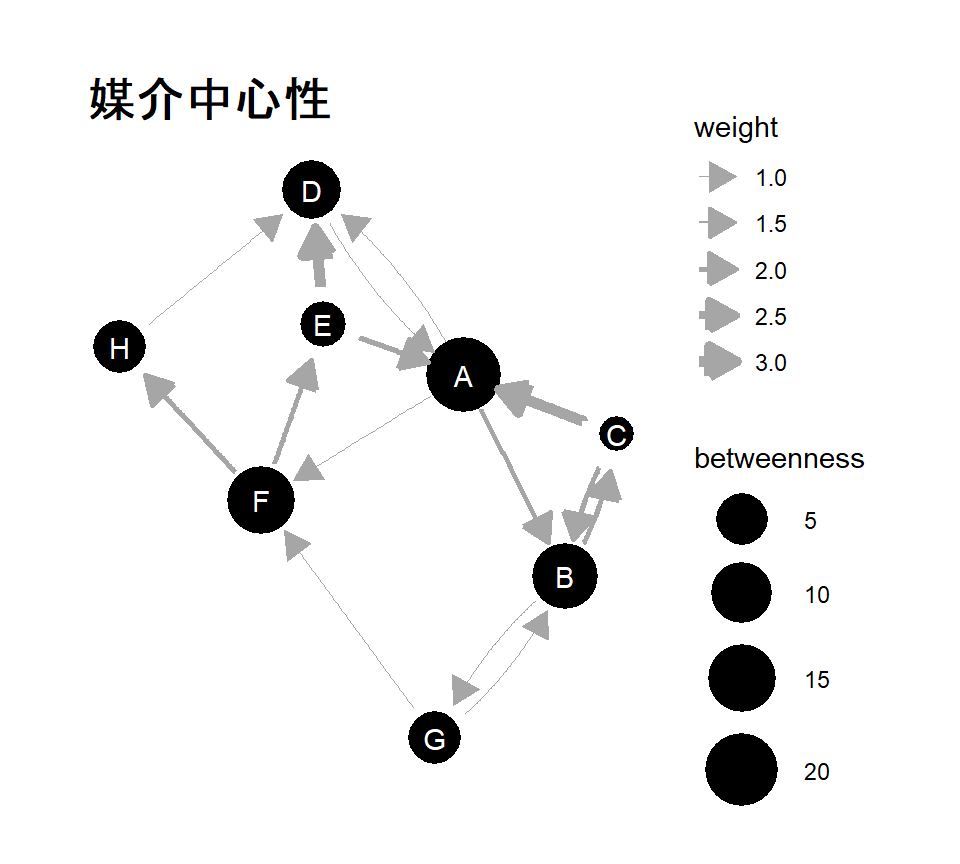
図3.7: 媒介中心性の値をノードの大きさに反映させたグラフ
3.1.7 情報中心性(Information centrality)
媒介中心性は最短経路以外の経路や、経路の長さを考慮していなかった。しかし、実際の情報の伝達は最短経路のみでなされるとは限らないし、情報伝達に関わる人が多いほど情報の精度が下がるような可能性もある。そこで、ノード間の最短経路以外の経路や経路の長さを考慮した指標として、情報中心性が考案された。
情報中心性の算出では、経路が短いほど高く評価されるように経路の長さの逆数で重みづけされる。例えば、図3.8のノード\(2\)と\(4\)について考える。これらのノードの間の経路には\(2-1-4\)と\(2-3-1-4\)の2通りがあり、それぞれの長さは2と3である。ただし、2つの経路には\(1-4\)という共通の経路が存在する。
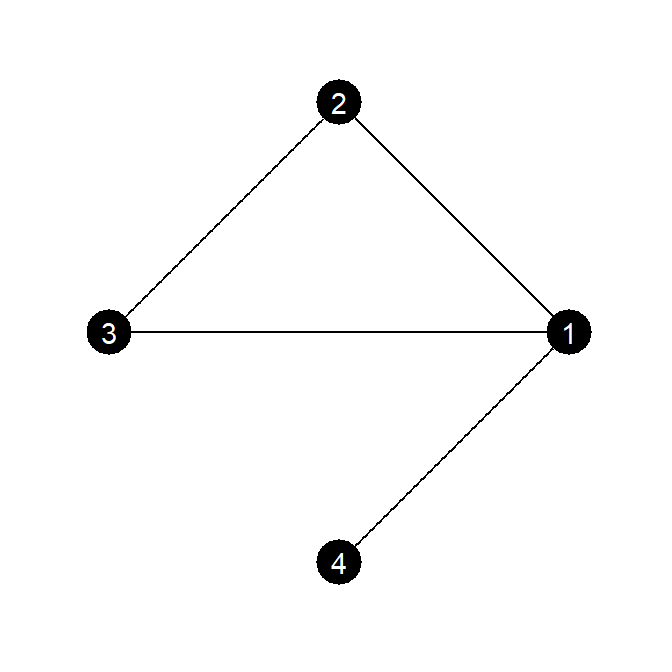
図3.8: 情報中心性算出のための無向グラフの例
このとき、ノード\(2\)と\(4\)について以下の行列\(D_{24}\)を考える。なお、行列の対角成分にはそれぞれの経路の長さが、それ以外の成分には2つの経路で共通する辺の数が入る。
\(D_{24} = \begin{pmatrix} 2 & 1 \\1 & 3\end{pmatrix}\)
そして、この行列の逆行列2\(D_{24}^{-1}\)の各行の成分の合計を、各経路の情報量とする。この場合、\(0.6-0.2 = 0.4\)が経路\(2-1-4\)の、\(-0.2 + 0.4 = 0.2\)が経路\(2-3-1-4\)の情報量である。また、その和(\(0.4+0.2=0.6\))をノード\(2\)と\(4\)のペアについての情報量(\(I_{24}\))とする。このように全てのノードペアについての情報量を算出する(自身との情報量は\(I_{ii} = \infty\)である)。
\(D_{24}^{-1} = \begin{pmatrix} 0.6 & -0.2 \\ -0.2 & 0.4 \end{pmatrix}\)
このとき、各ノード\(i\)の情報中心性(\(C_{inf}(i)\))は、ノード\(i\)が含まれるノードペアの情報量の調和平均3になる。数式では以下のように書ける。ただし、\(n\)は全ノードの数である。
\(C_{inf}(i) = \frac{n}{\sum_{j=1}^n 1/I_{ij}}\)
情報中心性はsnaパッケージのinfocent()関数で求められる。表3.3の隣接行列(mat_dir_b)について算出すると、以下のようになる。
## [1] 1.881874 1.408537 1.157895 1.439252 1.483146 1.714286 1.200000 1.168142情報中心性の値をノードの大きさに反映したグラフを、それぞれPageRankと媒介中心性の値をノードの大きさに反映した2つのグラフと並べたものがが図3.9である。
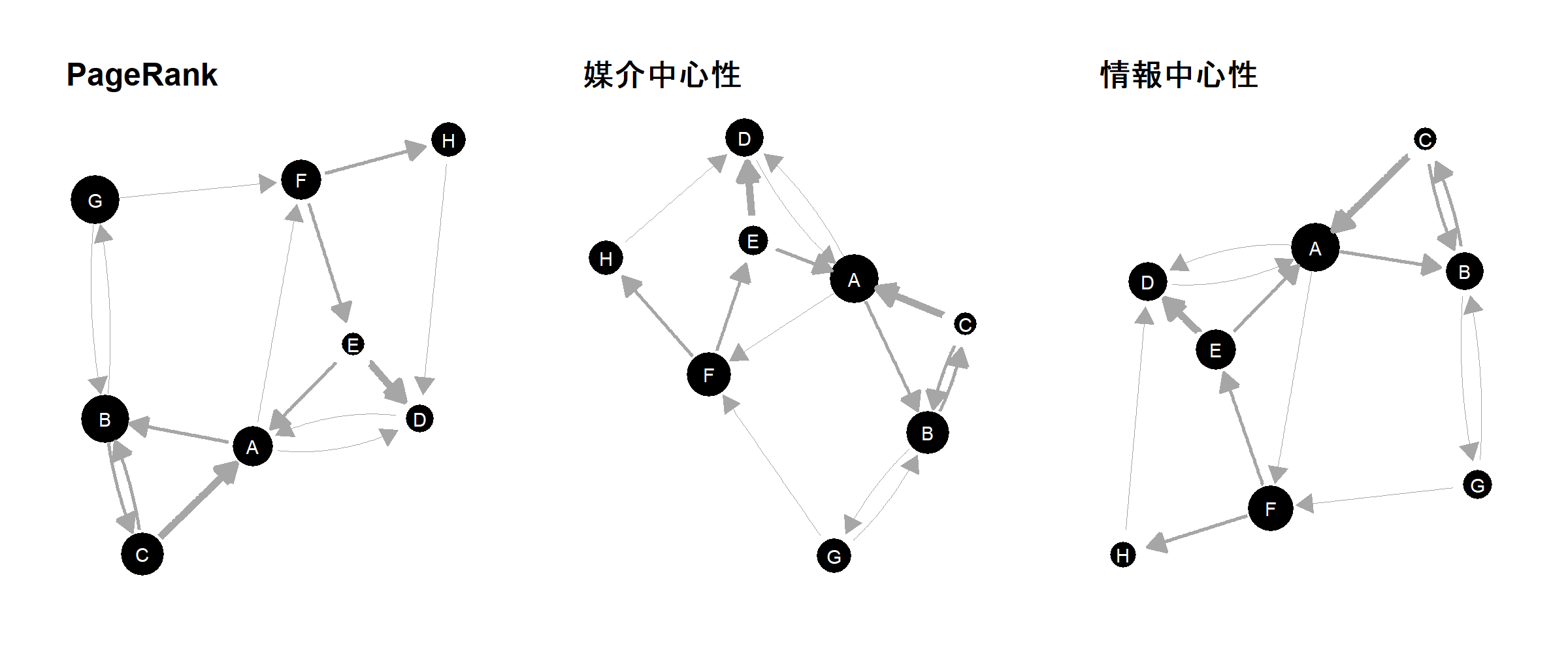
図3.9: PageRank・媒介中心性・情報中心性の値をノードの大きさに反映させたグラフ