1.2 社会ネットワークの基礎

1.2.1 グラフ

SNAでは、ネットワークの構造を頂点(ノード)と辺(エッジ)の集合によって表す。これを、グラフと呼ぶ。頂点は個体などを、辺は何らかの個体間の社会関係を表す。

関係の有無(1か0か)だけを考慮するグラフと、関係の強さ(交渉頻度など)も考慮するグラフがある。後者は特に重み付きグラフといい、関係の強さを「重み(weight)」という。グラフでは、エッジの太さで関係の強さを表す(図1.1)。
関係の向きを考える(\(A \rightarrow B\)と\(A \leftarrow B\)を区別)グラフを有向グラフ、考えないグラフを無向グラフという。有向グラフの場合は、辺に矢印を用いることが多い(図1.1のB)。

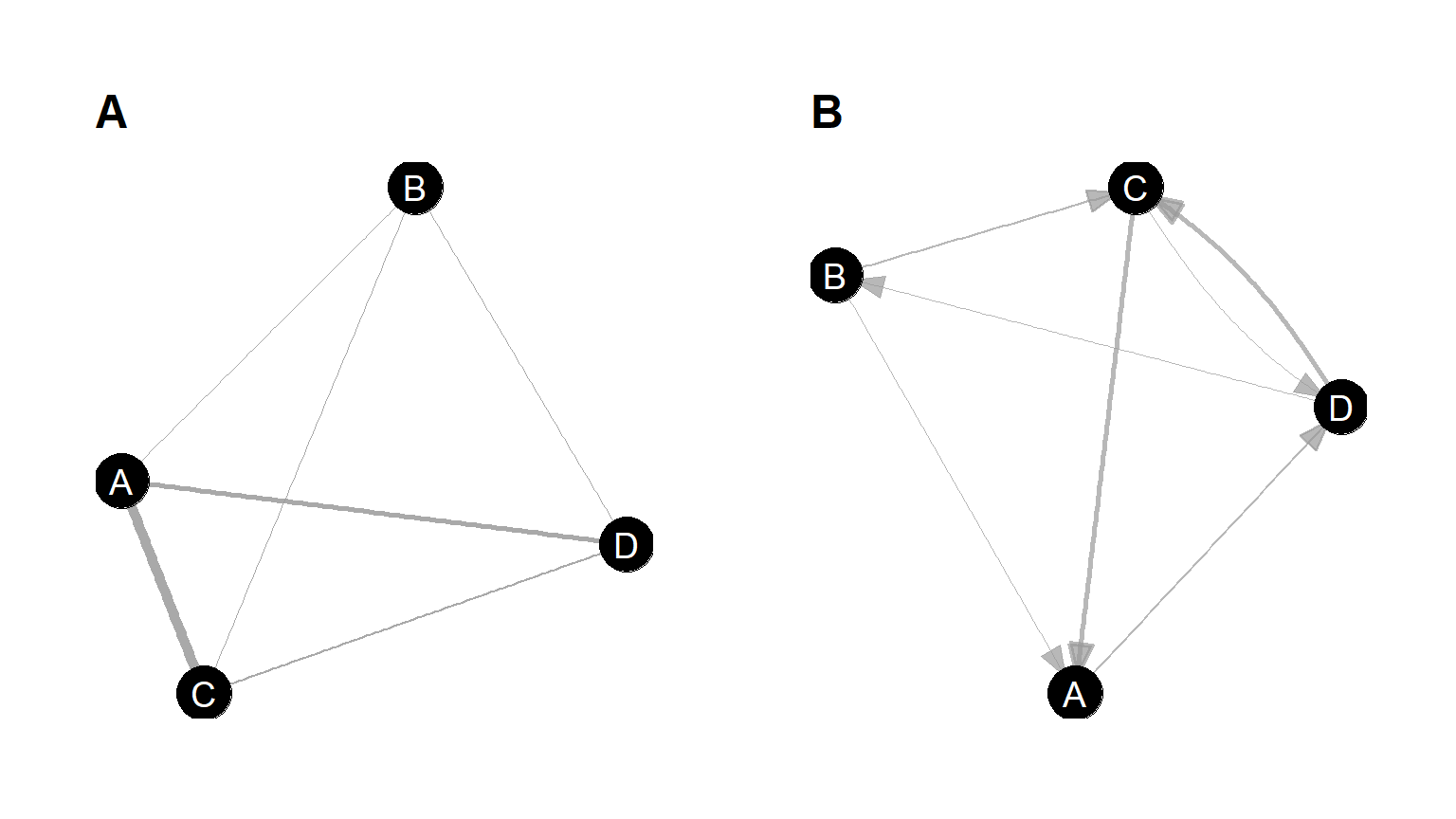
図1.1: 例1. 無向グラフ(A)と有向グラフ(B)の例

1.2.2 隣接行列(マトリックス)

ネットワーク分析では、データを隣接行列(adjacency matrix)の形で表現することが多い。隣接行列はグラフのノード間の関係が記された行列で、ノードの数が\(n\)個ならば、\(n \times n\)の正方行列になる。Rの分析でも、基本的に隣接行列を用いることが多い。

Rでは、matrix()関数によって以下のように作成できる。

mat_example <- matrix(## 数値のベクトル
                     c(0,0,0,2,
                       1.5,0,2,0,
                       3,0,0,1,
                       0,1,3,0),
                       ## 行数と列数
                       ncol = 4, nrow = 4,
                       ## TRUEなら、1行目から順に数値を入れていく
                       byrow = TRUE)

## 列名と行名を入れられる
colnames(mat_example) <- c("A","B","C","D")
rownames(mat_example) <- c("A","B","C","D")

## 完成したのがこちら
mat_example %>% 
  kable(digits = 2, align = "c",caption = "作成した隣接行列") %>% 
  kable_styling(font_size = 10, full_width = FALSE)

表1.1: 表1.2: 作成した隣接行列
	A	B	C	D
A	0.0	0	0	2
B	1.5	0	2	0
C	3.0	0	0	1
D	0.0	1	3	0

Excel等で作成したcsvファイルをデータフレームとして読み込み、それをマトリックスに変換する方法もある。

## 1列目を行名に指定
mat_example2 <- read.csv("data/example.csv", row.names = 1) 

## マトリックスに変換  
mat_example2 <- as.matrix(mat_example2)

mat_example2 %>% 
  kable(digits = 2, align = "c") %>% 
   kable_styling(font_size = 10, full_width = FALSE)

	A	B	C	D	E	F	G	H
A	0.00	0.55	0.15	0.93	0.86	0.29	0.63	0.24
B	0.41	0.00	0.86	0.95	0.20	0.99	0.36	0.59
C	0.09	0.41	0.00	0.87	0.63	0.85	0.29	0.80
D	0.83	0.68	0.07	0.00	0.60	0.54	0.14	0.42
E	0.80	0.82	0.34	0.68	0.00	0.70	0.41	0.43
F	0.80	0.05	0.78	0.17	0.95	0.00	0.04	0.37
G	0.75	0.42	0.90	0.95	0.51	0.16	0.00	0.05
H	0.87	0.16	0.02	0.05	0.31	0.85	0.13	0.00

1.2.3 Rでのグラフの描画

本稿ではggraphパッケージを用いる。このパッケージを用いる利点は主に以下の2点である。

tidygraphと併用することで、データフレーム形式のデータをそのままグラフにできる。それによって、データの加工とグラフの描画をシームレスに行いやすい。
ggplotパッケージの拡張なので、ggplotと同じ文法で描ける。

1.2.3.1 `tbl_graph`クラスへの変換

ggraphでグラフを描くには、データをtbl_graphクラスに変換する必要がある。隣接行列をas_tbl_graph()で変換してあげればよい。すると、ノードの名前nameと辺リスト(辺の始点、終点、重みが書いてあるリスト)が入ったオブジェクトを返してくれる。

## 有向グラフであれば directed = TRUE、無向グラフならFALSE
graph_mat_example2 <- as_tbl_graph(mat_example2, directed = TRUE)

graph_mat_example2

## # A tbl_graph: 8 nodes and 56 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 8 × 1 (active)
##   name 
##   <chr>
## 1 A    
## 2 B    
## 3 C    
## 4 D    
## 5 E    
## 6 F    
## 7 G    
## 8 H    
## #
## # Edge Data: 56 × 3
##    from    to weight
##   <int> <int>  <dbl>
## 1     1     2  0.552
## 2     1     3  0.153
## 3     1     4  0.930
## # ℹ 53 more rows

なお、各ノードの名前以外の情報もグラフに反映させたい場合は、以下のように情報を追加できる。ここでは、各個体の年齢の情報を追加した。

graph_mat_example2 %>% 
  mutate(age = c(12,10,15,6,20,13,8,7)) -> graph_mat_example2

graph_mat_example2

## # A tbl_graph: 8 nodes and 56 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 8 × 2 (active)
##   name    age
##   <chr> <dbl>
## 1 A        12
## 2 B        10
## 3 C        15
## 4 D         6
## 5 E        20
## 6 F        13
## 7 G         8
## 8 H         7
## #
## # Edge Data: 56 × 3
##    from    to weight
##   <int> <int>  <dbl>
## 1     1     2  0.552
## 2     1     3  0.153
## 3     1     4  0.930
## # ℹ 53 more rows

グラフに使用するデータを絞り込むなどの作業をする場合は、一度隣接行列を辺リストのデータフレームに変換してから(mat.to.edgl()で可能)データフレームを加工し、その後にas_tbl_graph()を用いるとよい。以下では、重みが0.7以上の辺のみを抽出している。

mat_example2 %>%
  ## 辺リストのデータフレームに変換
  mat.to.edgl() %>% 
  ## weightが0.5以上のものに限定する
　filter(weight >= 0.5) %>% 
  ## tbl_graphクラスに変換
  as_tbl_graph(directed = TRUE) %>% 
  mutate(age = c(12,10,15,6,20,13,8,7)) -> graph_mat_example2_b

graph_mat_example2

## # A tbl_graph: 8 nodes and 56 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 8 × 2 (active)
##   name    age
##   <chr> <dbl>
## 1 A        12
## 2 B        10
## 3 C        15
## 4 D         6
## 5 E        20
## 6 F        13
## 7 G         8
## 8 H         7
## #
## # Edge Data: 56 × 3
##    from    to weight
##   <int> <int>  <dbl>
## 1     1     2  0.552
## 2     1     3  0.153
## 3     1     4  0.930
## # ℹ 53 more rows

1.2.3.2 `ggraph`を用いた描画

ggraphでグラフを描画するときには、主に以下の3つを指定してあげればよい。

レイアウト: グラフでノードと辺をどのような規則に基づいて配置するかを決める。
例. line: 一直線、circle: 円上、nicely: いい感じに?、randomly: ランダムに、…
詳細はこちらやこちらを参照。
ノード: geom_node_*()(*には色々入る)という関数群でノードについて指定。関数の中でsize =で大きさ、color =で色、shape =で形などをggplotと同じように指定できる。
例. geom_node_point(): 普通のノード、geom_node_text(): ノードのラベル、…
辺(エッジ): geom_edge_*()(*には色々入る)という関数群でノードについて指定。関数の中でwidth =で太さ、color =で色などをggplotと同じように指定できる。
例: geom_edge_link(): 直線、geom_edge_fan(): 曲線、…

図1.2は実際に以下のコードで描いた例である。
layout = "nicely"とすると、グラフが見やすいように配置してくれる。関係のある(= 辺がある)個体同士はより近くに配置される傾向があるため、絶対とはいえないが、結果的に多くの個体と繋がっている個体が中心部に来る傾向がある。

何らかの指標を出さない限りグラフのみから何かを結論付けることはできないが、パッと見て関係構造の全体図を掴んだり、仮説を立てたりしようとする際にはグラフを見ることが非常に有用である。

graph_mat_example2_b %>% 
  # layoutの指定
  ggraph(layout = "nicely")+
  # 曲線のエッジ、weightを太さに
  geom_edge_fan(aes(width = weight),
                ## 矢印について指定
                 arrow = arrow(angle = 15, type = "closed",length = unit(0.18, "inches")),
                ## 矢印の終点のノードからの距離
                end_cap = circle(2.5,"mm"),
                ## 矢印の始点のノードからの距離
                start_cap = circle(2.5,"mm"),
                ## 透明度(alpha)と色(color)指定
                 alpha =0.7, color = "grey60")+
  # エッジの太さの範囲を決める  
  scale_edge_width(range = c(0,1.3))+
  ## 四角のノード。大きさは年齢によって変化するとする。  
  geom_node_point(aes(size = age), shape = 18)+
  ## ノードのラベルは個体名  
  scale_size(range = c(3,6))+
  geom_node_text(aes(label = name), 
                 ## ノードと重ならないようにする 
                 repel=TRUE, size =6)+
  theme_graph()+
  ## 縦横比
  theme(aspect.ratio = 0.7)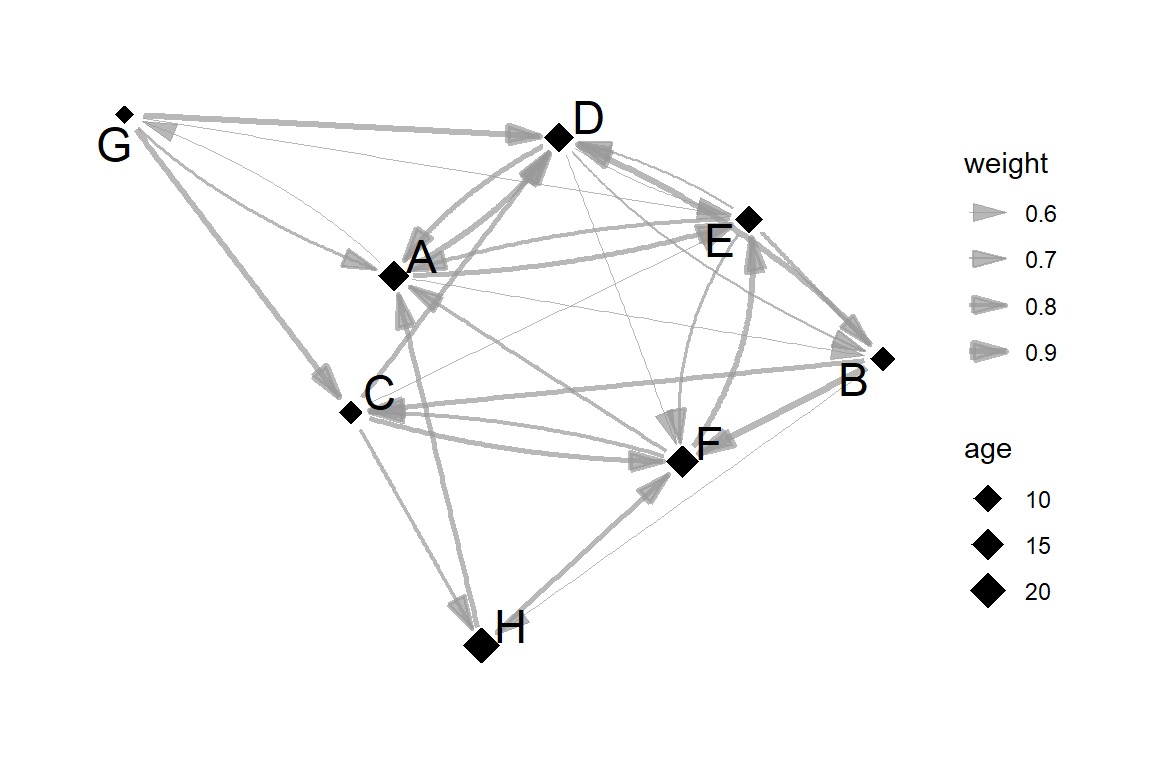

図1.2: ggraphで描いたグラフの例