補遺 ノンパラメトリックな推定
Allison (2014) ではほとんど解説がなかったが、分布に何も仮定を置かないノンパラメトリックな方法で分析を行うこともできる。以下では、2つの代表的な方法を紹介する。
Kaplan-Meier法
Kaplan-Maier法は生存関数を推定するための推定量で、時点\(t_n\)における生存率\(S_n\)の推定値は以下のように定義される。なお、時点\(t_n\)でのリスク集合の大きさを\(l_n\)、時点\(t_n\)に発生した事象の数を\(d_n\)としている。推定量は最尤推定によって得られる。
\[ \begin{aligned} S(t_n) &= \biggl(1-\frac{d_1}{l_1}\biggl) \times \biggl(1-\frac{d_2}{l_2}\biggl) \times \cdots \times \biggl(1-\frac{d_n}{l_n}\biggl) \\ &= \prod_{k=1}^n \biggl(1-\frac{d_k}{l_k}\biggl) \end{aligned} \]
Kaplan-Meier推定量は1からスタートし、事象の発生が確認されるたびに値が小さくなる階段関数である。Rではsurvivalパケージのsurvfit()関数で推定できる。ここでは、第2章で使用した生化学者の准教授への昇進データ(rank)を使用する。
第3章と第4章のモデルと同様に、従属変数をSurv(観察期間, 事象の発生の有無)もしくは、Surv(観察開始時点, 観察終了時点, 事象の発生の有無)として推定できる。推定の結果は以下のとおりである。
## Call: survfit(formula = Surv(dur, promo) ~ 1, data = rank, type = "kaplan-meier")
##
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 301 1 0.997 0.00332 0.990 1.000
## 2 299 1 0.993 0.00469 0.984 1.000
## 3 292 17 0.936 0.01431 0.908 0.964
## 4 263 42 0.786 0.02431 0.740 0.835
## 5 211 53 0.589 0.02970 0.533 0.650
## 6 149 46 0.407 0.03030 0.352 0.471
## 7 96 31 0.276 0.02825 0.225 0.337
## 8 59 15 0.205 0.02622 0.160 0.264
## 9 42 7 0.171 0.02484 0.129 0.228
## 10 29 4 0.148 0.02406 0.107 0.203結果の図示はsurvminerパッケージのggsurvplot()関数で行うことができる(図6.1)。
ggsurvplot(est_km,
data = rank,
censor = FALSE,
palette = "black",
size = 0.5,
conf.int.alpha = 0.15,
legend = "none",
legend.title = "") -> p_km
p_km$plot +
labs(x = "year")+
theme_bw(base_size = 16)+
theme(aspect.ratio = 1,
legend.position = "none")+
coord_cartesian(ylim = c(0.15,1))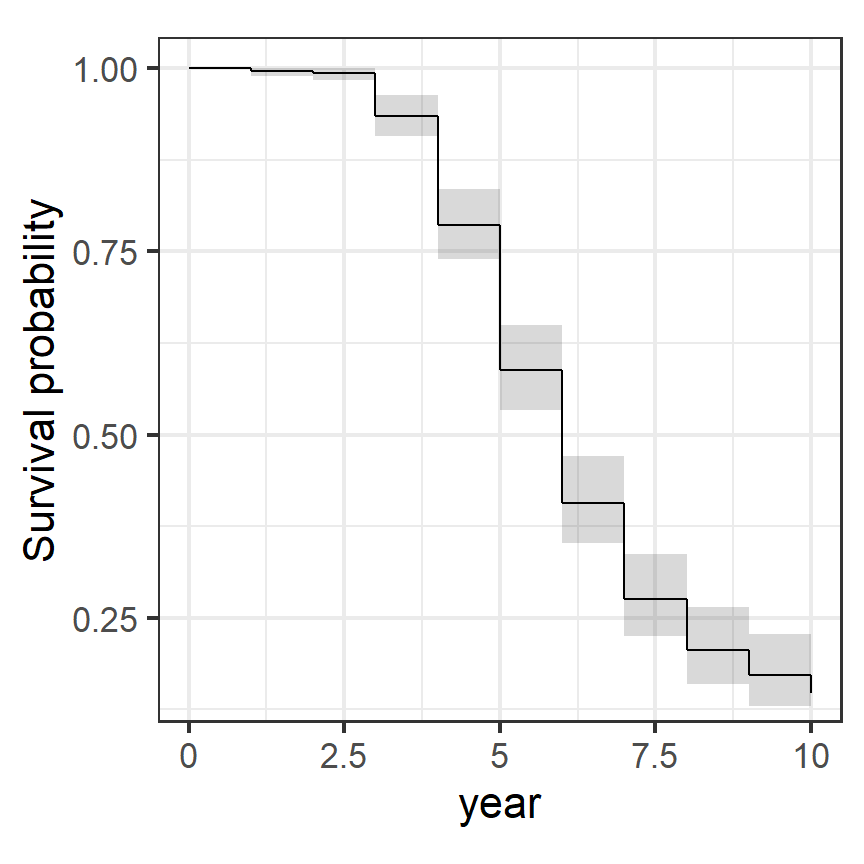
図6.1: Kaplan-Meier法で推定した生存曲線
説明変数を含めて、独立変数の値ごとに推定することもできる。
## Call: survfit(formula = Surv(dur, promo) ~ phdmed, data = rank, type = "kaplan-meier")
##
## phdmed=0
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 3 107 6 0.944 0.0222 0.9013 0.989
## 4 96 19 0.757 0.0423 0.6785 0.845
## 5 73 17 0.581 0.0496 0.4913 0.687
## 6 54 19 0.376 0.0496 0.2908 0.487
## 7 31 11 0.243 0.0455 0.1682 0.351
## 8 17 4 0.186 0.0428 0.1182 0.292
## 9 13 3 0.143 0.0395 0.0831 0.245
## 10 8 1 0.125 0.0383 0.0685 0.228
##
## phdmed=1
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 189 1 0.995 0.00528 0.984 1.000
## 2 188 1 0.989 0.00744 0.975 1.000
## 3 185 11 0.931 0.01857 0.895 0.968
## 4 167 23 0.802 0.02953 0.747 0.862
## 5 138 36 0.593 0.03710 0.525 0.670
## 6 95 27 0.425 0.03819 0.356 0.506
## 7 65 20 0.294 0.03591 0.231 0.373
## 8 42 11 0.217 0.03317 0.161 0.293
## 9 29 4 0.187 0.03179 0.134 0.261
## 10 21 3 0.160 0.03076 0.110 0.233また、2つ以上の集団で生存関数が有意に異なるかを、ログランク検定や一般化ウィルコクソン検定で調べることもできる。Rではsurvdiff()関数で以下のように実行することができる。今回は、医学博士を持っているか否か(phdmed)によって生存関数が有意に異なるわけではないことが分かった。コックス回帰などとは異なり、他の変数の影響を統制できない点は注意が必要である。
## Call:
## survdiff(formula = Surv(dur, promo) ~ phdmed, data = rank, rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## phdmed=0 112 80 74.9 0.345 0.685
## phdmed=1 189 137 142.1 0.182 0.685
##
## Chisq= 0.7 on 1 degrees of freedom, p= 0.4## Call:
## survdiff(formula = Surv(dur, promo) ~ phdmed, data = rank, rho = 1)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## phdmed=0 112 54.6 51.4 0.206 0.516
## phdmed=1 189 91.1 94.4 0.112 0.516
##
## Chisq= 0.5 on 1 degrees of freedom, p= 0.5検定の結果を反映させた図を作成することもできる(図6.2)。
ggsurvplot(est_km2,
data = rank,
censor = FALSE,
conf.int = TRUE,
palette = c("blue3","red2"),
size = 0.5,
conf.int.alpha = 0.15,
legend.title = "",
## p値を表示
pval = TRUE,
## 一般化ウィルコクソン検定の場合は"S1"
log.rank.weights = "1") -> p_km2
p_km2$plot +
labs(x = "year")+
theme_bw(base_size = 16)+
theme(aspect.ratio = 1,
legend.position = "top")+
coord_cartesian(ylim = c(0.15,1))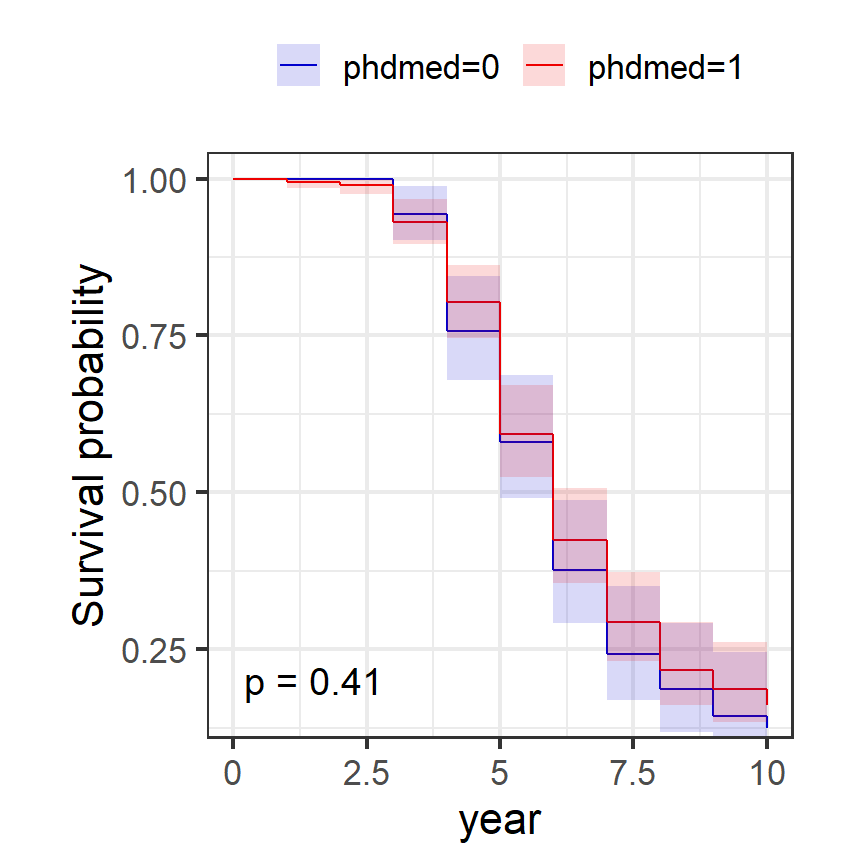
図6.2: ロングランク検定の結果を示した生存曲線
Nelson-Aalen法
もう一つよく用いられる方法がNelson-Aalen法であり、累積ハザード関数(ある時点までのハザード率の総和)を推定するための推定量である。時点\(t_n\)における累積ハザード率\(H_n\)の推定値は以下のように定義される。なお、時点\(t_n\)でのリスク集合の大きさを\(l_n\)、時点\(t_n\)に発生した事象の数を\(d_n\)としている。
\[ \begin{aligned} H(t_n) &= \biggl(\frac{d_1}{l_1}\biggl) + \biggl(\frac{d_2}{l_2}\biggl) + \cdots + \biggl(\frac{d_n}{l_n}\biggl) \\ &= \sum_{k=1}^n \biggl(\frac{d_k}{l_k}\biggl) \end{aligned} \]
Nelson-Aalen推定量は0からスタートし、事象の発生が確認されるたびに値が大きくなる階段関数である。Rではcoxph()で説明変数のないモデルを推定したのち、basehaz()関数で求められる。
結果の図示はsurvminerパッケージのggsurvplot()関数で、fun = "cumhaz"とすることで行うことができる(図6.3)。
fit_na <- survfit(est_na,
data = rank,
## 信頼区間の範囲
conf.int = 0.95)
ggsurvplot(fit_na,
fun = "cumhaz",
data = rank,
censor = FALSE,
legend = "none") -> p_na
p_na$plot +
labs(x = "year")+
theme_bw(base_size = 16)+
theme(aspect.ratio = 1,
legend.position = "none")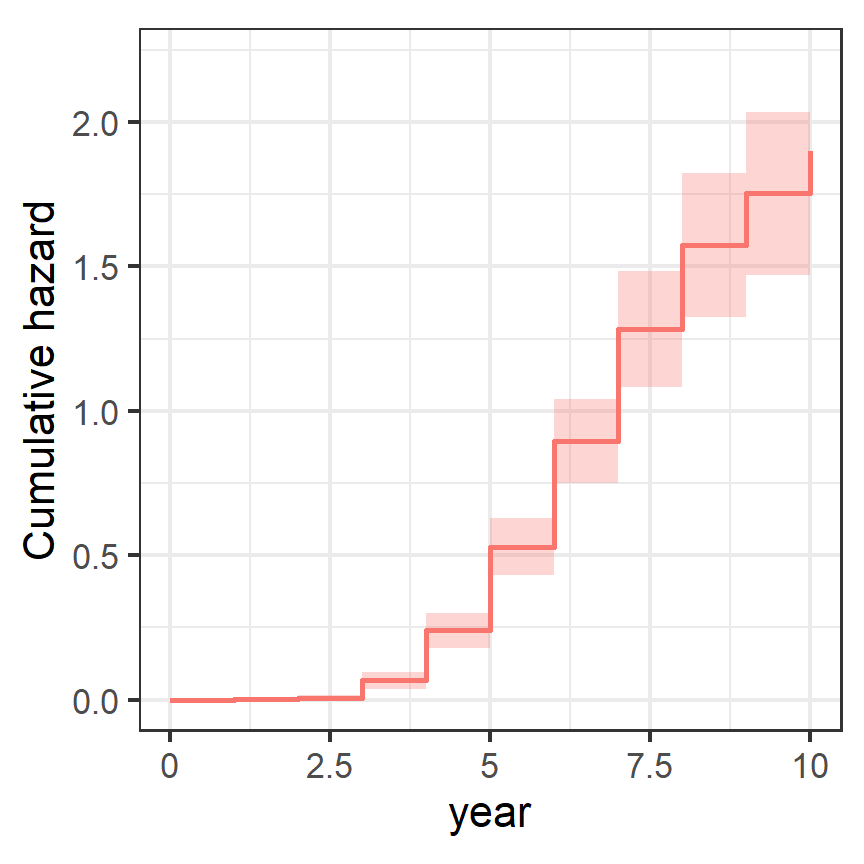
図6.3: Nelson-Aalen法で推定した累積ハザード関数
生存関数\(S_n\)と累積ハザード関数\(H(t_n)\)の関係は以下のように記述できる。よって、Nelson-Aalen法で推定した累積ハザード関数から生存関数を推定することもできる。
\[ S(t_n) = exp[-H(t_n)] \]
Nelson-Aalen法によって推定された生存関数は以下のように図示できる。
est_na2 <- survfit(Surv(dur, promo) ~ 1,
data = rank,
type = "fh")
ggsurvplot(est_na2,
data = rank,
censor = FALSE,
legend = "none",
palette = "black",
conf.int.alpha = 0.15,
size = 0.5) -> p_na2
p_na2$plot +
labs(x = "year")+
theme_bw(base_size = 16)+
theme(aspect.ratio = 1,
legend.position = "none")+
coord_cartesian(ylim = c(0.15,1))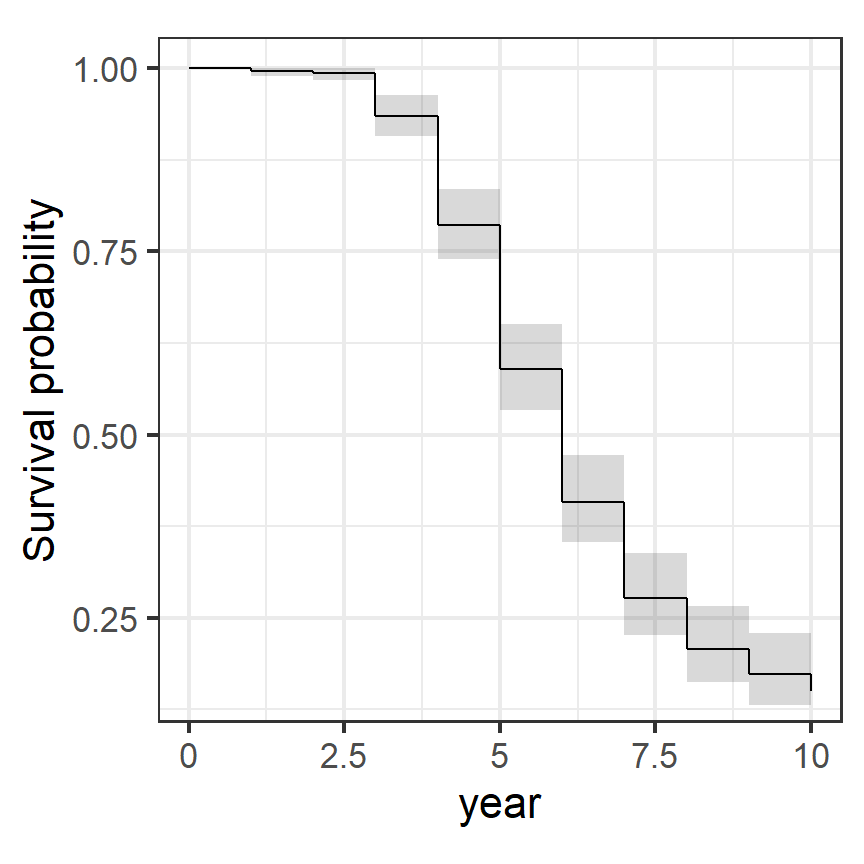
図6.4: Nelson-Aalen法で推定した生存曲線