5 複数事象のモデル
これまでの章では、分析対象の事象を全て同じように扱ってきた。例えば、第2章では昇進の種類を区別していないし、第3~4章は再犯の際の犯罪の種類を区別していない。本章では、複数の事象がある場合に分析を行う方法を解説する。基本的には、一種類の事象の場合に解説した方法を応用できる。
5.1 複数事象の分類
まず話を簡単にするために、二種類の事象がある場合のみに限定して事象が発生する状況を分類する。なお、繰り返しのある事象については次章(6)で解説する。
5.1.1 条件付き過程
まず一つ目は条件付き過程であり、次のように定義される。
- 事象の発生または非発生は一連の因果プロセスによって決定される。ある条件が与えられた後、因果メカニズムによってどの種類の事象が発生するかが決定される。
例としては、携帯電話を購入することを決定した後、iPhoneとAndroidのどちらを購入するかを決定する場合などが挙げられる。こうしたタイプに対して適切な分析は、⓵まずイベント・ヒストリー分析を行って事象の区別をせずに事象の発生だけに着目した分析を行い、⓶どの種類の事象が発生するかを別のモデル(通常は二項ロジットモデルや多項ロジットモデル)で分析する。
5.1.2 並行的過程
5.1.2.1 4つのタイプ
次に考えられるのは並行的過程と呼ばれるタイプのものであり、次の条件を満たす。
- それぞれの種類の事象の発生は異なる因果メカニズムによって決定される。
異なる因果メカニズムとは、それぞれの種類の事象の発生が異なる独立変数によって影響されたり、同じ独立変数が事象の種類によって異なる偏回帰係数や線形関数を持っていたりすることを指す。この仮定は、以下の4つの下位タイプに分類できる。
2a. ある種類の事象を経験した個体はほかの種類の事象を経験する可能性がなくなる(= 競合リスク)。
例としては、競合する原因による死亡などが挙げられる。心臓病とがんの両方が原因で死亡する可能性はないので、心臓病が原因で死亡した個体はもはやがんで死亡する可能性がない。2b. ある種類の事象を経験すると、その個体はほかの種類の事象の観察対象から外れる。
例えば国内移動と国外移動を考えるとき、もし個体が国外移動するとその個体を追跡することが困難になることが珍しくない。2c. ある一つの種類の事象を経験しても、他の種類の事象を経験する可能性や個体の観察の継続性に影響を与えない。
二つの種類の事象が全く無関係であることはないが、分析する際にあたかも無関係のように扱うことが可能な場合はある。例えば、選挙で投票に行くことと結婚することはほとんど関係がないと仮定できるので、そのように扱える。2d. ある一つの事象が生じると、ほかの種類の事象を経験する可能性が増大/減少する。
例えば、妊娠すると結婚する可能性が高まる、といった場合がこれに該当する
5.1.2.2 並行的過程のタイプごとの分析
2c
それぞれの種類の事象が独立すると仮定できるので、前章までの分析をそれぞれに適用すればよい。2d
二つ目の事象について検討する際に必ず一つ目についても考慮する必要がある。この方法はすでに前章までに解説しており、要するに一つ目の事象を時間依存的な独立変数として扱ってしまえばよい。例えば元服役囚の再犯の例では、各週ごとに就業しているかを独立変数に加えていた。2b
ある種類の事象の発生によって、他の種類の発生についての右側打ち切りが生じている例である。このタイプは、前章までの方法で分析することができる。すなわち、ある事象を経験することで個体が観察から脱落してしまったら、その時点で打ち切りが生じたかのように扱えばよい。2a
このタイプに対する分析は2bと似ているが、さらに詳しい解説が必要である。次章以降では、こうしたタイプの事象を扱う「競合リスク・モデル」について解説する。
5.2 競合リスク・モデル
5.2.1 モデルの概要
競合リスクのある事象を分析する方法で最も一般的なものは、タイプ固有(type-specific)ハザード関数と呼ばれるものを定義する方法である。\(m\)種類の異なる事象があり、\(j = 1,2,...,m\)とする。\(P_j(t,t+s)\)を陸巣集合に入っている個体が種類\(j\)の事象を時点\(t\)から\(t+s\)の期間で経験する条件付き確率とする。ただし、個体が時点\(t\)より前に\(m\)個の事象のいずれかを経験していたらリスク集合には入っていないものとする。
タイプ固有ハザード関数は以下のように定義される。各種類の事象に独自のハザード関数が定義される。
\[
h_j(t) \lim_{s \rightarrow 0} \frac{P_j(t,t+s)}{s}
\]
分析では、タイプ固有のハザード関数一つひとつについてモデルを作ることができる。前章までに説明したイベント・ヒストリーのモデルはどれも競合リスクの分析に用いることができる。次章の種類によって全く異なるモデルを当てはめることも可能である。いずれのモデルでも事象の種類ごとに別々に尤度関数を作り、最尤推定法または部分尤度推定法でパラメータを推定する。
5.2.2 Rでの実装
分析の例として、元服役囚の再犯についての研究を再度取り上げる。再犯で逮捕された犯罪を財産犯(強盗・窃盗など)とそれ以外に分ける。経済的支援は財産犯による再犯のリスクは減らす可能性があるが、それ以外の犯罪には大きく影響するとは考えられない。
ここでは、以下の式のコックス比例ハザードモデルで推定を行う(式(5.1))。いずれの種類の事象にも同じ独立変数を考えるが、偏回帰係数は異なるとしている。
\[ log(h_j(t)) = a_j(t) + b_{j1}x_1 + b_{j2}x_2 + \cdots \tag{5.1} \]
変数は以下の通り。今回は時間依存変数は含めない。
従属変数に関わるもの
- arrest: 再犯の有無
- type: 再犯の種類(0: 再犯なし、1: 非財産犯、2: 財産犯)
- arrstday: 再逮捕されたときに出所後何日だったか
独立変数
- fin: 経済的支援の有無
- white: 人種(白人か否か)
- edcomb: 教育レベル(学校教育を受けた年数)
- married: 出所時の配偶状態(0/1)
- age: 出所時の年齢
- male: 性別(0/1)
- numarst: 前科の数
- numprop: 過去の財産犯の有罪判決の数
- crimprop: 最後の服役が財産犯によるものか(0/1)
- paro: 出所が仮釈放か否か(0/1)
データは以下のとおりである。
データを見ると、打ち切りになった個体(type = 0)が598人、非財産犯で逮捕された個体(type = 1)が137人、財産犯で逮捕された個体(type = 2)が197人いたことが分かる(表5.1)。
tarp %>%
group_by(type) %>%
summarise(N = n()) %>%
kable(caption = "財産犯/非財産犯で逮捕された個体数") %>%
kable_styling(font_size = 15, full_width = FALSE)| type | N |
|---|---|
| 0 | 598 |
| 1 | 137 |
| 2 | 197 |
5.2.2.1 事象の種類を区別しないで分析
まず、再犯による逮捕の種類を区別しないモデルを以下のように推定する。これは前章で解説した方法と全く一緒である。
mod_rsk_all <- coxph(Surv(arrstday,arrest) ~ fin + age + white + male + married + paro + numprop +
crimprop + numarst + edcomb, data = tarp)結果は以下の通り。age、white、numprop、crimprop、numarrst、edcombの影響が5%水準で有意になっている。
## Call:
## coxph(formula = Surv(arrstday, arrest) ~ fin + age + white +
## male + married + paro + numprop + crimprop + numarst + edcomb,
## data = tarp)
##
## coef exp(coef) se(coef) z p
## fin 0.120982 1.128605 0.113735 1.064 0.287456
## age -0.034417 0.966168 0.008578 -4.012 6.01e-05
## white -0.240927 0.785899 0.118271 -2.037 0.041643
## male 0.501650 1.651443 0.309194 1.622 0.104708
## married -0.221696 0.801159 0.129709 -1.709 0.087418
## paro -0.211252 0.809570 0.118415 -1.784 0.074425
## numprop 0.310299 1.363832 0.071903 4.316 1.59e-05
## crimprop 0.424965 1.529536 0.137179 3.098 0.001949
## numarst 0.017689 1.017847 0.004638 3.814 0.000137
## edcomb -0.067607 0.934628 0.025304 -2.672 0.007544
##
## Likelihood ratio test=85.33 on 10 df, p=4.497e-14
## n= 932, number of events= 334ggforest()関数によって図示した結果が図5.1である。
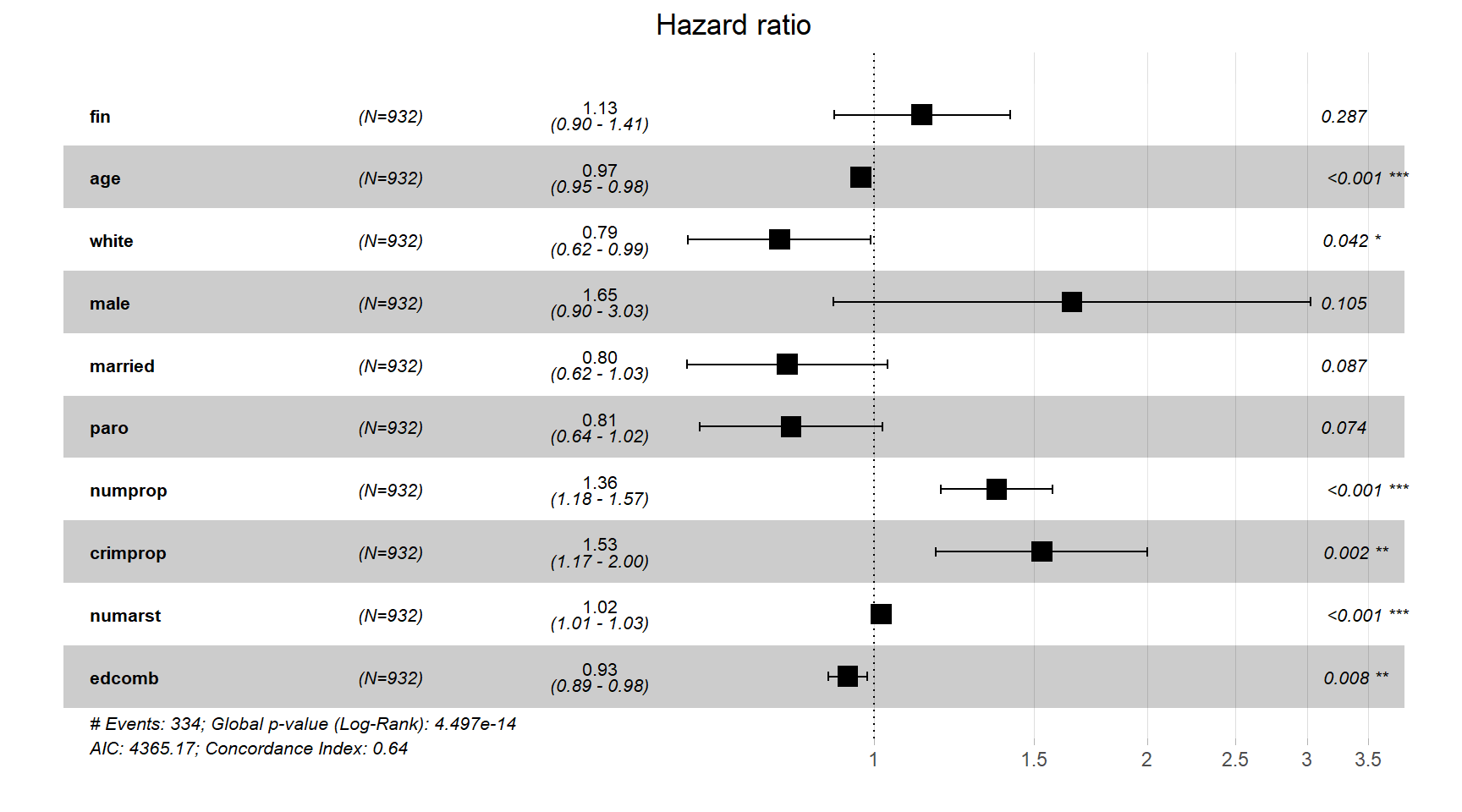
図5.1: mod_rsk_allで推定されたハザード比
5.2.2.2 再犯の種類ごとに分析
それぞれの独立変数は再犯の種類ごとに異なる影響を与えている可能性があるため、財産犯とそうでない再犯に分けて比例ハザードモデルを推定する。財産犯について分析する際は、非財産犯で逮捕された個体は打ち切りとして扱い、非財産犯について分析する際はその逆である。
データフレームに財産犯で再犯を犯した場合は1、それ以外は0とする列を作成する(prop)。非財産犯についても同様の列を作成する(non_prop)。
tarp %>%
mutate(prop = ifelse(type == "2", 1, 0)) %>%
mutate(non_prop = ifelse(type == "1", 1, 0)) -> tarp5.2.2.2.1 財産犯についての分析
財産犯についてモデリングした結果は以下のとおりである。
mod_rsk_prop <- coxph(Surv(arrstday,prop) ~ fin + age + white + male + married + paro + numprop +
crimprop + numarst + edcomb, data = tarp)
mod_rsk_prop## Call:
## coxph(formula = Surv(arrstday, prop) ~ fin + age + white + male +
## married + paro + numprop + crimprop + numarst + edcomb, data = tarp)
##
## coef exp(coef) se(coef) z p
## fin 0.201143 1.222800 0.149431 1.346 0.178284
## age -0.041430 0.959416 0.012239 -3.385 0.000712
## white -0.353086 0.702517 0.155856 -2.265 0.023484
## male 0.111079 1.117483 0.345574 0.321 0.747881
## married -0.332356 0.717232 0.177081 -1.877 0.060537
## paro -0.146924 0.863360 0.153704 -0.956 0.339129
## numprop 0.318580 1.375173 0.097219 3.277 0.001049
## crimprop 0.883210 2.418651 0.205986 4.288 1.81e-05
## numarst 0.018666 1.018841 0.006264 2.980 0.002886
## edcomb -0.053404 0.947997 0.034110 -1.566 0.117428
##
## Likelihood ratio test=79.48 on 10 df, p=6.359e-13
## n= 932, number of events= 197ggforest()関数によって図示した結果が図5.2である。事象を区別しなかった場合と異なり、教育レベル(edcomb)が5%水準で有意にならなかったが、それ以外は同じ独立変数が有意になり、効果の方向性も変わらなかった。
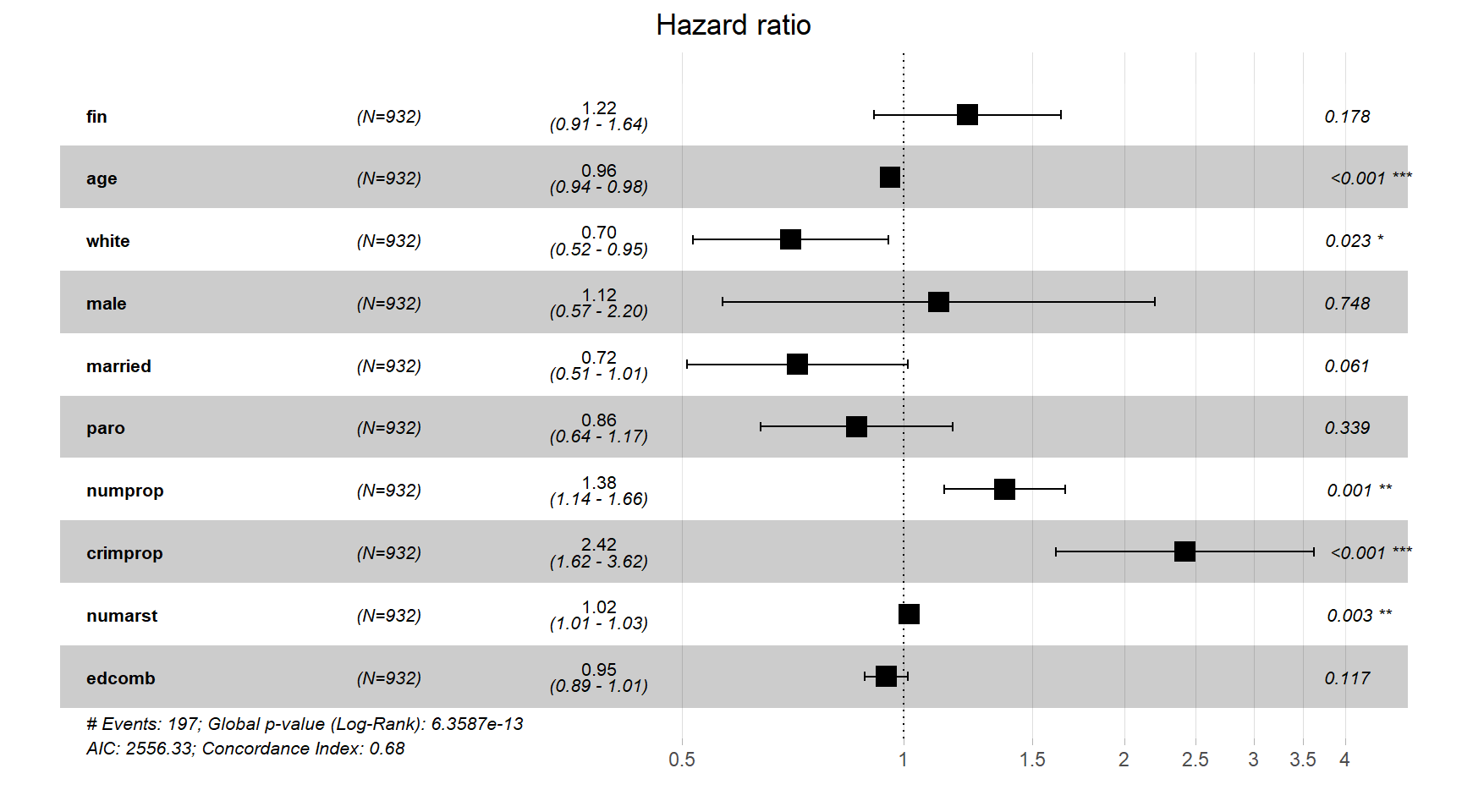
図5.2: mod_rsk_propで推定されたハザード比
5.2.2.2.2 非財産犯についての分析
財産犯についてモデリングした結果は以下のとおりである。
mod_rsk_nonprop <- coxph(Surv(arrstday,non_prop) ~ fin + age + white + male + married + paro + numprop +
crimprop + numarst + edcomb, data = tarp)
mod_rsk_nonprop## Call:
## coxph(formula = Surv(arrstday, non_prop) ~ fin + age + white +
## male + married + paro + numprop + crimprop + numarst + edcomb,
## data = tarp)
##
## coef exp(coef) se(coef) z p
## fin 0.007344 1.007371 0.175793 0.042 0.9667
## age -0.027191 0.973175 0.012037 -2.259 0.0239
## white -0.077279 0.925632 0.182082 -0.424 0.6713
## male 1.387656 4.005452 0.714747 1.941 0.0522
## married -0.073327 0.929297 0.192562 -0.381 0.7034
## paro -0.302124 0.739246 0.186428 -1.621 0.1051
## numprop 0.308181 1.360947 0.107084 2.878 0.0040
## crimprop -0.068915 0.933406 0.192115 -0.359 0.7198
## numarst 0.016305 1.016438 0.006936 2.351 0.0187
## edcomb -0.082639 0.920684 0.037831 -2.184 0.0289
##
## Likelihood ratio test=29.47 on 10 df, p=0.001044
## n= 932, number of events= 137ggforest()関数によって図示した結果が図5.3である。age、numprop、numarrst、edcombの4つのみが5%水準で有意に影響しているという結果になった。
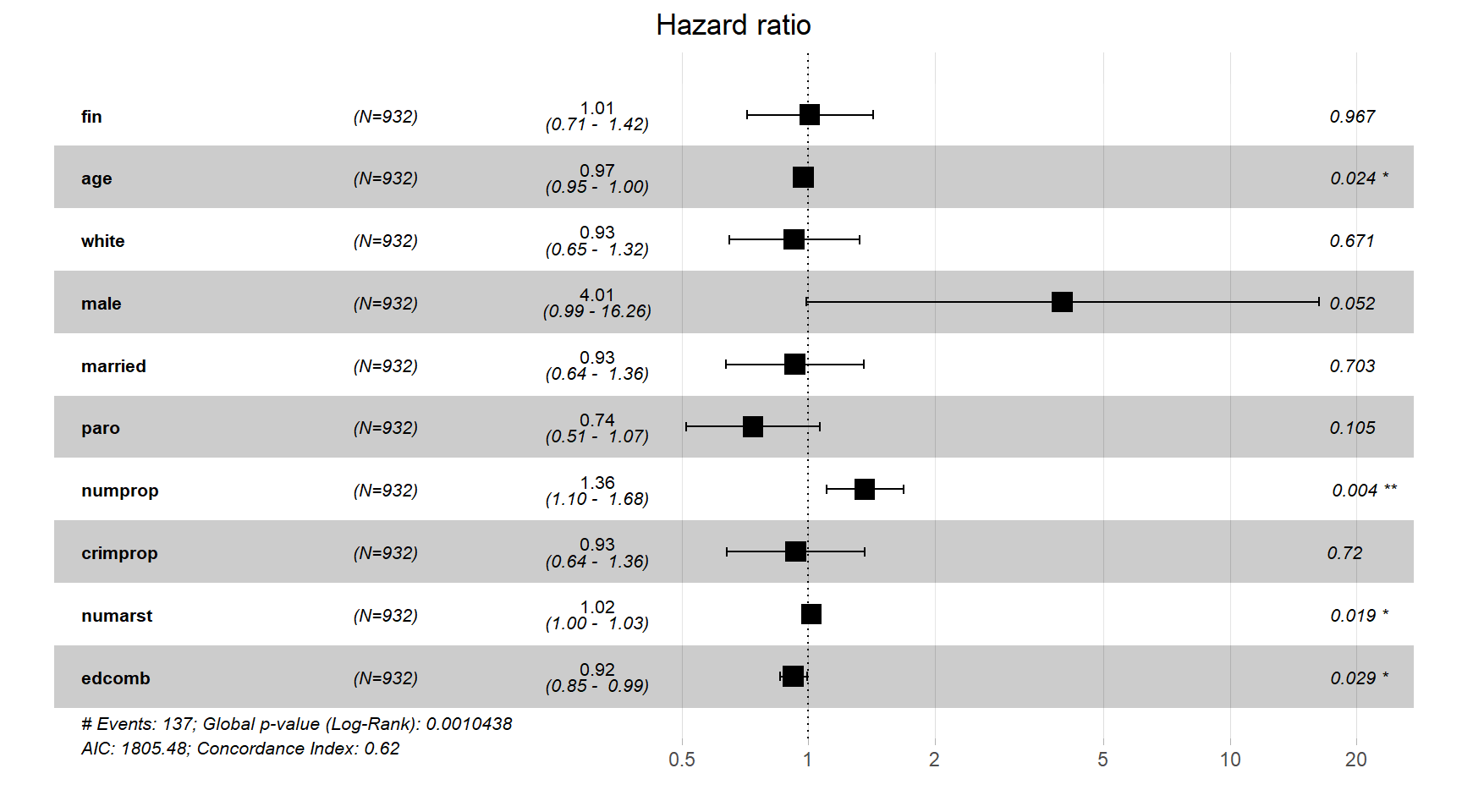
図5.3: mod_rsk_nonpropで推定されたハザード比
5.2.2.2.3 結果の比較
以上の3つのモデルで推定された偏回帰係数を比較したのが表5.2である。経済的支援(fin)はいずれでも有意ではなかったが、財産犯で最も大きな影響を持っていた。しかし、偏回帰係数の符号は予想とは逆であり、経済的支援をした元服役囚の方が、していない服役囚よりも財産犯を犯すリスクが高い傾向にあった。年齢(age)、過去に犯した財産犯の有罪判決の数(numprop)、前科の数(numarrst)はいずれのモデルでも再犯に影響を与えていたが、人種(white)は非財産犯のみで有意な影響がみられなかった。また、最後の服役が財産犯であったか(cromprop)も非財産犯のみで有意でなかったが、教育レベル(edcomb)は逆に財産犯のみで有意でなかった。
tibble(Covariate = rownames(mod_rsk_all$coefficients %>% data.frame()),
"Coef(all)" = c(sprintf("%.3f",coef(mod_rsk_all))[1:10]),
"Exp(Coef_all)" = c(sprintf("%.3f",exp(coef(mod_rsk_all)))[1:10]),
"Coef(prop)" = sprintf("%.3f",coef(mod_rsk_prop))[1:10],
"Exp(Coef_prop)" = sprintf("%.3f",exp(coef(mod_rsk_prop)))[1:10],
"Coef(nonprop)" = sprintf("%.3f",coef(mod_rsk_nonprop))[1:10],
"Exp(Coef_nonprop)" = sprintf("%.3f",exp(coef(mod_rsk_nonprop))[1:10])) %>%
flextable() %>%
add_header_row(colwidth = c(1,2,2,2),
values = c("","全ての種類","財産犯", "非財産犯")) %>%
flextable::align(align = "center", part = "all") %>%
set_caption("各モデルの推定値の比較")全ての種類 | 財産犯 | 非財産犯 | ||||
|---|---|---|---|---|---|---|
Covariate | Coef(all) | Exp(Coef_all) | Coef(prop) | Exp(Coef_prop) | Coef(nonprop) | Exp(Coef_nonprop) |
fin | 0.121 | 1.129 | 0.201 | 1.223 | 0.007 | 1.007 |
age | -0.034 | 0.966 | -0.041 | 0.959 | -0.027 | 0.973 |
white | -0.241 | 0.786 | -0.353 | 0.703 | -0.077 | 0.926 |
male | 0.502 | 1.651 | 0.111 | 1.117 | 1.388 | 4.005 |
married | -0.222 | 0.801 | -0.332 | 0.717 | -0.073 | 0.929 |
paro | -0.211 | 0.810 | -0.147 | 0.863 | -0.302 | 0.739 |
numprop | 0.310 | 1.364 | 0.319 | 1.375 | 0.308 | 1.361 |
crimprop | 0.425 | 1.530 | 0.883 | 2.419 | -0.069 | 0.933 |
numarst | 0.018 | 1.018 | 0.019 | 1.019 | 0.016 | 1.016 |
edcomb | -0.068 | 0.935 | -0.053 | 0.948 | -0.083 | 0.921 |
では、財産犯についてのモデル(mod_rsk_prop)と非財産犯についてのモデル(mod_rsk_nonprop)で推定された偏回帰係数の差は統計的に有意だろうか。以下の統計量\(z\)は二つの偏回帰係数に差がないという帰無仮説の下では理論上標準正規分布に従う。つまり、\(z < -1.96\)または\(z > 1.96\)であれば、二つの偏回帰係数は有意に異なるということになる。なお、\(se(b_1)\)と\(se(b_2)\)はそれぞれ偏回帰係数\(b_1\)と\(b_2\)の標準誤差である。
\[ z = \frac{b_1 - b_2}{\sqrt se(b_1)^2 + se(b_2)^2 } \]
各独立変数について\(z\)を計算したのが表5.3である。最後の服役が財産犯であったか(cromprop)のみが5%水準で有意に偏回帰係数の推定値が異なっていた。
tibble(
Covariate = rownames(mod_rsk_all$coefficients %>% data.frame()),
b_prop = mod_rsk_prop$coefficients,
se_b_prop = sqrt(diag(mod_rsk_prop$var)),
b_nonprop = mod_rsk_nonprop$coefficients,
se_b_nonprop = sqrt(diag(mod_rsk_nonprop$var))) %>%
mutate(z = (b_prop - b_nonprop)/sqrt(se_b_prop^2 + se_b_nonprop^2)) %>%
mutate_if(.predicate = is.numeric, .funs = ~sprintf("%.3f",.)) %>%
kable(caption = "各独立変数についてのz値") %>%
kable_styling(font_size = 11, full_width = FALSE)| Covariate | b_prop | se_b_prop | b_nonprop | se_b_nonprop | z |
|---|---|---|---|---|---|
| fin | 0.201 | 0.149 | 0.007 | 0.176 | 0.840 |
| age | -0.041 | 0.012 | -0.027 | 0.012 | -0.829 |
| white | -0.353 | 0.156 | -0.077 | 0.182 | -1.151 |
| male | 0.111 | 0.346 | 1.388 | 0.715 | -1.608 |
| married | -0.332 | 0.177 | -0.073 | 0.193 | -0.990 |
| paro | -0.147 | 0.154 | -0.302 | 0.186 | 0.642 |
| numprop | 0.319 | 0.097 | 0.308 | 0.107 | 0.072 |
| crimprop | 0.883 | 0.206 | -0.069 | 0.192 | 3.380 |
| numarst | 0.019 | 0.006 | 0.016 | 0.007 | 0.253 |
| edcomb | -0.053 | 0.034 | -0.083 | 0.038 | 0.574 |
5.2.3 注意点
競合リスク・モデルでは、他の種類の事象が発生したことにより生じた打ち切りについてはモデル中に情報がないので、ランダムな打ち切りでなくてはならない(2.8参照)。こうした無情報性の仮定が妥当かは検定することができない。ただし、すべての種類の事象の発生に影響を与える独立変数がモデルに十分に含まれているのであれば、打ち切りが無情報になる可能性は高くなるので、その点に留意してモデリングすることはできる。
5.3 部分分布を用いた競合リスクの分析
5.3.1 モデルの概要
競合事象を分析するもう一つの方法は、部分分布を用いる方法である。この方法は打ち切りが無情報である必要がない。一方で、分析目的が予測のときには有益だが、因果関係の推論には適していないとされる。
ここで、\(j = 1,2,3,...,k\)個の競合する事象があったとする。時点\(t\)において事象\(j\)が発生する確率を\(f_j(t)\)とすると、時点\(t\)までの事象\(j\)の累積発生率関数(= 時点\(t\)までに事象\(j\)が発生する確率)は以下のように定義され、部分分布(subdistribution)あるいは累積発生率関数(cumulative incidence function)と呼ばれる。
\[ F_j(t) = \int_0^t f_j(u) du \]
一方で、時点\(t\)までの全ての事象の累積発生率関数は
\[ F(t) = \sum_{j=1}^k F_j(t) \]
で表され、生存関数は\(S(t) = 1-F(t)\)と書くことができる。このとき、事象\(j\)のハザード関数は以下のようになる。
\[ h_j(t) = f_j(t)/S(t) \]
独立変数を\(x\)、偏回帰係数を\(\beta\)とすると、部分分布のハザード関数に基づいた競合リスクの比例ハザードモデルは以下のように書ける。
\[
h_j(t,x_i) = h_j(t) \times exp(\beta x_i)
\]
5.3.2 Rでの実装
Rでは、tidycmprskパッケージのcrr()関数を用いて部分分布を使った分析を行える。
## 事象の種類を表す変数は因子型でなくてはならない。
tarp <- mutate(tarp, type2 = as.factor(type))
## 財産犯のモデル
mod_subd_prop <- tidycmprsk::crr(Surv(arrstday,type2) ~ fin + age + white + male + married + paro + numprop +
crimprop + numarst + edcomb,
## 着目する事象の種類。ここでは財産犯。
failcode = 2,
data = tarp)
## 非財産犯のモデル
mod_subd_nonprop <- tidycmprsk::crr(Surv(arrstday,type2) ~ fin + age + white + male + married + paro + numprop +
crimprop + numarst + edcomb,
## 着目する事象の種類。ここでは非財産犯。
failcode = 1,
data = tarp)財産犯に着目したモデルの結果は以下の通り。HRはハザード比(偏回帰係数を対数変換したもの)を表す。age、white、married、numprop、crimprop、numarrstの影響が5%水準で有意になっていた。
##
## Variable Coef SE HR 95% CI p-value
## fin 0.236 0.152 1.27 0.94, 1.70 0.12
## age -0.040 0.014 0.96 0.93, 0.99 0.003
## white -0.351 0.162 0.70 0.51, 0.97 0.030
## male 0.043 0.372 1.04 0.50, 2.16 0.91
## married -0.308 0.176 0.74 0.52, 1.04 0.081
## paro -0.108 0.154 0.90 0.66, 1.21 0.48
## numprop 0.276 0.102 1.32 1.08, 1.61 0.007
## crimprop 0.887 0.208 2.43 1.61, 3.65 <0.001
## numarst 0.015 0.007 1.02 1.00, 1.03 0.030
## edcomb -0.049 0.037 0.95 0.88, 1.02 0.19非財産犯に着目したモデルの結果は以下の通り。male、numprop、edcombの3つのみが5%水準で有意で、特にmaleの効果が大きいと推定された。
##
## Variable Coef SE HR 95% CI p-value
## fin 0.004 0.177 1.00 0.71, 1.42 0.98
## age -0.022 0.011 0.98 0.96, 1.00 0.053
## white -0.010 0.174 0.99 0.70, 1.39 0.95
## male 1.44 0.713 4.20 1.04, 17.0 0.044
## married -0.035 0.200 0.97 0.65, 1.43 0.86
## paro -0.279 0.179 0.76 0.53, 1.07 0.12
## numprop 0.258 0.102 1.29 1.06, 1.58 0.012
## crimprop -0.184 0.192 0.83 0.57, 1.21 0.34
## numarst 0.011 0.007 1.01 1.00, 1.02 0.10
## edcomb -0.075 0.037 0.93 0.86, 1.00 0.042二つのモデルで推定された偏回帰係数を比較するために作成したのが表5.4である。競合リスク・モデルの推定値(表5.2)と大きくは変わっていないが、\(z\)統計量の値が少し小さくなっている。一般に、因果推論を行うならば競合リスク・モデルの方がよいとされる。
tibble(Covariate = rownames(mod_subd_prop$coefs %>% data.frame()),
"Coef(prop)" = c(sprintf("%.3f",mod_subd_prop$coefs)[1:10]),
"Exp(Coef_prop)" = c(sprintf("%.3f",exp(mod_subd_prop$coefs))[1:10]),
"Coef(nonprop)" = sprintf("%.3f",mod_subd_nonprop$coefs)[1:10],
"Exp(Coef_nonprop)" = sprintf("%.3f",exp(mod_subd_nonprop$coefs))[1:10]) %>%
flextable() %>%
add_header_row(colwidth = c(1,2,2),
values = c("","財産犯", "非財産犯")) %>%
flextable::align(align = "center", part = "all") %>%
set_caption("各モデルの推定値の比較")財産犯 | 非財産犯 | |||
|---|---|---|---|---|
Covariate | Coef(prop) | Exp(Coef_prop) | Coef(nonprop) | Exp(Coef_nonprop) |
fin | 0.236 | 1.266 | 0.004 | 1.004 |
age | -0.040 | 0.960 | -0.022 | 0.978 |
white | -0.351 | 0.704 | -0.010 | 0.990 |
male | 0.043 | 1.043 | 1.436 | 4.204 |
married | -0.308 | 0.735 | -0.035 | 0.966 |
paro | -0.108 | 0.898 | -0.279 | 0.756 |
numprop | 0.276 | 1.317 | 0.258 | 1.294 |
crimprop | 0.887 | 2.429 | -0.184 | 0.832 |
numarst | 0.015 | 1.015 | 0.011 | 1.011 |
edcomb | -0.049 | 0.952 | -0.075 | 0.928 |
5.3.3 累積発生率関数の予測値
一方で、部分分布を用いたモデルは予測を行う場合には優れているとされる。
時点\(t\)における事象\(j\)の累積発生率関数は以下のように定義される。
\[ F_j(t) = \int_0^t f_j(u)du = \int_0^t h_j(u)S(u)du \]
累積発生率関数の図示はtidycmprskパッケージのcuminc()関数と、ggsurvfitパッケージのggsuminc()関数を利用して行える(図5.4)。
tidycmprsk::cuminc(Surv(arrstday,type2) ~ 1,
rho = 0,
data = tarp) -> pred_cuminc
ggcuminc(pred_cuminc,
outcome = c("1","2"))+
add_confidence_interval()+
theme_bw(base_size = 16)+
scale_linetype_discrete(labels = c("nonprop","prop"))+
theme(aspect.ratio = 1.1)+
scale_x_continuous(breaks = seq(0,350,50))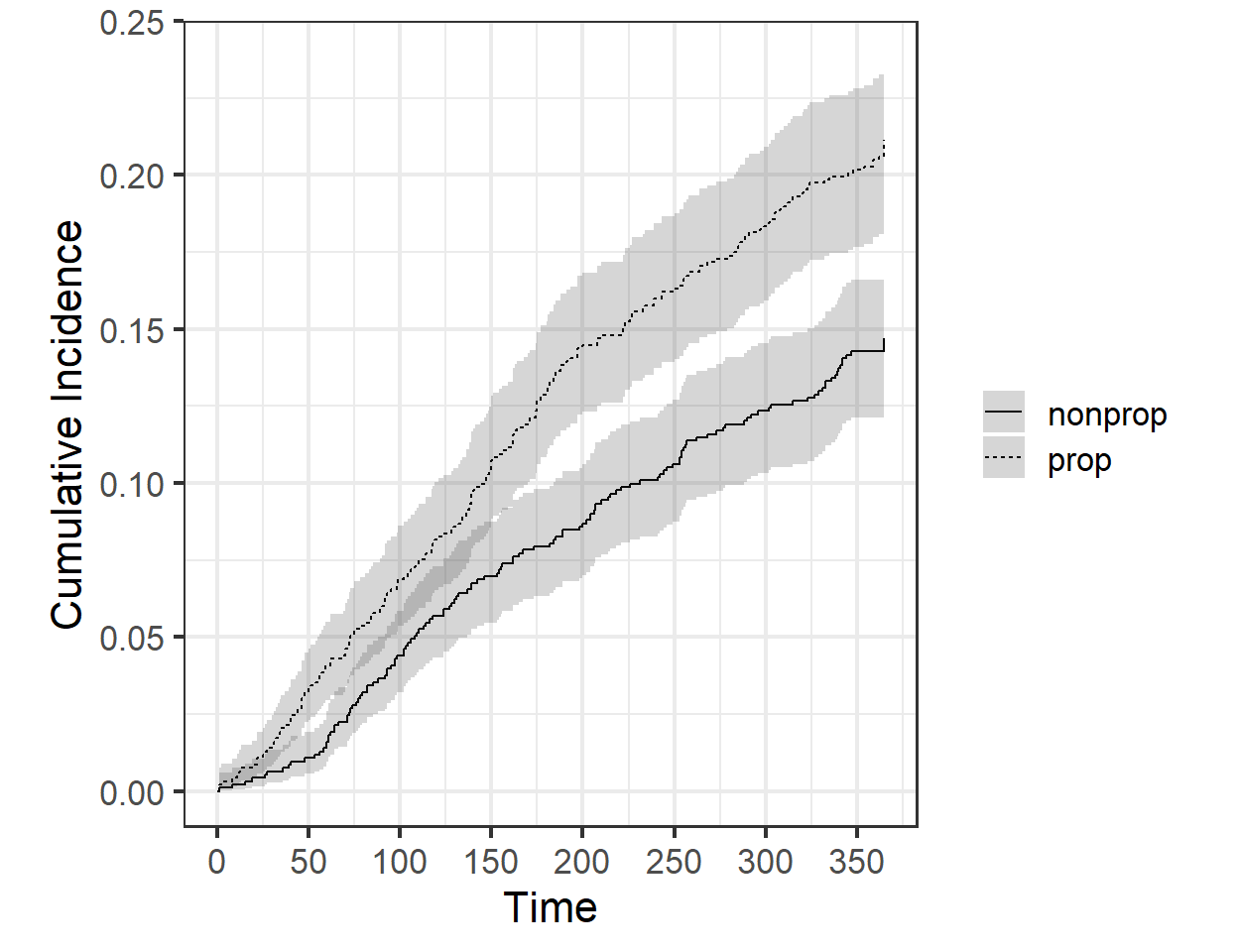
図5.4: 部分分布モデルから推定された累積発生率関数
なお、コックス回帰モデルを使用した競合リスク・モデルも以下のようにすれば累積発生関数を図示できる(図5.5)。しかし、競合リスク・モデルはそれぞれの種類を別々のモデルで推定しているため、両方の予測値を足すと1を超えてしまう場合がある点に注意が必要。
predict_rsk_prop <- survfit(mod_rsk_prop,
conf.int = 0.95)
predict_rsk_nonprop <- survfit(mod_rsk_nonprop,
conf.int = 0.95)
## 財産犯
ggsurvplot(predict_rsk_prop,
data = tarp,
## 塗りつぶしの濃さ
conf.int.alpha = 0.15,
size = 0.5,
## TRUEなら打ち切りデータの場所が明示される
censor = FALSE,
ggtheme = theme_bw(),
## 累積ハザード関数を指定
fun = "cumhaz") -> p_rsk_prop
p_rsk_prop$plot +
theme_bw(base_size = 16)+
labs(x = "week", y = "cumulative hazard", title = "prop")+
theme(legend.position = "none")+
coord_cartesian(xlim = c(0,370), ylim = c(0,0.24))+
scale_x_continuous(breaks = seq(0,350,100))+
theme(aspect.ratio=1.1)-> p_rsk_prop2
## 非財産犯
ggsurvplot(predict_rsk_nonprop,
data = tarp,
## 塗りつぶしの濃さ
conf.int.alpha = 0.15,
size = 0.5,
## TRUEなら打ち切りデータの場所が明示される
censor = FALSE,
ggtheme = theme_bw(),
## 累積ハザード関数を指定
fun = "cumhaz") -> p_rsk_nonprop
p_rsk_nonprop$plot +
theme_bw(base_size = 16)+
labs(x = "week", y = "cumulative hazard", title = "nonprop")+
theme(legend.position = "none")+
coord_cartesian(xlim = c(0,370), ylim = c(0,0.24))+
scale_x_continuous(breaks = seq(0,350,100))+
theme(aspect.ratio=1.1)-> p_rsk_nonprop2
p_rsk_prop2 + p_rsk_nonprop2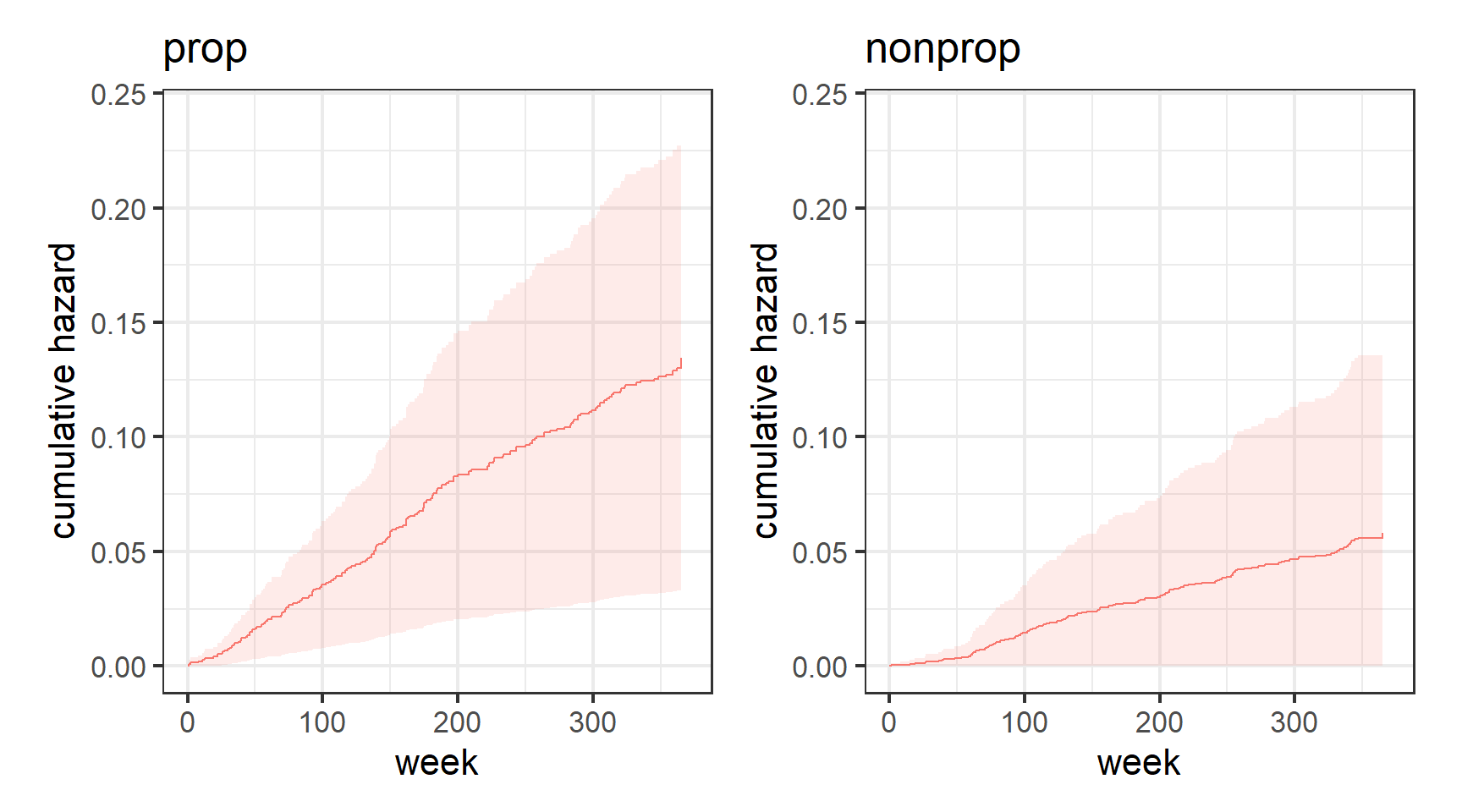
図5.5: 競合リスク・モデルから推定された累積発生関数