1 はじめに

1.1 イベントヒストリー分析とは何か

イベント・ヒストリーとは、研究対象である「個体や集団で、ある事象が生じた時間的な記録」を意味する。霊長類学では、個体が何歳で死亡したかや、オスが何年群れに在籍したかといったデータがこれに該当する。イベント・ヒストリー分析(event history analysis)または生存時間分析(survival analysis)¹は、イベント・ヒステリーを持つデータを用いて、事象の発生パターンや発生の原因を分析する一連の手法である。例えば霊長類の研究では、個体の寿命に影響する要因を調べたり(Ellis et al., 2019; Silk et al., 2010; Thompson & Cords, 2018; Tung et al., 2016)、オスが群れに在籍する確率が時間と共にどう変化するのかを調べたりする(Swedell et al., 2011)ために用いられている。

1.2 イベント・ヒストリー分析の難しさ

イベント・ヒストリーを持つデータの分析が難しい要因としては、扱うデータに以下の2つの特殊性があることが多いことが挙げられる。イベント・ヒストリー分析では、これらの困難に対処するため様々な手法が研究されてきた。

1.2.1 打ち切り

イベント・ヒステリーを持つデータの特殊性の一つは、打ち切りが存在する点である。

具体例として、 Rossi et al. (1980) のデータを見ていこう。この研究では、432名の服役囚が出所後12ヶ月間に再逮捕されるかどうかを調べ、それに年齢や人種、学歴、配偶状態などの要因が影響しているかを調べようとしている。変数の詳細は、こちらを参照。

Rossi <- read_csv("data/Rossi.csv")

Rossi %>% 
  head(20) %>% 
  datatable(options = list(scrollX = 100), rownames = FALSE)

実際にデータからランダムに抽出した20人が再逮捕されたかどうかを見ていこう(図1.1)。arrestは再逮捕されたかどうかを0/1で、weekは再逮捕された場合出所後何週間目だったかを表している。図からわかるように、12ヶ月(52週)経過後も逮捕されていないデータが数多く存在することが分かる。

Rossi %>% 
  sample_n(20) %>% 
  mutate(id = row_number()) %>% 
  mutate(arrest = as.factor(arrest)) %>% 
  ggplot(aes(x = week, y = id))+
  geom_segment(aes(x = 0, xend = week, yend = id, y = id),
               color = "grey")+
  geom_point(shape = 23, size = 3,
             aes(fill = arrest))+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1)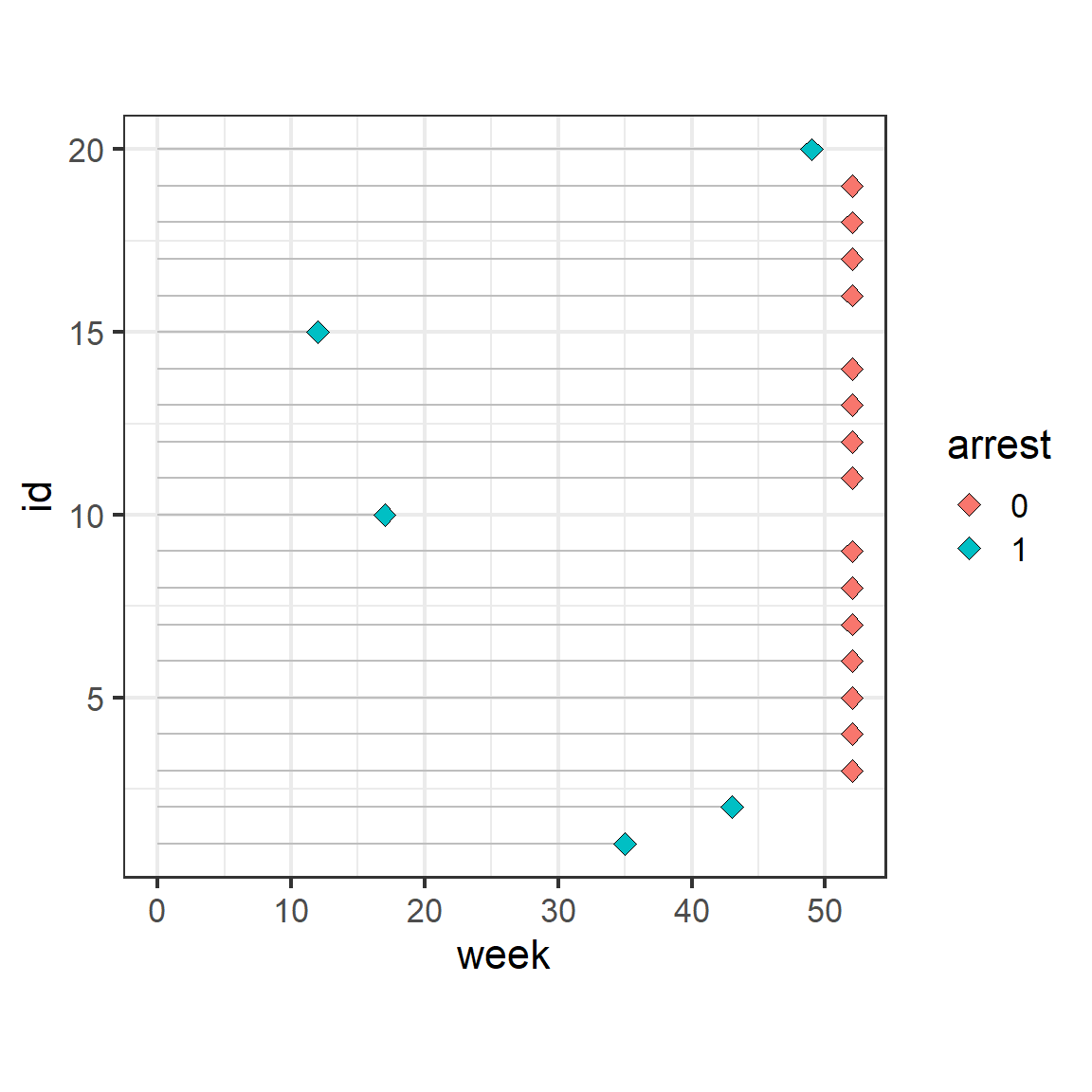

図1.1: 服役囚が出所後何週間で逮捕されたか

このようなデータは、通常の分析ではデータを扱うのが難しい。なぜなら、再逮捕されなかった服役囚に適切に従属変数(応答変数ともいう)²を割り当てることができないからである。彼らは10年たっても再逮捕されなかったかもしれないし、出所後13ヶ月に再逮捕されていたかもしれないが、このデータから知ることは不可能である。彼らに一律に同じ値を割り振っても（例えば期間の最大値である1年を割り振る）、彼らのデータを除外してもデータに大きなバイアスがかかってしまう。

このように、測定値が不完全にしかわからないデータを打ち切りデータという。打ち切りには、上記のように(1)調査終了時点ではまだイベントが起きていない場合と、(2)何らかの事情(e.g., 予期せぬ死、消息不明など)で調査期間の途中でその個体のデータが追跡できなくなっている場合(= 脱落)の2種類が存在する。

1.2.2 時間依存共変量

もう一つの特殊性は、対象の期間中に独立変数(説明変数ともいう)の値が変化する場合があることである（＝時間依存共変量）。

例えば、先ほどの例でも対象の12ヶ月の間に仕事の有無が変化していた(emp1~emp52)。こうした場合、回帰モデルに1ヶ月ごとの仕事の有無（e.g., 1ヶ月目の仕事の有無、2ヶ月目の仕事の有無、…）をすべて独立変数として入れることはできるが、この方法では出所後12ヶ月以内に再逮捕された服役囚に対して独立変数を割り振れないところが出てくる。なぜなら、出所後3ヶ月で再逮捕されたとすると、その服役囚の4ヶ月目以降の仕事のデータはないからである。

1.3 イベント・ヒストリー分析の種類

イベント・ヒストリー分析の手法は以下のような点を基準に分類される。本稿では、まず単純なモデルの説明から始め、徐々に難しいモデルの説明へ移る。

1.3.1 繰り返しの有無

生物学で扱うことの多い「死」という事象は一個体に一度しか生じないが、転職や結婚といった事象を扱う場合、これらは個人の一生において何度も発生する可能性がある。繰り返しの阿辻賞を扱う際にはより複雑な分析モデルが必要になる。

1.3.2 単一の事象と複数の事象

例えば生物の生死を扱うとき、多くの場合では死亡のタイプ（e.g., 死因など）を区別せず単一の死亡として扱う。しかし、死亡のタイプを分けて分析を行うことも可能である。このような複数の事象を扱うためには、単一な事象を扱う分析よりも複雑なモデルが必要である。

1.3.3 パラメトリック法とノンパラメトリック法

分析には、事象の発生時間の分布（どのような時間間隔で事象が発生するか）に仮定を置かないノンパラメトリックな分析と、特定の分布族（e.g., 指数分布、ワイブル分布など）を仮定するパラメトリックな分析がある。また、これら2つを結合したCoxの比例ハザードモデルは事象の発生時間に特定の分布を仮定しないが、線形関数に基づく回帰モデルであるというという点でセミパラメトリックな手法であるといえる。

1.3.4 離散時間と連続時間

事象の発生時間が正確に記録できている場合は「連続時間」モデルといわれる。通常は、時間の測定単位が小さい場合は（時間、分、秒）、連続時間として扱ってよい。一方、時間の測定単位が大きい場合（月、年）は「離散時間」モデルで扱うのが適している。実際の分析では離散時間モデルの方が理解するのが容易である。

References

Ellis, S., Snyder-Mackler, N., Ruiz-Lambides, A., Platt, M. L., & Brent, L. J. N. (2019). Deconstructing sociality: The types of social connections that predict longevity in a group-living primate. Proc. Biol. Sci., 286(1917), 20191991.

Rossi, P. H., Berk, R. A., & Lenihan, K. J. (1980). Money, work and crime: Some experimental results. New York: Academic Press.

Silk, J. B., Beehner, J. C., Bergman, T. J., Crockford, C., Engh, A. L., Moscovice, L. R., Wittig, R. M., Seyfarth, R. M., & Cheney, D. L. (2010). Strong and consistent social bonds enhance the longevity of female baboons. Curr. Biol., 20(15), 1359–1361.

Swedell, L., Saunders, J., Schreier, A., Davis, B., Tesfaye, T., & Pines, M. (2011). Female “dispersal” in hamadryas baboons: Transfer among social units in a multilevel society. Am. J. Phys. Anthropol., 145(3), 360–370.

Thompson, N. A., & Cords, M. (2018). Stronger social bonds do not always predict greater longevity in a gregarious primate. Ecol. Evol., 8(3), 1604–1614.

Tung, J., Archie, E. A., Altmann, J., & Alberts, S. C. (2016). Cumulative early life adversity predicts longevity in wild baboons. Nat. Commun., 7.

このような分析手法は様々な分野で発展してきたため、分野ごとに呼ばれ方が異なる。例えば生物学では動物の寿命を扱うことが多いため「生存時間分析」、工学の分野では機械の故障を扱うことが多いため「故障時間分析」などと呼ばれる。「イベント・ヒストリー分析」という呼び方は、こうした様々な分野で発展した分析手法の包括的な呼称である。↩︎
従属変数、独立変数がわからない場合はこちらを参照。↩︎