4 コックス回帰モデル

前章(3)で解説したパラメトリックモデルは非常に有効である一方で以下の2点の欠点もあった。

1. 最も適切な分布を決めなくてはならず、それがしばしば難しい
   
2. 時間依存的な独立変数を使うことができない

コックスの比例ハザードモデル(Cox, 1972) (コックス回帰モデル)はこうした欠点をどちらも解決してくれる優れた分析手法である。

4.1 比例ハザードモデル

4.1.1 モデルの概要

コックス回帰モデルはこれまで説明したパラメトリックな比例ハザードモデルを一般化したものといえる。ひとまず、非時間依存な独立変数2つを持つモデルを考えると、比例ハザードモデルは以下のように書ける(式(4.1))。ここで、\(a(t)\)は時間の関数であり、どんな形でもよい。この形を一定の形に決める必要がないので、このモデルはしばしば「セミパラメトリック」なモデルと呼ばれる¹¹。

\[ log(h(t)) = a(t) + b_1x_1 + b_2x_2 \tag{4.1} \]

任意の時間\(t\)に対して、個体\(i\)と\(j\)のハザード比(\(h_i(t)/h_j(t)\))の値が一定なので比例ハザードモデルといわれている。個体Aのハザード率を\(h_A(t)\)、個体\(B\)のハザード率を\(h_B(t)\)とするとき、式(4.1)より以下のように導ける。このように、ハザード比は\(t\)に依らず一定になる。
\[ \begin{align} \frac{h_A(t)}{h_B(t)} &= \frac{exp(a(t) + b_1x_{1A} + b_2x_{2A})}{exp(a(t) + b_1x_{1A} + b_2x_{2B})}\\ &= \frac{e^{a(t)} \times e^{b_1} \times e^{x_{1A}} \times e^{b_2} \times e^{x_{2A}}}{e^{a(t)} \times e^{b_1} \times e^{x_{1B}} \times e^{b_2} \times e^{x_{2B}}}\\ &= \frac{e^{x_{1A}+x_{2A}}}{e^{x_{1B}+x_{2B}}} \end{align} \]

第3章のパラメトリックなモデルはコックス回帰モデルの特殊例である。\(a(t)\)が定数なら指数分布モデル、\(a(t) = ct\)ならワイブル回帰モデルになる。\(a(t)\)はいかなる形も取れるので、例えば以下のような4次の多項式にすることもできる(式(4.2))。

\[ a(t) = a_0 + a_1t + a_2t^2 + a_3t^3 + a_4t^4 \tag{4.2} \]

4.1.2 部分尤度法

コックス回帰モデルでは部分尤度法と呼ばれる方法でパラメータの推定を行う。この方法では、尤度関数を偏回帰係数(\(b_1,b_2\))のみを含む部分と偏回帰係数と関数\(a(t)\)の両方を含む部分に分解し、前者のみに着目して通常のパラメータ推定を行う。つまり、時間\(t\)に依存する部分を無視して偏回帰係数のみを推定できるのである。部分尤度法では正確な事象の発生時間ではなく、事象の発生順序のみに基づいて推定が行われるため、時間を二乗したり整数倍しても推定結果は変わらない。詳しい解説は Allison (2014) を参照。

4.1.3 Rによる実装

第3章で分析した元服役囚の再犯データにコックス回帰モデルを当てはめる。分析には、survivalパッケージのcoxph()関数を使用する。

mod_cox <- coxph(Surv(week, arrest) ~ fin + age + race + wexp + mar 
                 + paro + prio, data = recid)

結果は以下の通り。係数の推定値自体はワイブル回帰モデルとほとんど変わらない(表3.3参照)。指数変換された標準偏回帰係数はパラメトリックなモデルと同様にハザード比として解釈できる。例えば、経済的支援を受けた元服役囚は受けてない元服役囚よりも再犯の可能性が約32%低下することが分かる。

mod_cox

## Call:
## coxph(formula = Surv(week, arrest) ~ fin + age + race + wexp + 
##     mar + paro + prio, data = recid)
## 
##          coef exp(coef) se(coef)      z       p
## fin  -0.37942   0.68426  0.19138 -1.983 0.04742
## age  -0.05744   0.94418  0.02200 -2.611 0.00903
## race  0.31390   1.36875  0.30799  1.019 0.30812
## wexp -0.14980   0.86088  0.21222 -0.706 0.48029
## mar  -0.43370   0.64810  0.38187 -1.136 0.25606
## paro -0.08487   0.91863  0.19576 -0.434 0.66461
## prio  0.09150   1.09581  0.02865  3.194 0.00140
## 
## Likelihood ratio test=33.27  on 7 df, p=2.362e-05
## n= 432, number of events= 114

survminerパッケージのggforest()関数で結果を図示することもできる(図4.1)。推定されたハザード比と95%信頼区間、検定結果が示されている。

ggforest(mod_cox)

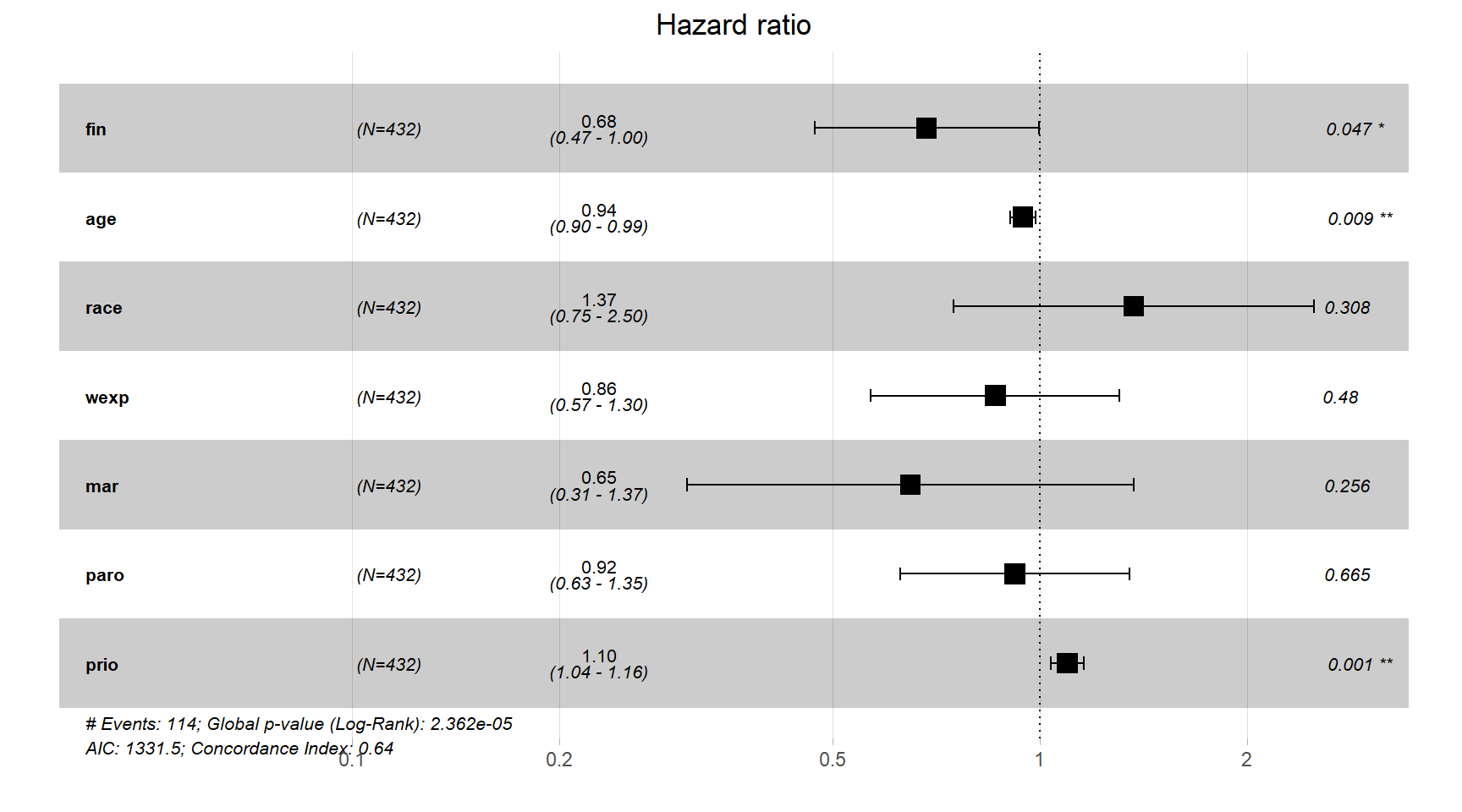
図4.1: mod_coxで推定されたハザード比

4.2 時間に依存する独立変数を含むコックス回帰

4.2.1 モデルの概要

コックス回帰モデルは時間依存的な独立変数を含むモデルに拡張できる(式(4.3))。

\[ log(h(t)) = a(t) + b_1x_1 + b_2x_2(t) \tag{4.3} \]

独立変数の値の変化とそれがハザード率に与える影響の間にタイムラグがある場合は、例えば以下のように1週間前の値を独立変数にするようにモデリングすることもできる(式(4.4))。

\[ log(h(t)) = a(t) + b_1x_1 + b_2x_2(t-1) \tag{4.4} 　　 \]

4.2.2 Rでの実装

再犯データのモデルの独立変数に、各週の就業状況(work)を加えてモデリングを行う。Rで分析を行う際には、それぞれの人の各週のデータすべてが1行ずつあるようなデータフレームを作成する必要がある。

recid %>% 
  rownames_to_column(var = "id") %>% 
  ### 就業状態を一列に
  pivot_longer(cols = work1:work52,
               names_to = "work_week",
               values_to = "work",
               values_drop_na = TRUE) %>% 
  arrange(id) %>% 
  group_by(id) %>%
  ## 各行データの観察開始時点
  mutate(start = 1:n() -1) %>% 
  ## 各行データの観察終了時点(何週目か)  
  mutate(stop = 1:n()) %>% 
  ## 再犯があった州のarrestのみを1にして、そのほかは0にする  
  mutate(arrest = ifelse(arrest == 1 & week == stop,1,0)) %>% 
  ##1週前の就業状態  
  mutate(worklag = lag(work,1))-> recid_long

それでは、時間依存変数を含んだコックス回帰モデルを実行する。まずは式(4.3)のモデルを推定する。従属変数は、Surv(start, stop, arrest)となる点に注意。

mod_cox_ti <- coxph(Surv(start, stop, arrest) ~ fin + age + race + wexp + mar 
                 + paro + prio + work, data = recid_long)

結果は以下の通り。

mod_cox_ti

## Call:
## coxph(formula = Surv(start, stop, arrest) ~ fin + age + race + 
##     wexp + mar + paro + prio + work, data = recid_long)
## 
##          coef exp(coef) se(coef)      z        p
## fin  -0.35672   0.69997  0.19113 -1.866  0.06198
## age  -0.04634   0.95472  0.02174 -2.132  0.03301
## race  0.33866   1.40306  0.30960  1.094  0.27402
## wexp -0.02555   0.97477  0.21142 -0.121  0.90380
## mar  -0.29375   0.74546  0.38303 -0.767  0.44314
## paro -0.06421   0.93781  0.19468 -0.330  0.74156
## prio  0.08514   1.08887  0.02896  2.940  0.00328
## work -1.32832   0.26492  0.25072 -5.298 1.17e-07
## 
## Likelihood ratio test=68.65  on 8 df, p=9.114e-12
## n= 19809, number of events= 114

ggforest()関数によって図示した結果が図4.2である。

ggforest(mod_cox_ti)

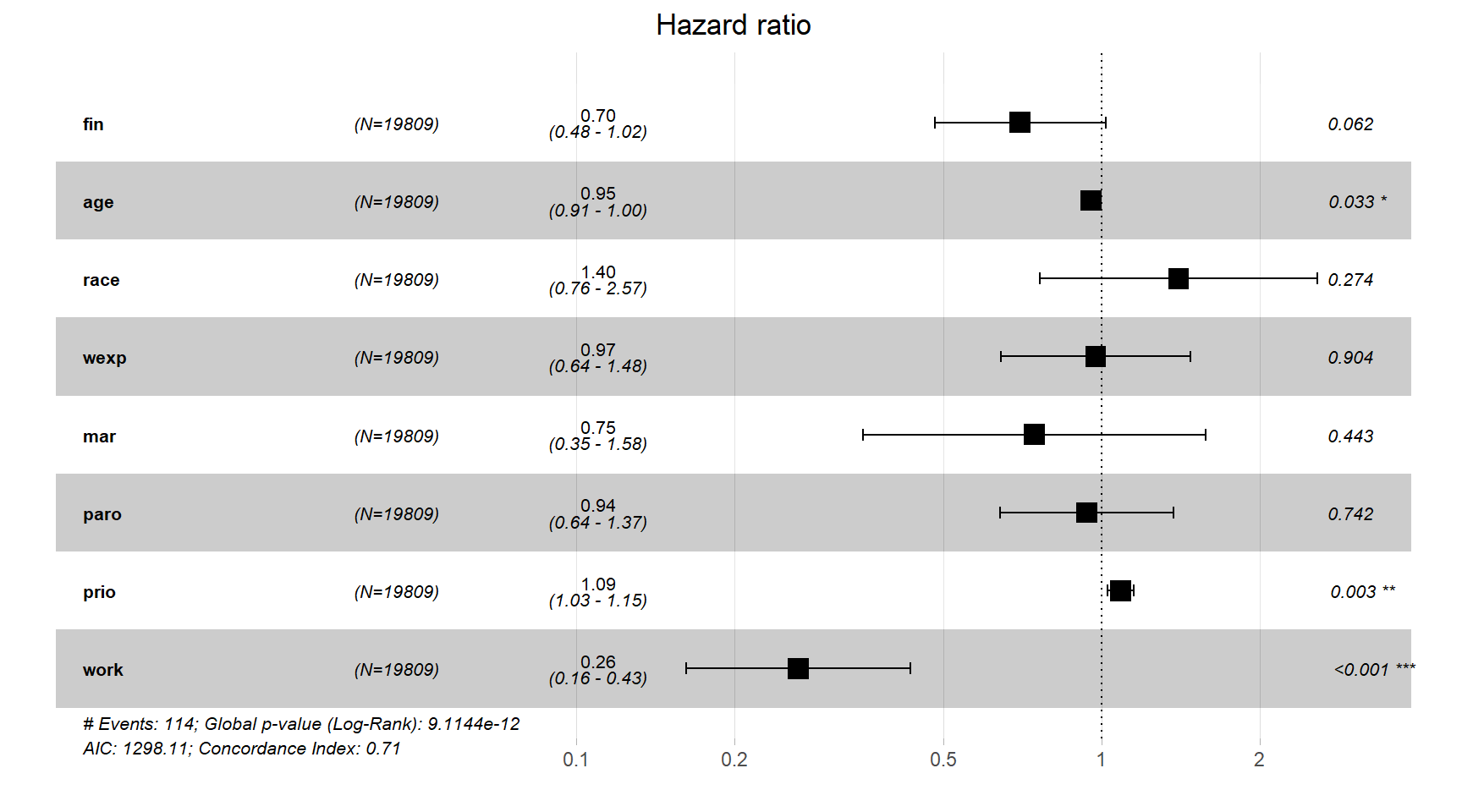
図4.2: mod_coxで推定されたハザード比

続いて、式(4.4)のモデルを推定する。workの代わりにworklagを説明変数に入れる。

mod_cox_tlag <- coxph(Surv(start, stop, arrest) ~ fin + age + race + wexp + mar 
                 + paro + prio + worklag, data = recid_long)

結果は以下の通り。

mod_cox_tlag

## Call:
## coxph(formula = Surv(start, stop, arrest) ~ fin + age + race + 
##     wexp + mar + paro + prio + worklag, data = recid_long)
## 
##             coef exp(coef) se(coef)      z        p
## fin     -0.35130   0.70377  0.19181 -1.831 0.067035
## age     -0.04977   0.95144  0.02189 -2.274 0.022969
## race     0.32147   1.37915  0.30912  1.040 0.298369
## wexp    -0.04764   0.95348  0.21323 -0.223 0.823207
## mar     -0.34476   0.70839  0.38322 -0.900 0.368310
## paro    -0.04710   0.95399  0.19630 -0.240 0.810375
## prio     0.09199   1.09635  0.02880  3.194 0.001402
## worklag -0.78689   0.45526  0.21808 -3.608 0.000308
## 
## Likelihood ratio test=47.16  on 8 df, p=1.43e-07
## n= 19377, number of events= 113 
##    (432 observations deleted due to missingness)

ggforest()関数によって図示した結果が図4.3である。

ggforest(mod_cox_tlag)

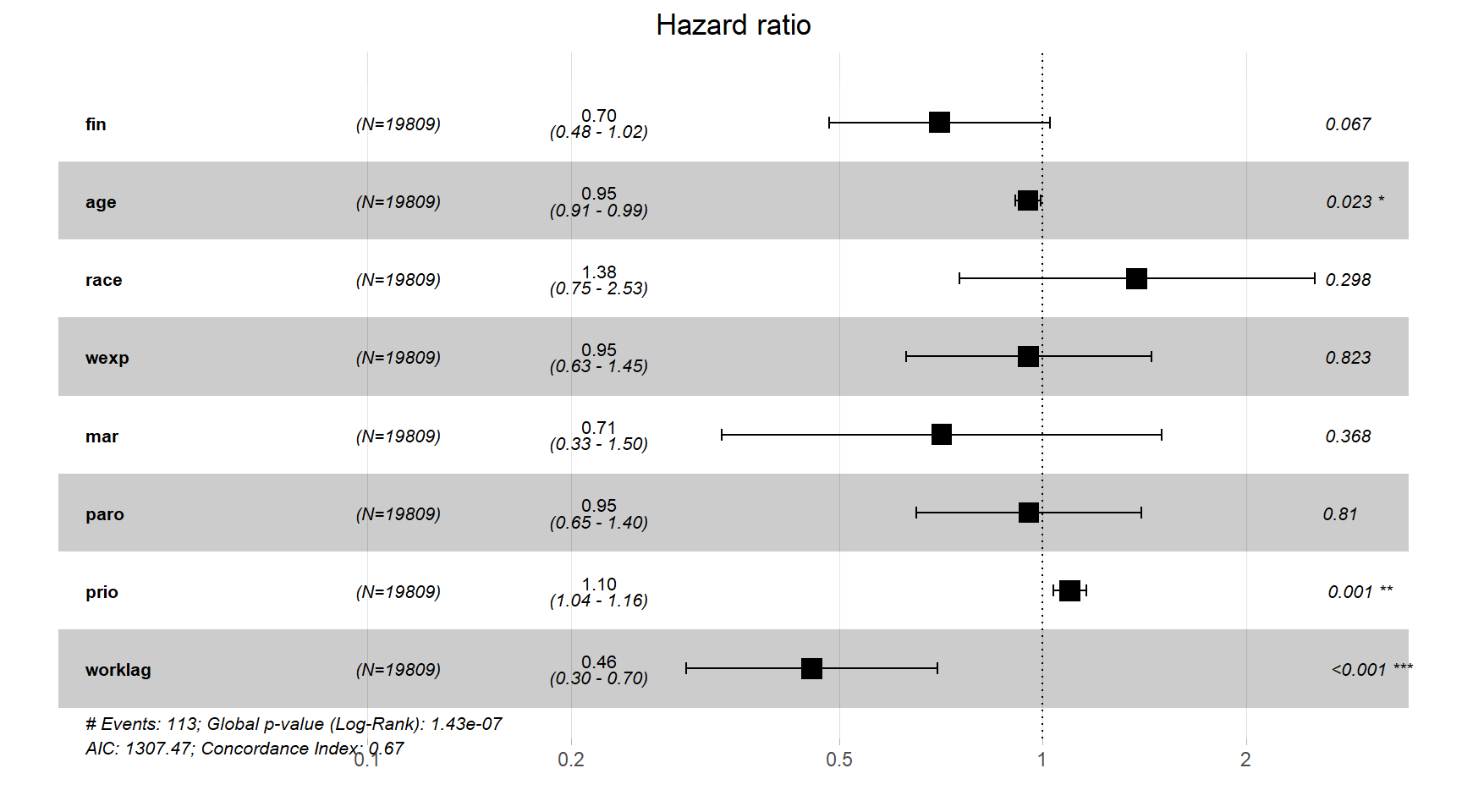
図4.3: mod_coxで推定されたハザード比

4.2.3 モデルの比較

推定した3つのモデルの推定値をまとめたものが表4.1である。推定結果自体は非常によく似ているが、先ほどの検定結果を見ると経済的支援の効果は時間依存変数を含まない基本モデルのみで有意になっている。また、時間依存変数の就業状態(workまたはworklag)が他の変数よりも大きな影響を与えていたことも分かった。、2つ目のモデルのハザード比(Exp(Coef) = 0.265)をみると就業している元服役囚の再犯率が就業していない服役囚の26.5%であると推定された。

ただし、この結果のみでは就業状態が再犯に影響したのか、再犯が就業状態に影響したのかはわからない。そこで、就業状態に1週間のラグがあるモデル3の結果を見ると、2つ目のモデルより効果量は減少するものの、依然として大きな影響を及ぼしていることが分かる。モデル3のハザード比(Exp(Coef) = 0.455)から、就業状態にある元服役囚はそうでない元服役囚に比べて翌週の再犯率が約54.5%低いことが分かる。このように、タイムラグを持つ変数を用いることで再犯が就業状態に影響する可能性を除外することができる。

tibble(Covariate = rownames(mod_cox_ti$coefficients %>% data.frame()),
       "Coef(basic)" = c(sprintf("%.3f",coef(mod_cox))[1:7],NA),
       "Exp(Coef_basic)" = c(sprintf("%.3f",exp(coef(mod_cox)))[1:7],NA),
       "Coef(ti)" = sprintf("%.3f",coef(mod_cox_ti))[1:8],
       "Exp(Coef_ti)" = sprintf("%.3f",exp(coef(mod_cox_ti)))[1:8],
       "Coef(tlag)" = sprintf("%.3f",coef(mod_cox_tlag))[1:8],
       "Exp(Coef_tlag)" = sprintf("%.3f",exp(coef(mod_cox_tlag))[1:8])) %>% 
  mutate(Covariate = ifelse(str_detect(Covariate,"work"),"work/worklag",Covariate)) %>% 
  flextable() %>% 
  add_header_row(colwidth = c(1,2,2,2),
                 values = c("","基本モデル","時間依存独立変数\nあり", "タイムラグのある\n時間独立変数あり")) %>% 
  flextable::align(align = "center", part = "all") %>% 
  set_caption("各モデルの推定値の比較")

表4.1: 各モデルの推定値の比較

	基本モデル		時間依存独立変数 あり		タイムラグのある 時間独立変数あり
Covariate	Coef(basic)	Exp(Coef_basic)	Coef(ti)	Exp(Coef_ti)	Coef(tlag)	Exp(Coef_tlag)
fin	-0.379	0.684	-0.357	0.700	-0.351	0.704
age	-0.057	0.944	-0.046	0.955	-0.050	0.951
race	0.314	1.369	0.339	1.403	0.321	1.379
wexp	-0.150	0.861	-0.026	0.975	-0.048	0.953
mar	-0.434	0.648	-0.294	0.745	-0.345	0.708
paro	-0.085	0.919	-0.064	0.938	-0.047	0.954
prio	0.091	1.096	0.085	1.089	0.092	1.096
work/worklag			-1.328	0.265	-0.787	0.455

4.2.4 データに欠損がある場合の補完と加工

時間依存独立変数があるモデルの推定をするとき、ある時点で事象が発生した場合、その時点で事象を経験しうるすべての個体について時間依存変数の値が分かっていなければいけない。例えば、\(t =10\)で事象が発生し、その時点で15人が事象を経験する可能性がある(= リスク集合にいる)場合、15人全員について\(t=10\)時点の時間依存変数が分かっていなければいけない。そのため、事象の発生が日単位で測定されているにもかかわらず、時間依存変数の値が1週間ごとにしか測定されていないといったことがあるとき、問題が生じることになる。

このような場合、特定の方法で事象が発生した時点の独立変数の値を補完して代入する必要がある。いろいろな方法があるが、最も安全なものは直前に観察された値を使用する方法である。保管によって必要な代入ができたら、次に分析のためにデータを加工する必要がある。加工方法には以下の2つがあるが、統計ソフトではいずれかを使用している(Rはエピソード分割法)。どちらも選べるならば後者の方が望ましい。

4.2.4.1 プログラミング・ステートメント法(programming statements method)

この方法を使用するには、データをワイド形式にする必要がある。すなわち、今回の例では各週の就業状態が1列ずつになるようにする必要がある。

4.2.4.2 エピソード分割法(episode splitting method)

この方法のデータは先ほど加工したrecid_longのようにロング形式で問題ない。それぞれの個体が複数の行を持ち、各行のデータについて観察し始めた時点(start)と観察が終了した時点(stop)を記した列を作る。また独立変数が変化するたびに行を変えるか、もしくは独立変数の変化に関係なく小さな時間間隔ごとに行を変える(どちらでも問題ない)。例えばrecid_longでは各個体が1週間ごとに1行ずつのデータを持つ。

recid_long %>% 
  head(50) %>% 
  datatable(options = list(scrollX = 20))

4.3 比例ハザード性の仮定の検討と修正

4.3.1 シェーンフィールド残差を用いた検討

コックス回帰モデルの仮定として、どの時点でも2個体のハザード比が一定であるとする「比例ハザード性」があった。この仮定が満たされないときはどのようなときだろうか?

ハザード比が一定になるのは、ハザード率の対数に対して各独立変数の影響が全ての時点で同じときである。そのため、時間と独立変数に交互作用があるときはハザード率の比は一定にならない。式(4.5)はその一例である。この式で独立変数\(x\)がハザード率の対数に与える影響は\(b + ct\)なので、時間と共に増加/減少する。

\[ log(h(t)) = a(t) + bx + cxt \tag{4.5} \]

比例ハザード性を検討する方法はいくつかあるが、最も簡便なものはシェーンフィールド残差を用いる方法である。子の残差は独立変数の一つ一つに対して研鑽され、比例ハザード性が満たされるならば時間、あるいは時間の関数と相関がない。

Rでシェーンフィールド残差を調べるためには、以下のようなコードを実行する。ここでは、2つ目のモデル(mod_cox_ti)について分析を行う。chisqの列には「相関係数が0である」を帰無仮説とする検定を行った際のカイ二乗値が、pにはp値が示されている。年齢(age)はp値が0.05を下回っており、比例ハザード性の仮定を満たしていない可能性が示唆された。一番下には「全ての相関係数が0である」を帰無仮説とする包括的検定(GLOBAL)が行われており、これも5%水準で有意である。

cox.zph(mod_cox_ti, transform = "identity") 

##          chisq df     p
## fin     0.0143  1 0.905
## age     6.5021  1 0.011
## race    1.9489  1 0.163
## wexp    3.5032  1 0.061
## mar     0.8508  1 0.356
## paro    0.0118  1 0.913
## prio    0.3363  1 0.562
## work    0.1972  1 0.657
## GLOBAL 17.1128  8 0.029

survminerパッケージのggcoxzphをもちいて視覚的に仮定をチェックすることもできる(図4.4)。

ggcoxzph(cox.zph(mod_cox_ti, transform = "identity") )

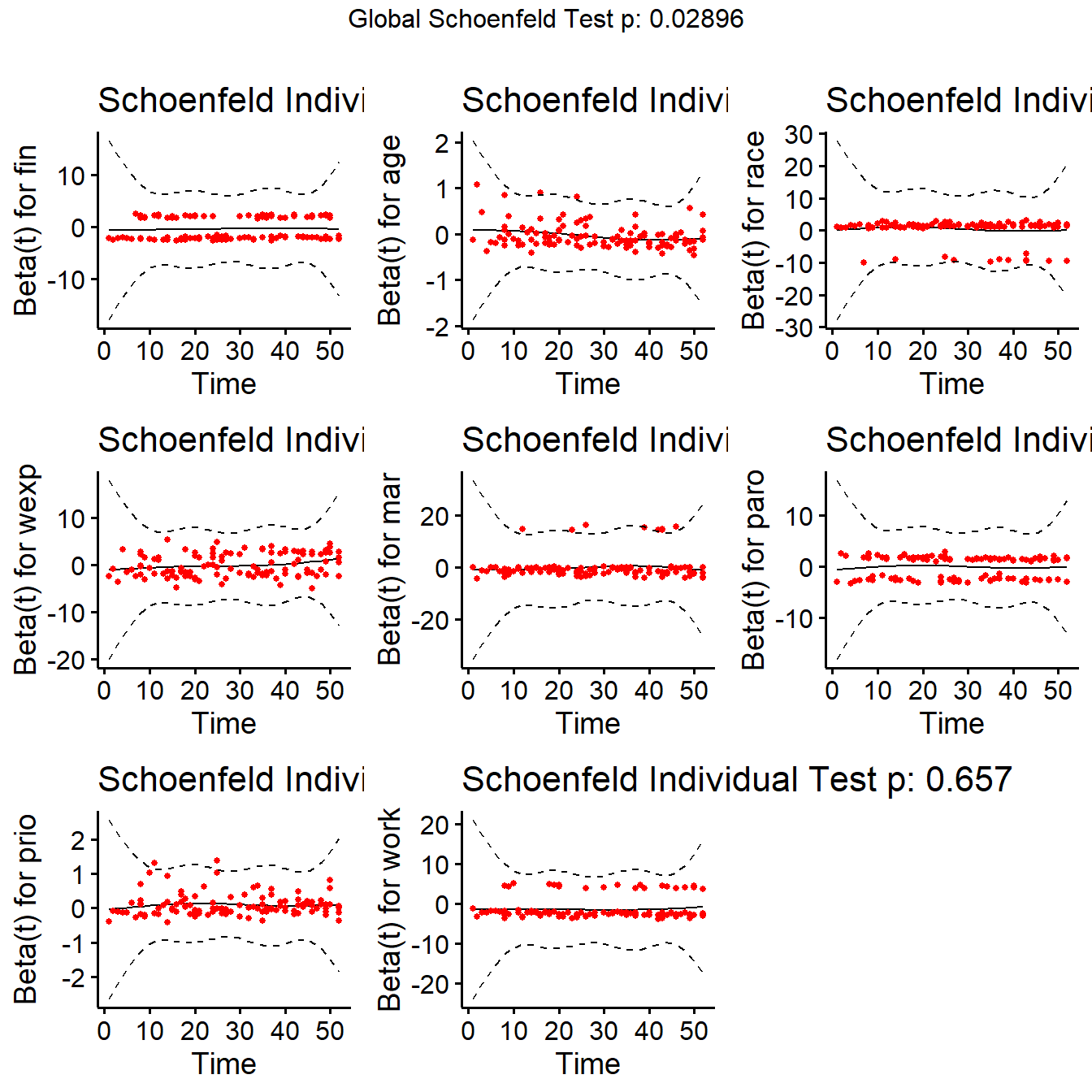
図4.4: 各独立変数の比例ハザード性のチェック

なお、比例ハザード性が満たされるためには実際は時間そのものだけではなく、時間の関数(時間の対数や順位、および事象が発生した時間の累積分布関数の推定値など)とも無相関である必要である。Rでは、時間の順位と、Kaplan-meiyer法による生存確率の推定値(後述)との相関も調べることができる。結果はほとんど変わらない。

## 時間
cox.zph(mod_cox_ti, transform = "rank") 

##          chisq df      p
## fin     0.0181  1 0.8929
## age     6.7334  1 0.0095
## race    1.9342  1 0.1643
## wexp    3.3284  1 0.0681
## mar     0.8976  1 0.3434
## paro    0.0166  1 0.8975
## prio    0.2838  1 0.5942
## work    0.1756  1 0.6752
## GLOBAL 17.1526  8 0.0286

## 生存確率の推定値
cox.zph(mod_cox_ti, transform = "km") 

##           chisq df     p
## fin    9.58e-04  1 0.975
## age    5.89e+00  1 0.015
## race   1.87e+00  1 0.171
## wexp   3.83e+00  1 0.050
## mar    8.29e-01  1 0.363
## paro   5.64e-03  1 0.940
## prio   4.27e-01  1 0.514
## work   2.50e-01  1 0.617
## GLOBAL 1.66e+01  8 0.034

4.3.2 仮定が満たされないときの修正

4.3.2.1 時間との交互作用をモデルに加える

仮定が満たされないときの解決策の一つは独立変数と時間の交互作用を含んだ式(4.5)のようなモデルを推定することである。コックス回帰モデルのすばらしさは、このように比例ハザード性を持たないモデルを柔軟に修正できる点である。ここでは、p値が0.1以下だった年齢(age)と過去の就業経験(wexp)について各データポイント時点の週(stop)との交互作用を入れたモデルを検討する。

mod_cox_int <- coxph(Surv(start, stop, arrest) ~ fin + age + race + wexp + mar 
                 + paro + prio + work + age:stop + wexp:stop, data = recid_long)

結果は以下の通りである。いずれの交互作用も有意な影響を持っていることが分かる。

mod_cox_int

## Call:
## coxph(formula = Surv(start, stop, arrest) ~ fin + age + race + 
##     wexp + mar + paro + prio + work + age:stop + wexp:stop, data = recid_long)
## 
##                coef exp(coef)  se(coef)      z        p
## fin       -0.361738  0.696465  0.190891 -1.895 0.058093
## age        0.085368  1.089118  0.040598  2.103 0.035484
## race       0.305627  1.357476  0.309442  0.988 0.323313
## wexp      -1.209155  0.298449  0.481342 -2.512 0.012003
## mar       -0.233974  0.791382  0.383910 -0.609 0.542226
## paro      -0.063033  0.938913  0.194910 -0.323 0.746398
## prio       0.080920  1.084284  0.028951  2.795 0.005188
## work      -1.318052  0.267656  0.251332 -5.244 1.57e-07
## age:stop  -0.005091  0.994922  0.001541 -3.304 0.000952
## wexp:stop  0.041276  1.042139  0.014512  2.844 0.004451
## 
## Likelihood ratio test=83.62  on 10 df, p=9.751e-14
## n= 19809, number of events= 114

交互作用項については、一般化線形モデルなどと同様に解釈することができる¹²。式(4.5)を書き換えると以下のように書ける。

\[ log(h(t)) = a(t) + (b+ct)x \]

ここからわかるように、独立変数\(x\)が1増えると、ハザード関数の対数は\(b+ct\)増える。つまり、\(x\)の「効果」は時間の線形関数になっていて、\(t=0\)のときは\(b\)でそこから時間が１単位増えるごとに効果が\(c\)ずつ増えていくということになる。例えば先ほどの推定結果から、就業経験の有無の効果は\(-1.21 + 0.041 \times t\)となり、効果が1週ごとに\(0.041\)ずつ増加することが分かる。表4.2は、出所時の年齢(age)と就業経験の有無(wexp)の効果が時間がたつにつれてどのように変化すると推定されたかを示している。例えばwexpについては、出所直後は就業経験があるとない場合に比べてハザード率が29.8%になることが分かるが、50週後にはむしろ就業経験があるとない場合に比べてハザード比が235%上昇することが分かり、このような効果の逆転は30週くらいで起こっていることが分かる。

tibble(t = seq(0,50,10),
       `偏回帰係数\n(b + ct)` = sprintf("%.3f",mod_cox_int$coefficients[[2]] + mod_cox_int$coefficients[[9]]*t),
         `Exp(b+ct)` = sprintf("%.3f", exp(mod_cox_int$coefficients[[2]] + mod_cox_int$coefficients[[9]]*t)),
       `偏回帰係数\n(b + ct) ` = sprintf("%.3f", mod_cox_int$coefficients[[4]] + mod_cox_int$coefficients[[10]]*t),
         `Exp(b+ct) ` = sprintf("%.3f", exp(mod_cox_int$coefficients[[4]] + mod_cox_int$coefficients[[10]]*t))) %>% 
  rename(`出所して\nからの週(t)` = t) %>% 
  flextable() %>% 
  width(width = 2/2) %>% 
  add_header_row(colwidth = c(1,2,2),
                 values = c("","出所時の年齢","就業経験の有無")) %>% 
  flextable::align(align = "center", part = "all")  %>% 
  set_caption("モデルから推定された交互作用項を含む偏回帰係数")

表4.2: モデルから推定された交互作用項を含む偏回帰係数

	出所時の年齢		就業経験の有無
出所して からの週(t)	偏回帰係数 (b + ct)	Exp(b+ct)	偏回帰係数 (b + ct)	Exp(b+ct)
0	0.085	1.089	-1.209	0.298
10	0.034	1.035	-0.796	0.451
20	-0.016	0.984	-0.384	0.681
30	-0.067	0.935	0.029	1.030
40	-0.118	0.888	0.442	1.556
50	-0.169	0.844	0.855	2.350

交互作用モデルでは、全ての独立変数についてモデルのシェーンフィールド残差と時間の相関がなくなっていることが分かる。

cox.zph(mod_cox_int)

##            chisq df    p
## fin       0.0290  1 0.86
## age       2.4002  1 0.12
## race      1.5400  1 0.21
## wexp      2.6158  1 0.11
## mar       0.6847  1 0.41
## paro      0.1608  1 0.69
## prio      0.0111  1 0.92
## work      0.2701  1 0.60
## age:stop  0.4199  1 0.52
## wexp:stop 1.5229  1 0.22
## GLOBAL    6.6780 10 0.76

交互作用モデルの欠点は、交互作用項をパラメトリックな特定の形で定式化する必要がある点である。ただし、これまで時間と独立変数は一次の線形関係にあるとしていたが、代わりに時間の二乗や対数変換した時間をモデルに含めることも可能である。

4.3.2.2 層化(stratification)

もう一つの方法が層化という方法で、就業経験のような離散的な変数が比例ハザード性を満たさないときに使える。

例えば就業経験について層化を行うとすると、就業経験のある元服役囚のデータのみを含むモデルと、就業経験のない元服役囚のデータのみを含むモデルの2つを考える。いずれも同じ偏回帰係数を持つが、時間の関数の形が異なる。時間tにおける就業経験の効果は\(a_1(t) - a_2(t)\)であり、いかなる制約も比例ハザード性も仮定していない。しかし、部分尤度法を用いる以上これを推定することはできない。

\[ \begin{aligned} 就業経験あり: log(h(t)) &= a_1(t) + b_1x_1 + b_2x_2 + ...\\ 就業経験なし: log(h(t)) &= a_2(t) + b_1x_1 + b_2x_2 + ... \end{aligned} \]

層化モデルは、Rで以下のように実行できる。

mod_cox_str <- coxph(Surv(start, stop, arrest) ~ fin + age + race + mar 
                 + paro + prio + work + strata(wexp), data = recid_long)

結果は以下の通り。層化したことで、就業経験の偏回帰係数がなくなる。このように、層化するとその独立変数の効果は推定できなくなる。

mod_cox_str  

## Call:
## coxph(formula = Surv(start, stop, arrest) ~ fin + age + race + 
##     mar + paro + prio + work + strata(wexp), data = recid_long)
## 
##          coef exp(coef) se(coef)      z       p
## fin  -0.35910   0.69831  0.19121 -1.878 0.06038
## age  -0.04766   0.95346  0.02192 -2.174 0.02969
## race  0.34453   1.41133  0.30963  1.113 0.26583
## mar  -0.30368   0.73810  0.38355 -0.792 0.42850
## paro -0.06255   0.93937  0.19477 -0.321 0.74811
## prio  0.08419   1.08784  0.02905  2.898 0.00375
## work -1.32825   0.26494  0.25091 -5.294 1.2e-07
## 
## Likelihood ratio test=59.08  on 7 df, p=2.307e-10
## n= 19809, number of events= 114

交互作用モデルと層化モデルの偏回帰係数を比較したのが表4.3である。推定結果に少し違いがみられる。

tibble(Covariate = rownames(mod_cox_int$coefficients %>% data.frame()),
       "Coef(int)" = c(sprintf("%.3f",coef(mod_cox_int))[1:10]),
       "Exp(Coef_int)" = c(sprintf("%.3f",exp(coef(mod_cox_int)))[1:10]),
       "Coef(str)" = c(sprintf("%.3f",coef(mod_cox_str))[1:3], "-",sprintf("%.3f",coef(mod_cox_str))[4:7],NA,NA),
       "Exp(Coef_str)" = c(sprintf("%.3f",exp(coef(mod_cox_str)))[1:3], "-", sprintf("%.3f",exp(coef(mod_cox_str)))[4:7],NA,NA)) %>% 
  flextable() %>% 
  add_header_row(colwidth = c(1,2,2),
                 values = c("","時間との交互作用モデル","層化モデル")) %>% 
  flextable::align(align = "center", part = "all") %>% 
  set_caption("各モデルの推定値の比較")

表4.3: 各モデルの推定値の比較

	時間との交互作用モデル		層化モデル
Covariate	Coef(int)	Exp(Coef_int)	Coef(str)	Exp(Coef_str)
fin	-0.362	0.696	-0.359	0.698
age	0.085	1.089	-0.048	0.953
race	0.306	1.357	0.345	1.411
wexp	-1.209	0.298	-	-
mar	-0.234	0.791	-0.304	0.738
paro	-0.063	0.939	-0.063	0.939
prio	0.081	1.084	0.084	1.088
work	-1.318	0.268	-1.328	0.265
age:stop	-0.005	0.995
wexp:stop	0.041	1.042

4.4 観測期間の選択

今回の例では出所した日を観測の起点とするので比較的明確であるが、なかには観測時間の起点がそれほど明確でないデータもある。例えば、今回の再犯データでも個人の年齢や暦上の時間を観測時間の単位とすることも可能である。いずれにしても部分尤度法による推定は行えるが、重要な点はその観測時間の単位が妥当かを考えることである。例えばハザード率が強く年齢に依存しており、そのほかの時間単位にあまり依存していないと考えられるのであれば、年齢を観測時間の単位にすることは適切である。

理論的にはハザード率が二つ以上の時間に依存するモデルを定式化することはできるが、一般に大きなサンプルサイズや特殊な条件が必要である。このような方法が困難な場合は、異なる時間の単位を明示的に独立変数に含めるのが妥当である。今回も年齢(age)を独立変数に含めた。

4.5 コックス・モデルによる予測

第3章で見たように、予測という観点で見るとパラメトリックなモデルが最も優れており、予測が非常に簡単である。一方で、コックス回帰モデルでも限定的であるが予測を行うことはできる。

コックス回帰を用いて主に予測できるのは生存関数(= 時間の経過とともに事象が生じていない確率がどのように変化するかを表す関数)であり、実際に観察された時間の範囲について行える。詳しい推定方法は 杉本 (2021) などにあるが、モデル式の\(a(t)\)の部分(通常はそれを対数変換した基準ハザード関数)をノンパラメトリックな方法を用いて推定することが多いようだ。Rで基準ハザード関数がどのように推定されているかについては、こちらのサイトを参照。

生存関数には独立変数の値を指定することができ、これは実際に観測された値でなくても問題ない。例えば、1つ目のモデル(mod_cox)で、経済的支援を受けており、出所時の年齢21歳、黒人で未婚、仮釈放として出所し、就業経験があり、過去に有罪判決を4回受けている人について予測される生存確率は以下のようになる。

survfit(mod_cox, 
        newdata = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = 4),
        ## 信頼区間の範囲
        conf.int = 0.95) %>% 
  summary(times = c(seq(0,50,5),52)) 

## Call: survfit(formula = mod_cox, newdata = tibble(fin = 1, age = 21, 
##     race = 1, wexp = 1, mar = 0, paro = 1, prio = 4), conf.int = 0.95)
## 
##  time n.risk n.event survival std.err lower 95% CI upper 95% CI
##     0    432       0    1.000  0.0000        1.000        1.000
##     5    428       5    0.989  0.0053        0.979        1.000
##    10    418      10    0.967  0.0105        0.947        0.988
##    15    409      10    0.945  0.0151        0.916        0.975
##    20    397      15    0.911  0.0216        0.869        0.954
##    25    384      11    0.886  0.0262        0.836        0.939
##    30    374       9    0.865  0.0298        0.809        0.925
##    35    365      11    0.839  0.0341        0.775        0.909
##    40    351      14    0.806  0.0394        0.732        0.887
##    45    339      10    0.782  0.0430        0.702        0.871
##    50    325      15    0.746  0.0482        0.658        0.847
##    52    322       4    0.737  0.0495        0.646        0.840

作図にはsurveminerパッケージのggsurvplot()関数とggsurvfitパッケージのggsurvfit()関数が有用である。結果をggplotオブジェクトとして出力してくれるので、グラフの修飾が容易である。作り方の詳細はパッケージのウェブページを参考にされたし。上記と同じ条件で予測した生存関数を図示したものが図4.5である。なお、塗りつぶし部分は95%信頼区間である。

predict_cox <- survfit(mod_cox, 
        newdata = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = 4),
        ## 信頼区間の範囲
        conf.int = 0.95)

## ggsurvplot
ggsurvplot(predict_cox,
           data = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = 4),
           ## 色
           palette = "black",
           ## 塗りつぶしの濃さ
           conf.int.alpha = 0.15,
           size = 0.5,
           ## TRUEなら打ち切りデータの場所が明示される
           censor = FALSE, 
           ggtheme = theme_bw()) -> p1

p1$plot + 
 labs(x = "week", y = "survival probability")+
  ggtitle("ggsurvplot()")+
  theme_bw(base_size = 16)+
  theme(legend.position = "none")+
  coord_cartesian(ylim = c(0.64556,1))+
  scale_y_continuous(breaks = seq(0.65,1,0.05)) -> p1

## ggsurvfit
ggsurvfit(predict_cox)+
  add_confidence_interval()+
  labs(x = "week", y = "survival probability")+
  ggtitle("ggsurfit()")+
  theme_bw(base_size = 16)+
  scale_y_continuous(breaks = seq(0,1,0.05))　-> p2

p1 + p2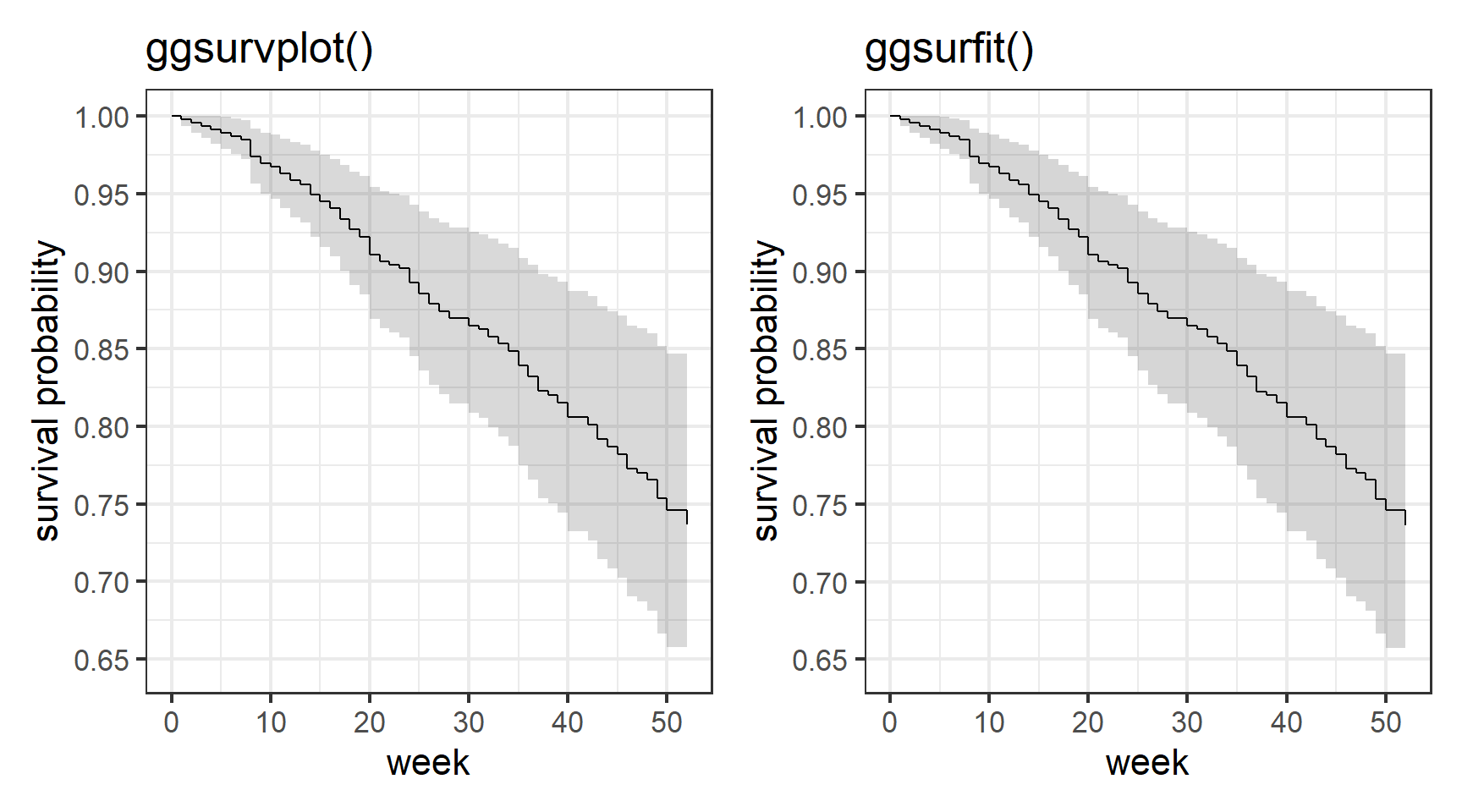

図4.5: モデルから推定された生存曲線

なお、何も指定しない場合、survfit()関数は連続変数は平均値で、二値変数は0で中心化した値を当てはめて予測を行う(図4.6)。

mod_cox$means

##       fin       age      race      wexp       mar      paro      prio 
##  0.000000 24.597222  0.000000  0.000000  0.000000  0.000000  2.983796

predict_cox2 <- survfit(mod_cox, 
        ## 信頼区間の範囲
        conf.int = 0.95)

## ggsurvplot
ggsurvplot(predict_cox2,
           data = recid,
           ## 色
           palette = "black",
           ## 塗りつぶしの濃さ
           conf.int.alpha = 0.15,
           size = 0.5,
           ## TRUEなら打ち切りデータの場所が明示される
           censor = FALSE, 
           ggtheme = theme_bw()) -> p3

p3$plot + 
 labs(x = "week", y = "survival probability")+
  theme_bw(base_size = 16)+
  theme(legend.position = "none")+
  coord_cartesian(ylim = c(0.64556,1))+
  scale_y_continuous(breaks = seq(0.65,1,0.05))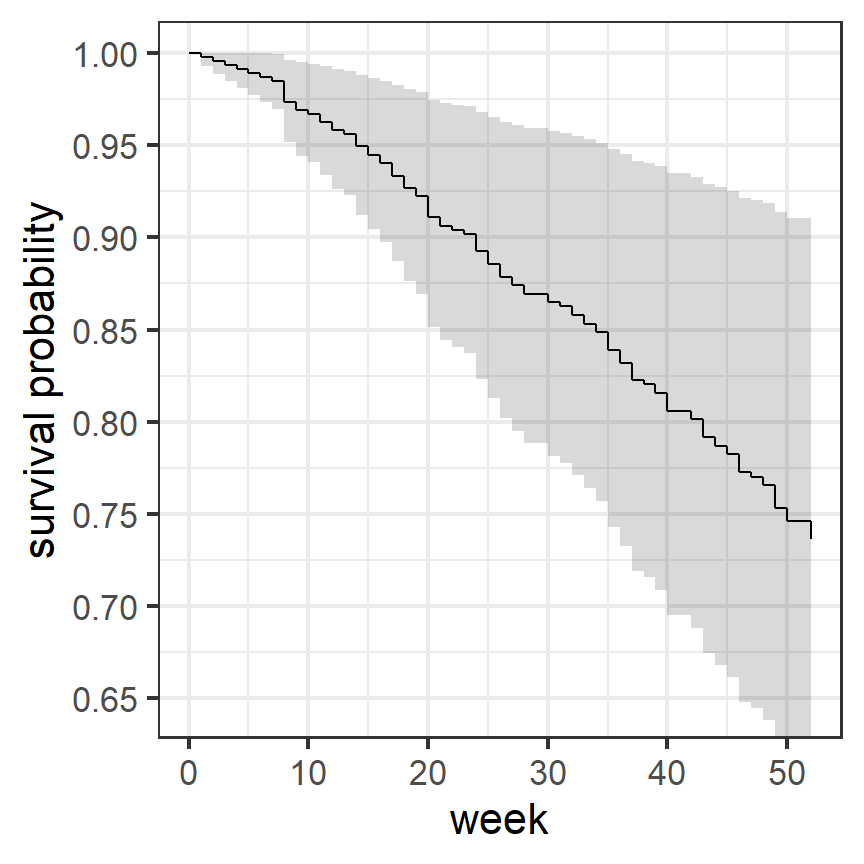 

図4.6: 独立変数を指定しないときにモデルから推定された生存曲線

複数の値を当てはめて生存関数を予測することもできる(図4.7)。ここでは、前科の数prioが0,5,10回のときの予測を行う。

predict_cox3 <- survfit(mod_cox, 
                        newdata = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = c(0,5,10)),
                        ## 信頼区間の範囲
                        conf.int = 0.95)

## ggsurvplot
ggsurvplot(predict_cox3,
           data = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = c(0,5,10)),
           ## 塗りつぶしの濃さ
           conf.int.alpha = 0.15,
           size = 0.5,
           ## TRUEなら打ち切りデータの場所が明示される
           censor = FALSE, 
           legend.title = "prio",
           legend.labs = c("0","5","10"),
           ggtheme = theme_bw()) -> p4

p4$plot + 
  scale_color_nejm()+
  scale_fill_nejm()+
  labs(x = "week", y = "survival probability")+
  theme_bw(base_size = 16)+
  theme(legend.position = "top")+
  coord_cartesian(ylim = c(0.4,1))+
  scale_y_continuous(breaks = seq(0,1,0.2)) 

図4.7: 独立変数を指定しないときにモデルから推定された生存曲線

時間依存独立変数を持つ場合も同様に予測することができる(図4.8)。

predict_cox_ti <- survfit(mod_cox_ti,
                        newdata = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = 4, work = c(0,1)),
                        ## 信頼区間の範囲
                        conf.int = 0.95)

## ggsurvplot
ggsurvplot(predict_cox_ti,
           data = tibble(fin = 1, age = 21, race = 1, wexp = 1, mar = 0, paro = 1, prio = 4, work = c(0,1)),
           ## 塗りつぶしの濃さ
           conf.int.alpha = 0.15,
           size = 0.5,
           ## TRUEなら打ち切りデータの場所が明示される
           censor = FALSE, 
           legend.title = "work",
           legend.labs = c(0,1),
           ggtheme = theme_bw()) -> p5

p5$plot + 
  scale_color_nejm()+
  scale_fill_nejm()+
  labs(x = "week", y = "survival probability")+
  theme_bw(base_size = 16)+
  theme(legend.position = "top")+
  coord_cartesian(ylim = c(0.5,1))+
  scale_y_continuous(breaks = seq(0,1,0.05))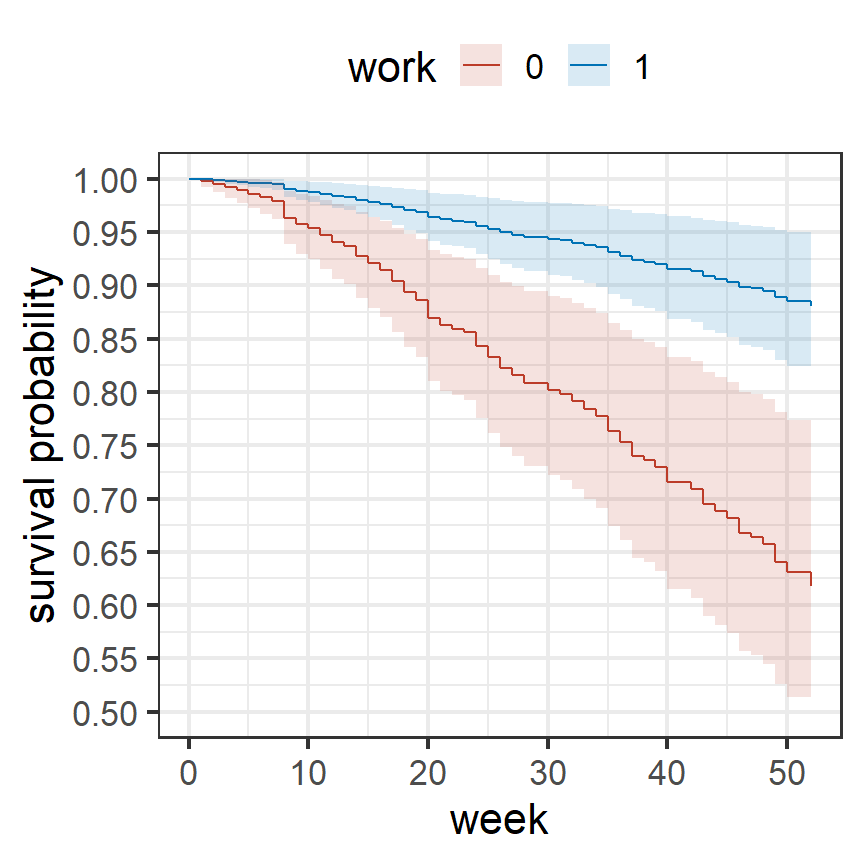 

図4.8: 時間依存独立変数をもつモデルから推定された生存曲線

References

Allison, P. D. (2014). Event history and survival analysis: Regression for longitudinal event data. SAGE Publications.

Cox, D. R. (1972). Regression models and life-tables. J. R. Stat. Soc., 34(2), 187–202.

杉本知之. (2021). 生存時間解析. 朝倉書店.

粕谷英一. (2012). 一般化線形モデル. 共立出版.

---

11. 比例ハザードモデルは\(h(t) = h_0(t) + exp(b_1x_1 + b_2x_2)\)のように表されることも多い。このとき、\(h_0(t)\)は基準ハザード関数(baseline hazard function)と呼ばれ、式(4.1)からわかるように\(h_0(t) = exp(a(t))\)である。↩︎

12. 交互作用の解釈については、 粕谷 (2012) なども参照。↩︎