2 パラメトリックな離散時間モデル

本章では、繰り返しのない単一の事象を離散時間モデルで分析するパラメトリックな方法を概観する。

2.1 離散時間モデルの例

ここでは具体例として、1950年代後半から60年代前半に博士号を取得した生化学者301人(助教として勤務経験あり)が准教授に昇進するのに要する年数を記録したデータを使用する。データはdataフォルダにある(rank.dta)。dta形式のファイルは、havenパッケージのread_dta()で読み込める。

library(haven)
rank <- read_dta("data/rank.dta")

データの先頭10行を取り出すと以下のようになっている。変数の説明は以下の通り。
ここでは、独立変数を用いて1年ごとの昇進の条件付き確率を回帰モデルを用いて推定することを目的とする。

従属変数にかかわる変数
- dur: 助教としての勤続年数
- promo: 助教への昇進の有無

独立変数(非時間依存変数)
- undgrad: 対象者の出身学部の選抜の厳しさの尺度
- phdprest: 博士号を取得した大学の威信の尺度
- phdmed: 医学博士の有無

独立変数(時間依存変数)
- prest: 勤務している大学の威信の尺度
- arts: 勤続年数ごとの累積発表論文数
- cits: 勤続年数ごとの論文の累積被引用回数

そのほか

  • jobtime: 職場を変わった場合、何年目に変わったか
rank %>% 
  datatable(options = list(scrollX = 100), rownames = FALSE)


准教授への昇進時期の分布は以下のようになる(表2.1)。なお、リスク集合(risk set)とは、各時点で事象を経験する可能性のある個体の集まり、ハザード率(hazard rate)とは、ある時点でリスク集合に入っている個体がその時点で事象を経験する条件付き確率である(i.e., この表では昇進人数/リスク集合の大きさ)。

打ち切りは、25人については10年たっても准教授に昇進できていないために生じているが、それ以外については大学を離れたために生じている。

rank %>% 
  group_by(dur) %>% 
  summarise(昇進人数 = sum(promo),
            打ち切り数 = sum(promo == "0")) %>% 
  rename(勤続年数 = dur) %>% 
  ungroup() -> hyou1

hyou1 %>% 
  mutate(勤続年数 = 勤続年数+1) %>% 
  mutate(N = 昇進人数 +　打ち切り数) %>% 
  mutate(sum = cumsum(N)) -> hyou1_b

hyou1 %>% 
  left_join(hyou1_b %>% select(勤続年数, sum)) %>% 
  replace_na(list(sum = 0)) %>% 
  mutate(リスク集合の大きさ = sum(昇進人数 + 打ち切り数) - sum) %>% 
  select(-sum) %>% 
  mutate(推定されたハザード率 = 昇進人数/リスク集合の大きさ) %>% 
  kable(align = "c", caption = "准教授への昇進時期の分布") %>% 
  kable_styling(font_size = 11, full_width = FALSE)
表2.1: 准教授への昇進時期の分布
勤続年数 昇進人数 打ち切り数 リスク集合の大きさ 推定されたハザード率
1 1 1 301 0.0033223
2 1 6 299 0.0033445
3 17 12 292 0.0582192
4 42 10 263 0.1596958
5 53 9 211 0.2511848
6 46 7 149 0.3087248
7 31 6 96 0.3229167
8 15 2 59 0.2542373
9 7 6 42 0.1666667
10 4 25 29 0.1379310

2.2 離散時間ハザード

イベント・ヒストリー分析では、上でも説明した「リスク集合」と「ハザード率」の二つが重要な概念である。分析ではハザード率を従属変数として、それぞれの独立変数がハザード率に与える影響を分析していく。

2.3 ロジスティック回帰モデル

離散時間モデルでは、ロジット変換3を利用することでハザード関数\(P(t)\)を以下のようにあらわす。なお、\(x_1\)は非時間依存変数を、\(x_2(t)\)は時間依存変数を表す。また、\(t\)は勤続年数を表す。\(b_1\)と\(b_2\)は偏回帰係数と呼ぶ。ロジット変換を施すことで、右辺がどのような値も取っても\(P(t)\)が0から1の範囲に収まる。

\[ \begin{equation} log\biggl(\frac{P(t)}{1-P(t)}\biggl) = b_0 + b_1x_1 + b_2x_2(t) + b_3t + b_4t^2 \tag{2.1} \end{equation} \]

2.4 モデルの推定

次に、データを基にパラメータ(\(b_1から b_4\))を推定する。推定は基本的に最尤法を用いて行う。これは、実際に観察された値が得られる確率が最大になるようにパラメータを推定する方法である。

実際の推定手順は以下のようになる。

  1. 各個体がリスク集合に入っている期間をある時間単位で分け(今回は1年)、その1単位ごと(= 人年ごと)に事象の発生を記録していく。
  2. 各個体は各単位ごとに(この場合は1年ごとに)昇進した場合は従属変数に1を、してない場合は0を割り当てられる。
  3. データセットを作成し、最尤法を用いてロジスティック回帰モデルのパラメータを推定する。

2.5 Rでの実装

2.5.1 データの加工

それでは、Rで実際にモデルのパラメータを推定してみる。分析をするためには、データフレームを縦長にする必要がある。具体的には、発表論文数(art1art10)と被引用数(cit1cit10)をそれぞれ一列にする必要がある。

rank %>% 
  ## 個体IDの列を作成
  rowid_to_column(var = "id") %>% 
  ## 勤続年数ごとの論文数を一列に
  pivot_longer(cols = art1:art10,
               names_to = "art",
               values_to = "art_n") %>% 
  ## 欠損値を除く
  filter(!is.na(art_n)) %>%
  arrange(id) %>% 
  ## 行番号を作る  
  rowid_to_column("rowid") %>% 
  select(-(cit1:cit10), -art) -> rank2

rank %>% 
  ## 個体IDの列を作成
  rowid_to_column(var = "id") %>% 
  ## 勤続年数ごとの引用数を一列に
  pivot_longer(cols = cit1:cit10,
               names_to = "cit",
               values_to = "cit_n") %>% 
  ## 欠損値を除く  
  filter(!is.na(cit_n)) %>%
  arrange(id) %>% 
  ## 行番号を作る  
  rowid_to_column("rowid") %>% 
  select(cit_n, rowid) -> rank3

## 結合
rank2 %>% 
  inner_join(rank3, by = "rowid") %>% 
  arrange(id) %>% 
  group_by(id) %>% 
  ## 個体ごとに勤続年数の列を作成
  mutate(year = row_number()) %>% 
  ## 変数promoが昇進のあった年のみ1をとるようにする  
  ungroup() %>% 
  mutate(promo = ifelse(year < dur,0,promo)) %>% 
  ## jobtimeの欠損値を0に
  replace_na(list(jobtime = 0)) %>% 
  ## 大学威信度の列を作成  
  mutate(jobpres = ifelse(year < jobtime, prest1, prest2)) %>% 
  select(-prest1, -prest2)-> rank4

できたデータシートは以下の通り。

datatable(rank4, options = list(scrollX = 100),
          rownames = FALSE)

2.5.2 分析

それでは、実際に分析する。分析には一般化線形モデルによる分析ができるglm()関数を用いる。

まずは1つ目のモデルとして、勤続年数を入れない線形モデルを考えてみる。

mod1 <- glm(promo ~ undgrad + phdmed + phdprest + jobpres + art_n + cit_n,
            data = rank4,
            family = binomial(link = "logit"))

結果は以下の通り(表2.2)。

model_parameters(mod1) %>% 
  data.frame() %>% 
  mutate(`95%CI` = str_c("[",sprintf("%.2f",CI_low),", ",sprintf("%.2f",CI_high),"}")) %>% 
  select(-df_error, -CI_low, -CI_high, -CI) %>% 
  select(Parameter, Coefficient, `95%CI`, everything()) %>% 
  kable(align = "c", caption = "mod1の結果") %>% 
  kable_styling(font_size = 11, full_width = FALSE)
表2.2: mod1の結果
Parameter Coefficient 95%CI SE z p
(Intercept) -2.9636747 [-3.80, -2.15} 0.4210727 -7.0383926 0.0000000
undgrad 0.1802769 [0.06, 0.30} 0.0607534 2.9673535 0.0030038
phdmed -0.2650547 [-0.58, 0.05} 0.1614778 -1.6414308 0.1007080
phdprest -0.0029980 [-0.18, 0.17} 0.0886335 -0.0338249 0.9730168
jobpres -0.2535299 [-0.46, -0.05} 0.1054517 -2.4042272 0.0162067
art_n 0.1270934 [0.10, 0.16} 0.0165769 7.6669053 0.0000000
cit_n -0.0014547 [-0.00, 0.00} 0.0012590 -1.1554230 0.2479173


2つ目のモデルとして、勤続年数とその二乗を説明変数に入れたモデルを考える。

mod2 <- glm(promo ~ undgrad + phdmed + phdprest + jobpres + art_n + cit_n + year + I(year^2),
            data = rank4,
            family = "binomial")

結果は以下の通り(表2.3)。

model_parameters(mod2) %>% 
  data.frame() %>% 
  mutate(`95%CI` = str_c("[",sprintf("%.2f",CI_low),", ",sprintf("%.2f",CI_high),"}")) %>% 
  select(-df_error, -CI_low, -CI_high, -CI) %>% 
  select(Parameter, Coefficient, `95%CI`, everything()) %>% 
  kable(align = "c", caption = "mod2の結果") %>% 
  kable_styling(font_size = 11, full_width = FALSE)
表2.3: mod2の結果
Parameter Coefficient 95%CI SE z p
(Intercept) -8.4846678 [-10.07, -7.02} 0.7756586 -10.9386630 0.0000000
undgrad 0.1939331 [0.07, 0.32} 0.0635127 3.0534551 0.0022622
phdmed -0.2356943 [-0.57, 0.10} 0.1717631 -1.3722061 0.1699993
phdprest 0.0270565 [-0.16, 0.21} 0.0931669 0.2904086 0.7715036
jobpres -0.2535406 [-0.48, -0.03} 0.1138113 -2.2277268 0.0258987
art_n 0.0733840 [0.04, 0.11} 0.0181374 4.0459977 0.0000521
cit_n 0.0001255 [-0.00, 0.00} 0.0013125 0.0956291 0.9238152
year 2.0818890 [1.65, 2.56} 0.2337665 8.9058484 0.0000000
I(year^2) -0.1585829 [-0.20, -0.12} 0.0203027 -7.8109434 0.0000000


2つのモデルを比較すると以下の通り。

stargazer(mod1, mod2, type = "text") 
## 
## ==============================================
##                       Dependent variable:     
##                   ----------------------------
##                              promo            
##                        (1)            (2)     
## ----------------------------------------------
## undgrad              0.180***      0.194***   
##                      (0.061)        (0.064)   
##                                               
## phdmed                -0.265        -0.236    
##                      (0.161)        (0.172)   
##                                               
## phdprest              -0.003         0.027    
##                      (0.089)        (0.093)   
##                                               
## jobpres              -0.254**      -0.254**   
##                      (0.105)        (0.114)   
##                                               
## art_n                0.127***      0.073***   
##                      (0.017)        (0.018)   
##                                               
## cit_n                 -0.001        0.0001    
##                      (0.001)        (0.001)   
##                                               
## year                               2.082***   
##                                     (0.234)   
##                                               
## I(year2)                           -0.159***  
##                                     (0.020)   
##                                               
## Constant            -2.964***      -8.485***  
##                      (0.421)        (0.776)   
##                                               
## ----------------------------------------------
## Observations          1,741          1,741    
## Log Likelihood       -595.566      -506.013   
## Akaike Inf. Crit.   1,205.132      1,030.025  
## ==============================================
## Note:              *p<0.1; **p<0.05; ***p<0.01

2.5.3 結果の解釈

モデル1(mod1)では(表2.2)、3つの独立変数が有意に准教授への昇進のハザード率に影響していることが分かる(undgrad、jobpres、art_n)。具体的には、より選抜度合いの高い大学を卒業した生化学者とより多くの論文を発表した生化学者はハザード率が高い。一方で、より威信度の高い大学で現在働いている生化学者ほどハザード率は低い。

各変数が1増加したときに、准教授に昇進するオッズ比(\(\frac{P(t)}{1-P(t)}\))がどの程度増加するかを計算すると(これは、\(e^{偏回帰係数}\)で求まる。式(2.1)を参照)、以下のようになる。すなわち、「学部選抜度(undgrad)」が1増えるとオッズ比が約1.2倍に、「累積論文発表数(art_n)」が1増えるとオッズ比が約1.14倍になる。一方、「勤務先の大学の威信度(jobpres)」が1増加すると、オッズ比は0.78倍に減少する。

model_parameters(mod1) %>% 
  data.frame() %>% 
  select(Parameter, Coefficient) %>% 
  mutate(odds = exp(Coefficient)) 
##     Parameter  Coefficient       odds
## 1 (Intercept) -2.963674661 0.05162885
## 2     undgrad  0.180276920 1.19754894
## 3      phdmed -0.265054700 0.76716399
## 4    phdprest -0.002998022 0.99700647
## 5     jobpres -0.253529874 0.77605656
## 6       art_n  0.127093447 1.13552312
## 7       cit_n -0.001454692 0.99854637

undgradとart_n、jobpresについて結果を図示すると以下のようになる(図2.1)。曲線はモデルに基づく回帰曲線を、塗りつぶし部分は95%信頼区間を表す。

fit_mod1_a <- ggpredict(mod1,
                      terms = c("art_n[0:50, by = 0.1]",
                                "undgrad[1:7,by = 3]"))

fit_mod1_a %>% 
  data.frame() %>% 
  rename(art_n = x, undgrad = group) %>% 
  ggplot(aes(x = art_n, y = predicted))+
  geom_line(aes(color = undgrad),
            linewidth = 1)+
  geom_ribbon(aes(fill = undgrad,
                  ymin = conf.low, ymax = conf.high),
              alpha = 0.2)+
  labs(y = "ハ\nザ\nǀ\nド\n率")+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1,
        legend.position = "none",
        axis.title.y = element_text(angle = 0, vjust = 0.5))+
  scale_color_nejm()+
  scale_fill_nejm() -> p_fit1_a

fit_mod1_b <- ggpredict(mod1,
                      terms = c("jobpres[0:5, by = 0.01]",
                                "undgrad[1:7,by = 3]"))
fit_mod1_b %>% 
  data.frame() %>% 
  rename(jobpres = x, undgrad = group) %>% 
  ggplot(aes(x = jobpres, y = predicted))+
  geom_line(aes(color = undgrad),
            linewidth = 1)+
  geom_ribbon(aes(fill = undgrad,
                  ymin = conf.low, ymax = conf.high),
              alpha = 0.2)+
  labs(y = "ハ\nザ\nǀ\nド\n率")+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1,
        axis.title.y = element_text(angle = 0, vjust = 0.5))+
  scale_color_nejm()+
  scale_fill_nejm() -> p_fit1_b

p_fit1_a + p_fit1_b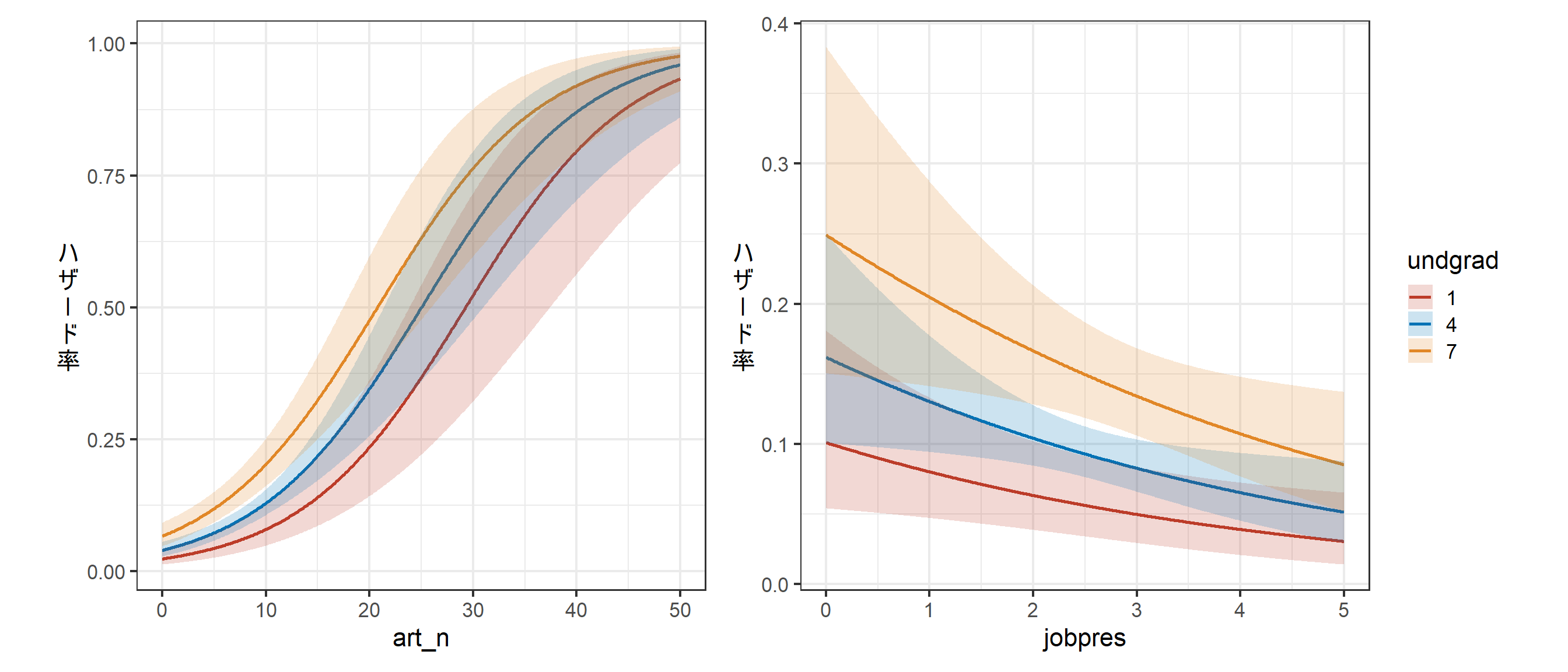
モデル1の推定結果

図2.1: モデル1の推定結果


モデル2も結果自体は大きく変わらないが、勤続年数とその二乗が有意に影響していることが分かる。また、「累積論文発表数(art_n)」の偏回帰係数が大幅に小さくなっており、オッズ比も1.14倍から1.08倍に減少している。

model_parameters(mod2) %>% 
  data.frame() %>% 
  select(Parameter, Coefficient) %>% 
  mutate(odds = exp(Coefficient))
##     Parameter   Coefficient        odds
## 1 (Intercept) -8.4846678008 0.000206612
## 2     undgrad  0.1939331150 1.214015081
## 3      phdmed -0.2356943107 0.790022138
## 4    phdprest  0.0270564703 1.027425820
## 5     jobpres -0.2535405982 0.776048238
## 6       art_n  0.0733840049 1.076143702
## 7       cit_n  0.0001255168 1.000125525
## 8        year  2.0818890246 8.019603843
## 9   I(year^2) -0.1585829127 0.853352207

undgradとart_n、jobpresについて結果を図示すると以下のようになる(図2.2)。左図の傾きが図2.1に比べて緩やかになっており、図からもモデル1との違いが読み取れる。

fit_mod2_a <- ggpredict(mod2,
                      terms = c("art_n[0:50, by = 0.1]",
                                "undgrad[1:7,by = 3]"))

fit_mod2_a %>% 
  data.frame() %>% 
  rename(art_n = x, undgrad = group) %>% 
  ggplot(aes(x = art_n, y = predicted))+
  geom_line(aes(color = undgrad),
            linewidth = 1)+
  geom_ribbon(aes(fill = undgrad,
                  ymin = conf.low, ymax = conf.high),
              alpha = 0.2)+
  labs(y = "ハ\nザ\nǀ\nド\n率")+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1,
        legend.position = "none",
        axis.title.y = element_text(angle = 0, vjust = 0.5))+
  scale_color_nejm()+
  scale_fill_nejm() -> p_fit2_a

fit_mod2_b <- ggpredict(mod2,
                      terms = c("jobpres[0:5, by = 0.01]",
                                "undgrad[1:7,by = 3]"))
fit_mod2_b %>% 
  data.frame() %>% 
  rename(jobpres = x, undgrad = group) %>% 
  ggplot(aes(x = jobpres, y = predicted))+
  geom_line(aes(color = undgrad),
            linewidth = 1)+
  geom_ribbon(aes(fill = undgrad,
                  ymin = conf.low, ymax = conf.high),
              alpha = 0.2)+
  labs(y = "ハ\nザ\nǀ\nド\n率")+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1,
        axis.title.y = element_text(angle = 0, vjust = 0.5))+
  scale_color_nejm()+
  scale_fill_nejm() -> p_fit2_b

p_fit2_a + p_fit2_b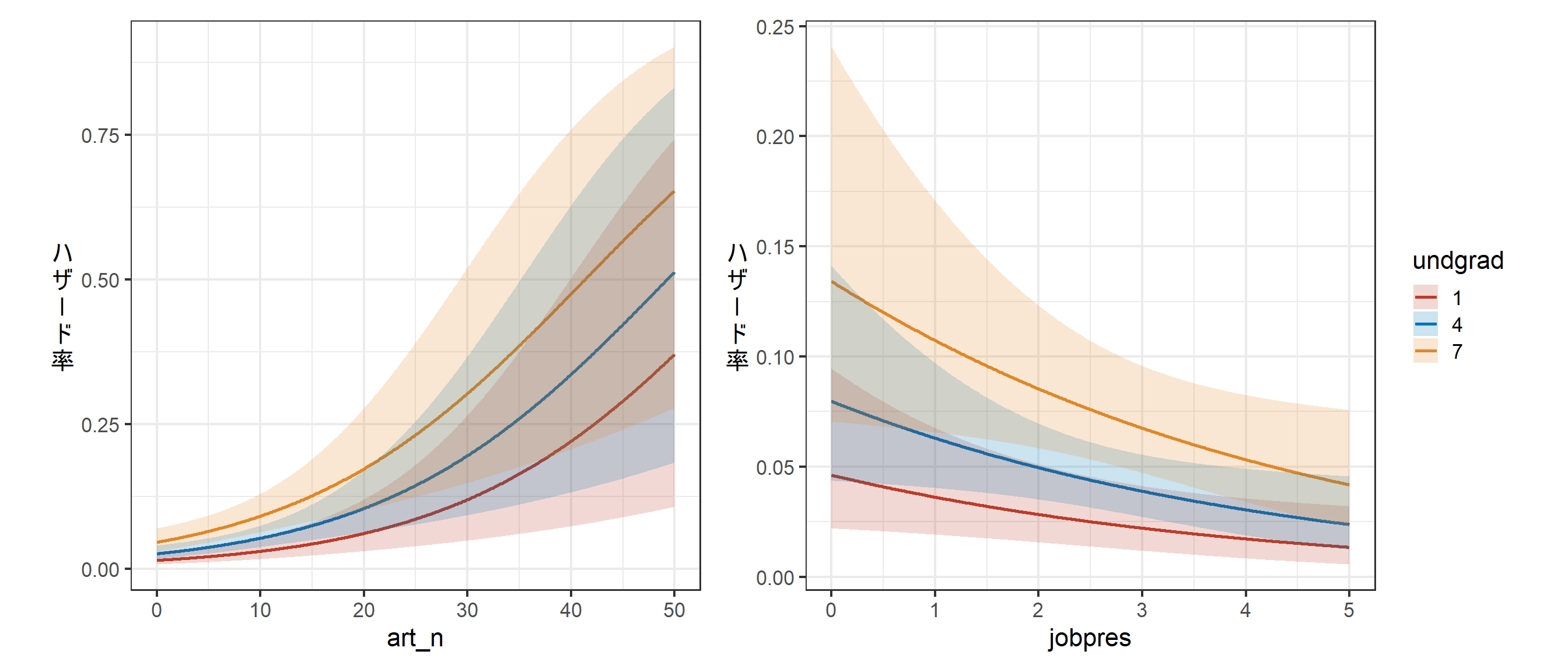
モデル2の推定結果

図2.2: モデル2の推定結果

2.6 尤度比検定

あるモデルが別のモデルの「入れ子」構造(一方のモデルが他方のモデルの独立変数をすべて含む)であるとき、尤度比検定によってどちらの方が適合度が高いか検定を行うことができる。2つのモデルの対数尤度の差の2倍が\(\chi^2\)分布に近似できることを利用して帰無仮説検定を行うことが多い4。

Rでは以下のように行う。結果を見ると、モデル2の方が有意に適合度が高いことが分かる。 このような検定は、本稿で以後出てくるモデルやパラメータの検定にも応用可能である。

anova(mod1,mod2, test = "Chisq")
## Analysis of Deviance Table
## 
## Model 1: promo ~ undgrad + phdmed + phdprest + jobpres + art_n + cit_n
## Model 2: promo ~ undgrad + phdmed + phdprest + jobpres + art_n + cit_n + 
##     year + I(year^2)
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1      1734     1191.1                          
## 2      1732     1012.0  2   179.11 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

2.7 離散時間ロジスティック回帰モデルの注意点

上記のモデルにはいくつか注意点がある。

  1. 一個体が複数の事象を経験する場合は、事象の回数の影響を修正する必要がある。
    ロバスト推定による標準誤差を求めたり、一般化推定式やランダム(変量)効果モデルを用いたりする。

  2. 区切る時間単位を適切に設定する必要がある。
    今回は、准教授の昇進が各年度の初めに行われるため、1年ごとにデータを区切ることは適切であった。これを1日ごとに区切るとデータが膨大になってしまうし、５年ごとに区切ると多くの情報が失われてしまう。分析対象の事象に応じて、適切に区切る時間単位を適切に設定する必要がある。

  3. 代替手法
    式(2.1)は独立変数のハザード率に対する影響を検討する最も知られた方法だが、以下の「補対数対数モデル」も代替手法として有用である。このモデルでも、右辺がどのような値をとろうと\(P(t)\)は0から1に収まる。

\[ \begin{equation} log[-log(1-P(t))] = b_0 + b_1x_1 + b_2x_2(t) + b_3t + b_4t^2 \tag{2.2} \end{equation} \]

Rでは、以下のように実装できる。

mod3 <- glm(promo ~ undgrad + phdmed + phdprest + jobpres + art_n + cit_n + year + I(year^2),
            data = rank4,
            family = binomial(link = "cloglog"))

結果は以下の通り(表2.4)。ロジスティック回帰モデルと結果は大きく変わらない。特にP値だけに着目する場合はどちらのモデルを選んでも決定的な差はない。

model_parameters(mod3) %>% 
  data.frame() %>% 
  mutate(`95%CI` = str_c("[",sprintf("%.2f",CI_low),", ",sprintf("%.2f",CI_high),"}")) %>% 
  select(-df_error, -CI_low, -CI_high, -CI) %>% 
  select(Parameter, Coefficient, `95%CI`, everything()) %>% 
  kable(align = "c", caption = "mod3の結果") %>% 
  kable_styling(font_size = 11, full_width = FALSE)
表2.4: mod3の結果
Parameter Coefficient 95%CI SE z p
(Intercept) -7.9961202 [-9.40, -6.69} 0.6943534 -11.5159220 0.0000000
undgrad 0.1694896 [0.06, 0.28} 0.0548959 3.0874751 0.0020186
phdmed -0.2153786 [-0.50, 0.08} 0.1469985 -1.4651751 0.1428732
phdprest 0.0100102 [-0.15, 0.17} 0.0806278 0.1241530 0.9011941
jobpres -0.1934044 [-0.38, -0.01} 0.0967829 -1.9983313 0.0456808
art_n 0.0623539 [0.03, 0.09} 0.0142864 4.3645723 0.0000127
cit_n -0.0004238 [-0.00, 0.00} 0.0010398 -0.4075788 0.6835830
year 1.9223437 [1.53, 2.36} 0.2128381 9.0319539 0.0000000
I(year^2) -0.1469834 [-0.19, -0.11} 0.0184860 -7.9510496 0.0000000


undgradとart_n、jobpresについて結果を図示すると以下のようになる(図2.3)。

fit_mod3_a <- ggpredict(mod3,
                      terms = c("art_n[0:50, by = 0.1]",
                                "undgrad[1:7,by = 3]"))

fit_mod3_a %>% 
  data.frame() %>% 
  rename(art_n = x, undgrad = group) %>% 
  ggplot(aes(x = art_n, y = predicted))+
  geom_line(aes(color = undgrad),
            linewidth = 1)+
  geom_ribbon(aes(fill = undgrad,
                  ymin = conf.low, ymax = conf.high),
              alpha = 0.2)+
  labs(y = "ハ\nザ\nǀ\nド\n率")+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1,
        legend.position = "none",
        axis.title.y = element_text(angle = 0, vjust = 0.5))+
  scale_color_nejm()+
  scale_fill_nejm() -> p_fit3_a

fit_mod3_b <- ggpredict(mod3,
                      terms = c("jobpres[0:5, by = 0.01]",
                                "undgrad[1:7,by = 3]"))
fit_mod3_b %>% 
  data.frame() %>% 
  rename(jobpres = x, undgrad = group) %>% 
  ggplot(aes(x = jobpres, y = predicted))+
  geom_line(aes(color = undgrad),
            linewidth = 1)+
  geom_ribbon(aes(fill = undgrad,
                  ymin = conf.low, ymax = conf.high),
              alpha = 0.2)+
  labs(y = "ハ\nザ\nǀ\nド\n率")+
  theme_bw(base_size = 16)+
  theme(aspect.ratio = 1,
        axis.title.y = element_text(angle = 0, vjust = 0.5))+
  scale_color_nejm()+
  scale_fill_nejm() -> p_fit3_b

p_fit3_a + p_fit3_b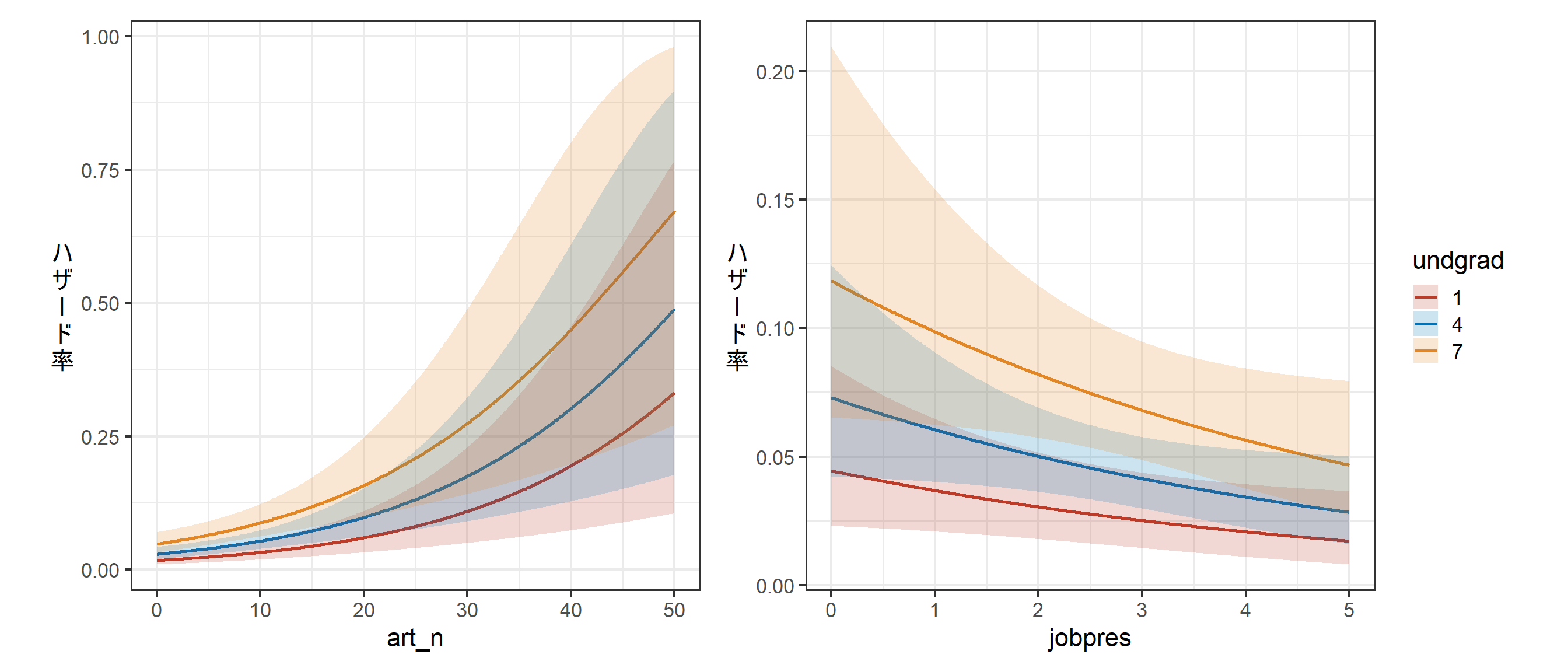
モデル3の推定結果

図2.3: モデル3の推定結果

2.8 打ち切りデータの扱い

今回のデータでは打ち切りは以下の2通りで生じており、これらは「右側打ち切り(right censoring)」と呼ばれ、最後に対象が観察された時点で事象がまだ発生していないことによるものである。

  1. 10年経ってもまだ准教授に昇進していない(= 固定打ち切り(fixed censoring)))
    打ち切りの時点は全ての個体で同じ。

  2. 准教授昇進前に大学を辞めた(= ランダムな打ち切り(random censoring))
    打ち切りの時点は個体によって異なる。脂肪や転居による追跡の終了などが理由。ただし、「ランダム」とは打ち切りのタイミングが変数と一切関係ないという意味でない点に注意。

2の場合、ほぼすべてのイベント・ヒストリー分析では打ち切りが生じた時間は「無情報」であると仮定している。すなわち、特定の時点である個体に打ち切りが生じても、その個体のハザード率には何の要因も影響していないことを仮定している。この仮定は、今回の例では昇進の可能性の低い研究者ほど大学を辞める傾向があるのであれば妥当ではない。おそらく何人かは准教授に昇進できずに雇用期間が終了したことが打ち切りの原因になっていたと考えられる。　　

しかし、今のところこの仮定を緩めて分析する方法はなく、ほとんどの研究者はこの問題に目をつぶって分析を行うしかない。そのため、研究デザインの段階でランダムでない打ち切りを最小限にするために可能な限りあらゆることを行う必要がある。

2.9 離散時間モデルと連続時間モデル

一般的に、離散時間モデルは後述する連続時間モデルと極めて似た結果をもたらすことが多い。実際、式(2.1)の離散時間モデルは、時間の単位を小さくするにつれて第4章で見る比例ハザードモデルに近づく。したがって、離散時間モデルと連続時間モデルのいずれを用いるかは一般的に計算にかかる手間と簡便さを考慮して判断する。時間依存の独立変数がない場合、しばしば以降の2つの章で説明する連続時間モデルを使う方が簡単である。他方、時間依存の独立変数があるならば、いずれのモデルでも手間や簡便さは変わらない。

References

久保拓弥. (2012). データ解析のための統計モデリング入門. 岩波書店.
粕谷英一. (2012). 一般化線形モデル. 共立出版.

  1. ロジット変換がわからない方はこちら。　　↩︎

  2. 対数尤度や尤度比検定の詳細については、 粕谷 (2012) や 久保 (2012) を参照。パラメトリックブーストラップ法を用いたより正確な検定を行うこともできる(久保, 2012)。↩︎