2 確率分布の基礎
2.1 確率分布とは
前章(1)において、統計モデルでは「データに確率モデルを当てはめて、現象の解釈や予測をおこなう」と書きました。確率モデルの記述に必要になってくるのが確率分布です。確率分布は、確率変数とそれが得られる確率との対応を表したものです。確率変数とは、確率的な法則に従って値がランダムに変化する値のことを表します。統計学では、データが確率的な過程によって得られると仮定するので、データは確率変数です。
- 確率変数: 確率的な法則に従って値がランダムに変化する値(e.g., データ)
- 確率分布: 確率変数とそれが得られる確率との対応を表したもの
2.2 確率分布とパラメータ
確率分布はパラメータ(母数)によって形が決まります。後述しますが、例えば正規分布はその期待値(=平均)\(\mu\)と分散\(\sigma^2\)によって形が決まります(図2.1)。統計モデルでは、データから確率分布のパラメータを推定することになります。
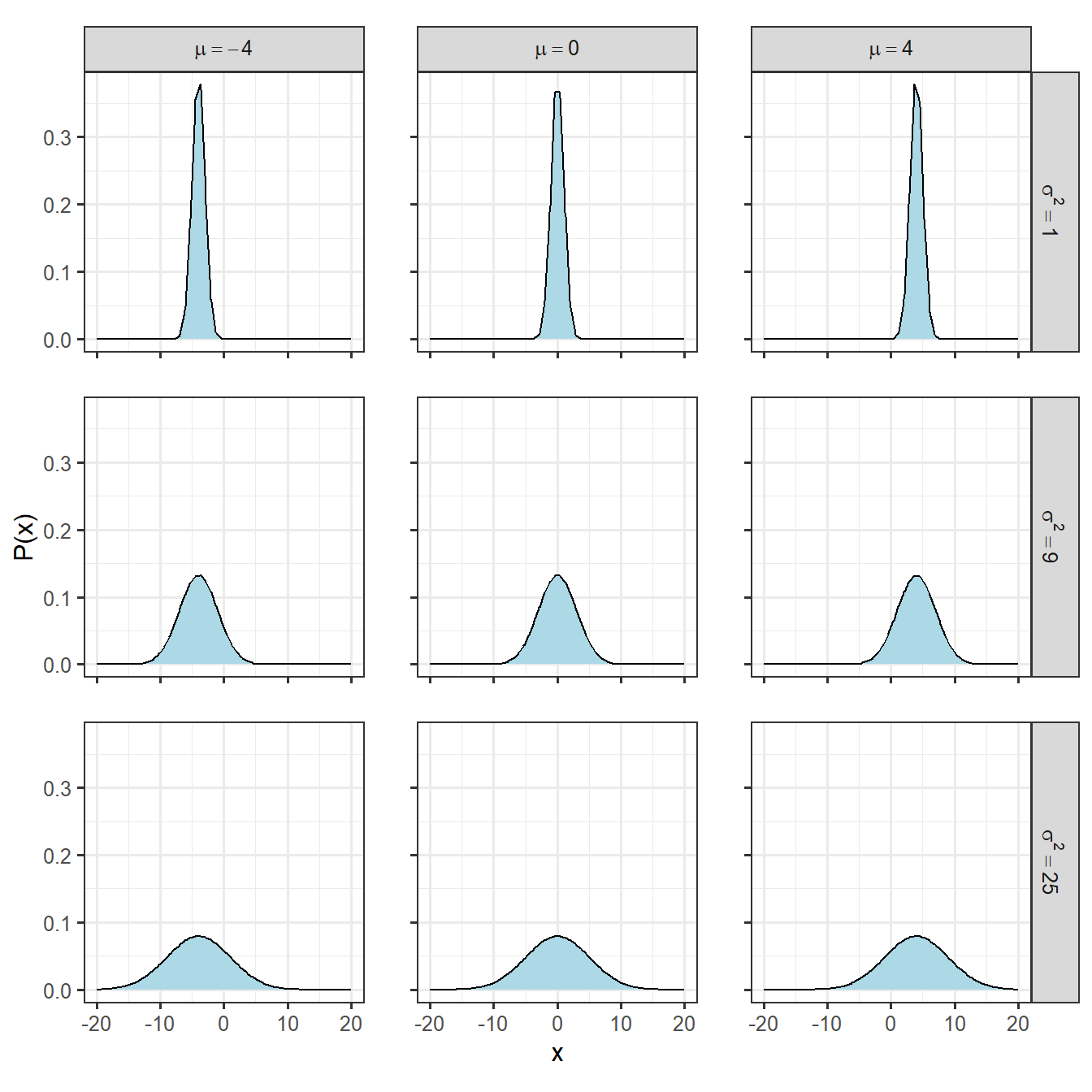
図2.1: 様々な正規分布
2.3 連続変数と離散変数
確率変数には連続型なものと離散型なものがあります。連続型の変数は、雑に言ってしまえば小数点以下をとることができ、計測を精密にすればするほどより細かい値が得られるものを指します(e.g., 体重、気温)。一方で離散型の変数は、\(1,2,3,\dots\)のように小数点以下の値をとりえない量的な変数(e.g., 発生回数など)や質的な変数(e.g., オス/メス、大/中/小)のことを指します。
- 連続型: 小数点以下をとることができる量的な変数(e.g., 体重、気温)
- 離散型: 小数点以下の値をとりえない量的な変数/質的変数(e.g., 発生回数、大/中/小)
確率分布は連続的か離散的かなど、確率変数がどのようなものかによって変わります。以下では、実際にどのような確率分布があるか見ていきましょう。
2.4 連続型の確率分布
連続型の量的データを対象とする際には、連続型の確率分布を用います。確率分布は、確率密度関数によって表されます。確率密度関数を\(f(x)\)とするとき、確率変数がa以上b以下の値をとる確率は以下のように表されます。確率密度関数は複雑な数式で表されますが、覚える必要はありません。
\[ \int_a^b f(x) dx \]
それでは、実際に連続型の確率分布の例を見ていきましょう。
2.4.1 正規分布
正規分布はガウス分布とも呼ばれ、平均値に対して左右対称な釣り鐘型になります。正規分布は先ほど触れたように期待値\(\mu\)と分散\(\sigma^2\)という2つのパラメータによって形が決まり、確率密度関数は以下のようになります。
- 期待値: \(\mu\)
- 分散: \(\sigma^2\)
\[ P(x) = \frac{1}{\sqrt{2 \pi \sigma^2}}exp(-\frac{(x-\mu)^2}{2\sigma^2}) \]
\(\mu\)と\(\sigma^2\)の値を変えたときの分布の形は図2.1に示した通りです。
2.4.2 コーシー分布
コーシー分布も左右対称な釣り鐘型になりますが、正規分布よりが裾の長いという特徴を持ちます。\(\mu\)と\(\sigma\)という2つのパラメータによって形が決まり、確率密度関数は以下のようになります。なお、コーシー分布は期待値と分散が存在しない特殊な分布です。
\[ P(x) = \frac{1}{\pi\sigma} \frac{1}{1 + ((x - \mu)/\sigma)^2} \]
\(\mu\)と\(\sigma\)の値を変えたときの分布の形は図2.2の通りです。正規分布よりも裾が長いことが分かります。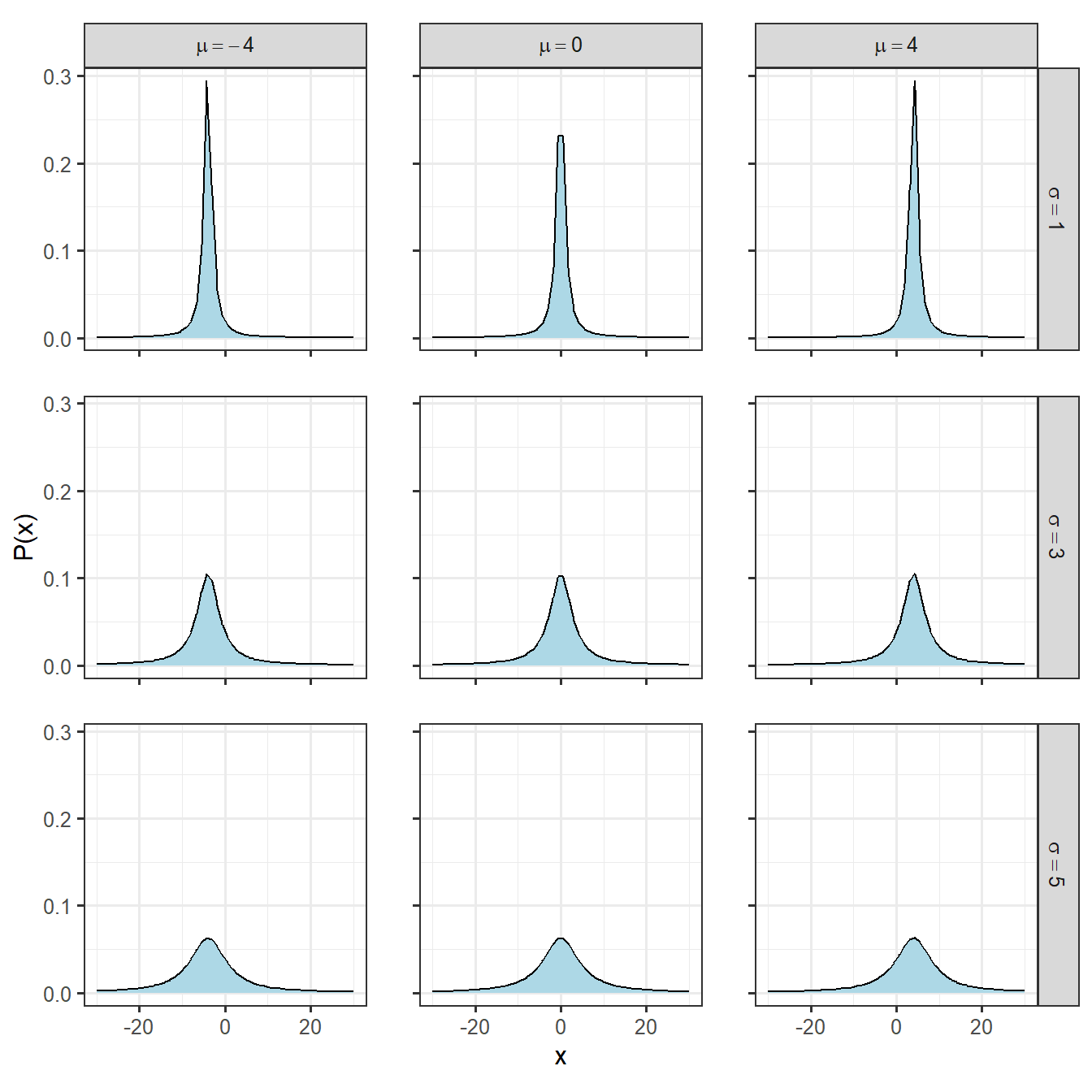
図2.2: 様々なコーシー分布
2.4.3 Studentのt分布
Studentのt分布も前出の2つと同様に左右対称な釣り鐘型になります。\(\mu\)、\(\sigma\)、\(\nu\)(自由度)という3つのパラメータがあり、確率密度関数は以下のようになります。なお、\(\Gamma()\)はガンマ関数を表します。自由度\(\nu\)の値によって分布の裾の長さが決まり、\(\nu = 1\)のときはコーシー分布と、\(\nu = \infty\)のときは正規分布と一致します。つまり、自由度が大きいほど裾の狭い分布になります。
\[ P(x) = \frac{\Gamma((\nu + 1)/2)}{\Gamma(\nu/2)\sqrt{pi\nu\sigma}} \Bigl(1 + \frac{1}{\nu} \bigl(\frac{x - \mu}{\sigma} \bigl)^2 \Bigl)^{-(x+1)/2} \]
分布の期待値と分散は以下のようになります。
- 期待値:\(\nu > 1\)ならば\(\mu\)、それ以外は存在しない
- 分散: \(\nu > 2\)ならば\(\sigma^2\nu/(\nu-2)\)、\(1 < \nu \le 2\)の場合は\(\infty\)、それ以外は存在しない
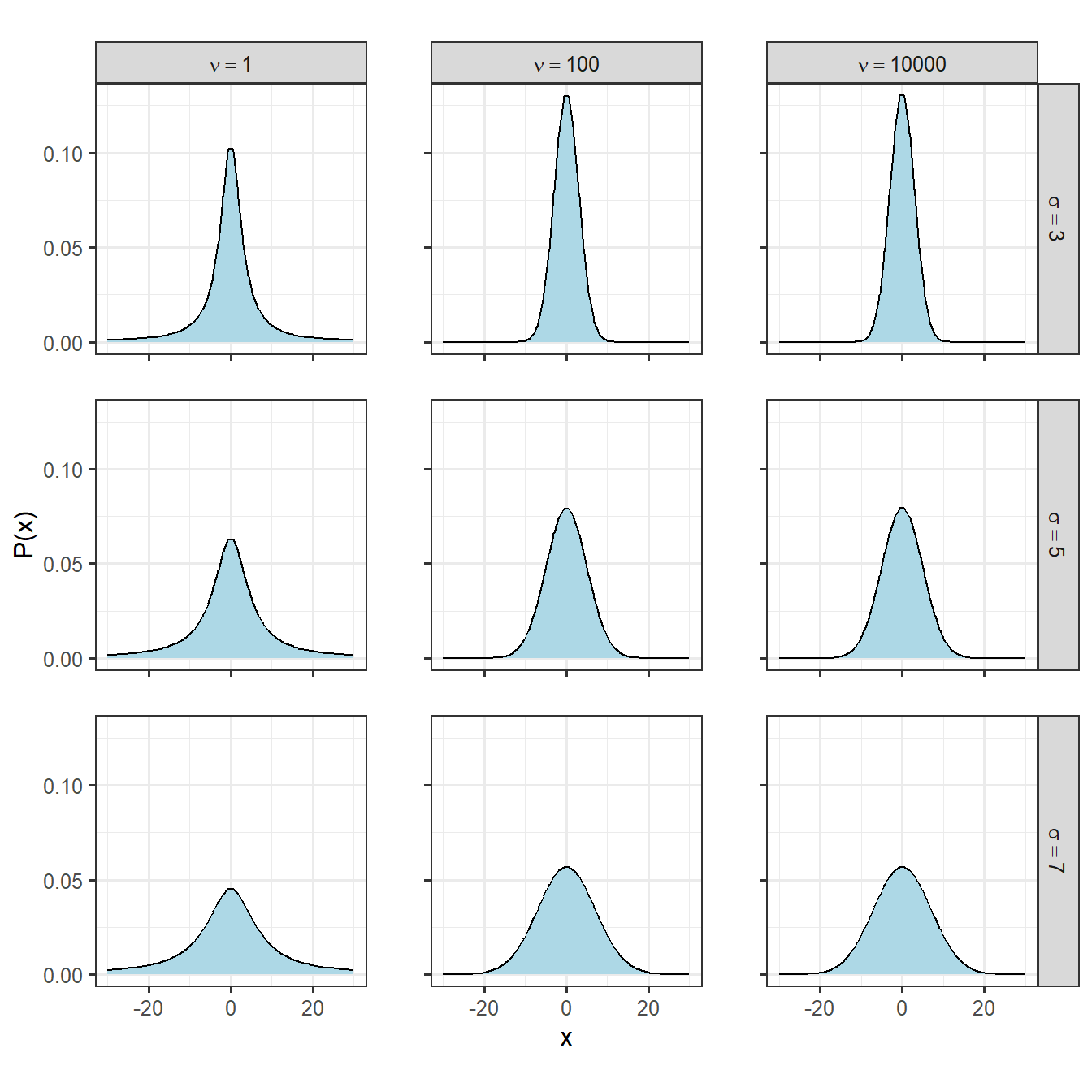
図2.3: 様々なStudentのt分布
2.4.4 ガンマ分布
ガンマ分布は正の値のみをとる連続型の量的データに用いられる分布です。\(\alpha\)と\(\beta\)という2つのパラメータをとり、確率密度関数は以下のようになります。\(\alpha\)は形状(shape)パラメータ、\(\beta\)はrateパラメータと呼ばれます。
\[ P(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1} exp(-\beta x) \]
分布の期待値と分散は以下のようになります。
- 期待値: \(\alpha/\beta\)
- 分散: \(\alpha/\beta^2\)
パラメータを変化させたときの分布の変化は以下の通りです(図2.4)。
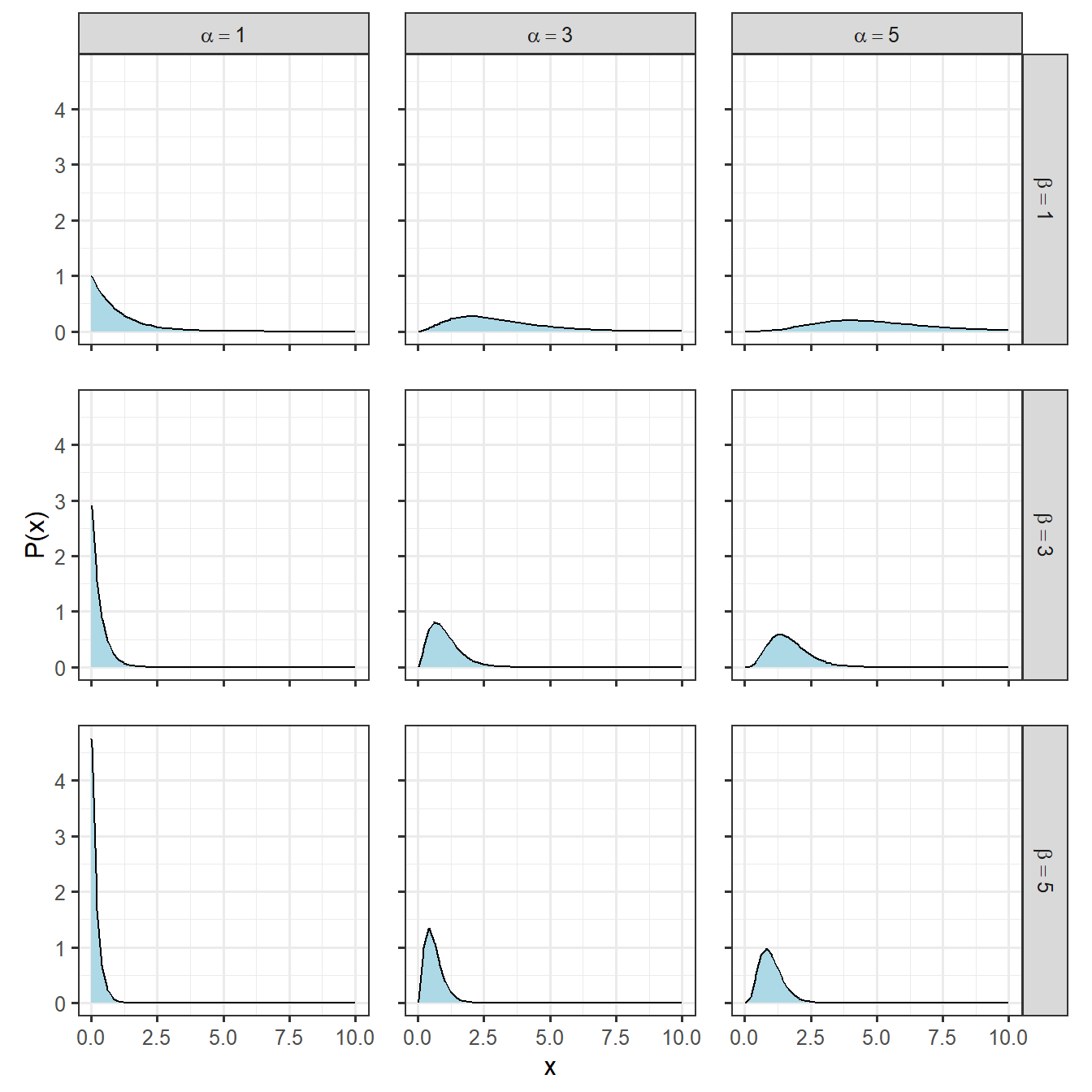
図2.4: 様々なガンマ分布
2.4.5 ベータ分布
ベータ分布は0から1までの値のみをとる連続型の量的データに用いられる分布です。パラメータ\(\alpha\)と\(\beta\)を用いて表され、確率密度関数は以下の通りになります。なお、\(B()\)はベータ関数です。
\[ P(x) = \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha, \beta)} \]
期待値\(\bar{p}\)とshape parameterの\(\theta\)の2つのパラメータで定義され、確率密度関数は以下のようになります。なお、\(\theta = \alpha + \beta\)は分布の広さを表し、\(\theta\)が2より大きくなると分布は狭くなり、\(\theta\)が2以下になると0と1に分布が集中していきます。\(\theta\)が2のときは一様分布です。
ベータ分布の期待値と分散は以下のようになります。
- 期待値: \(\frac{\alpha}{\alpha + \beta}\)
- 分散: \(\frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}\)
様々なベータ分布を書いてみると以下のようになります(図2.5)。
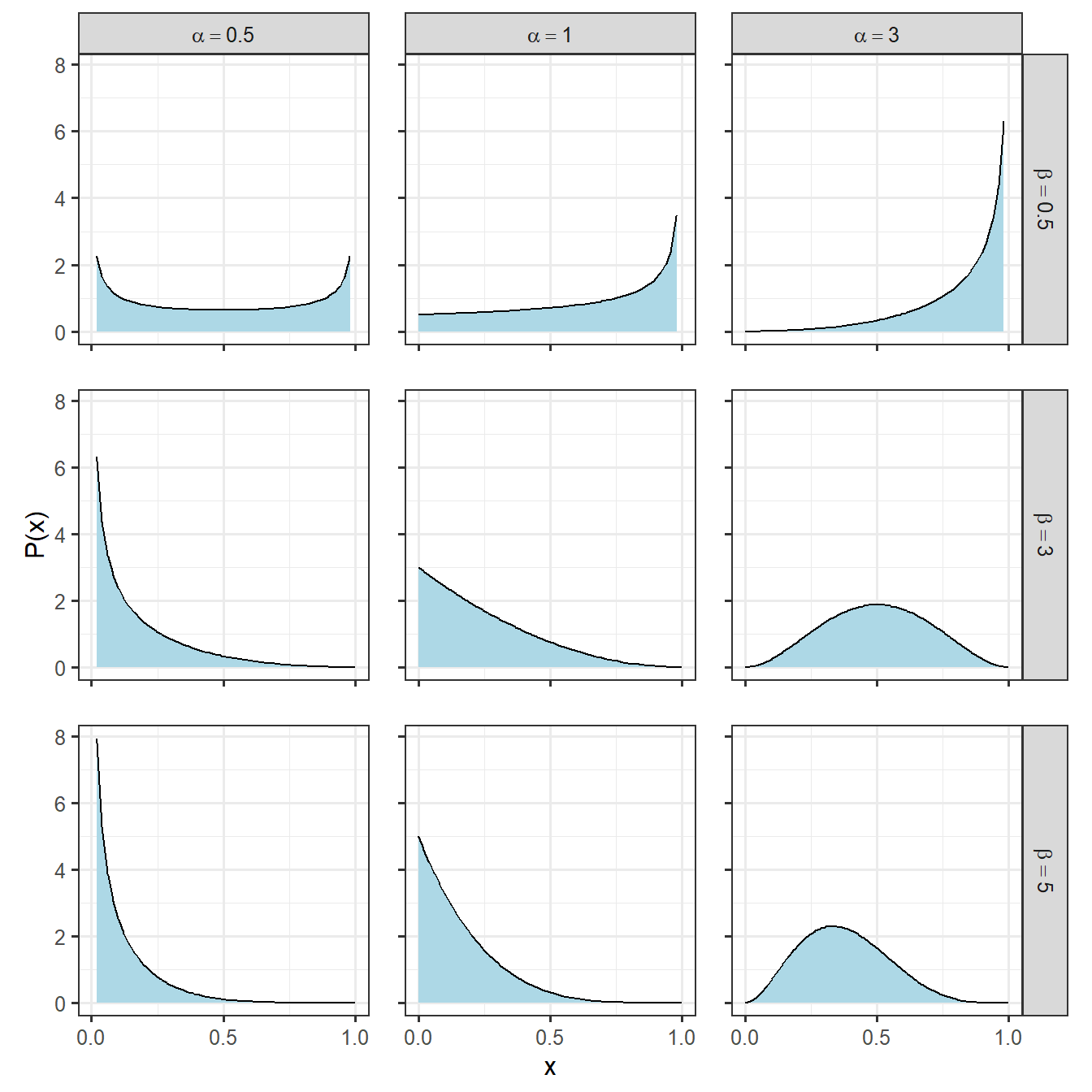
図2.5: 様々なベータ分布
2.5 離散型の確率分布
離散型のデータを対象とする際には、離散型の確率分布を用います。離散型の確率分布は、確率質量関数によって表されます。確率質量関数を\(f(x)\)とするとき、確率変数がa以上b以下の値をとる確率は以下のように表されます。確率質量関数も覚える必要はありません。
\[ \Sigma_{i = a}^bf(x_i) \]
それでは、実際に連続型の確率分布の例を見ていきましょう。
2.5.1 ベルヌーイ分布
ベルヌーイ分布は0/1、成功/失敗のように2つの結果しか持たない変数を対象とするときに用います。便宜上、一方の結果が得られる確率を成功確率(\(p\))と呼びます。成功を1、失敗を0とするとき、確率質量関数は以下のようになります。パラメータは成功確率\(p\)のみです。
\[ \begin{aligned} &P(x = 1) = p\\ &P(x = 0) = 1-p \end{aligned} \]
分布の期待値と分散は以下のようになります。
- 期待値: \(p\)
- 分散: \(p(1-p)\)
様々なベルヌーイ分布を書いてみると以下のようになります(図2.6)。
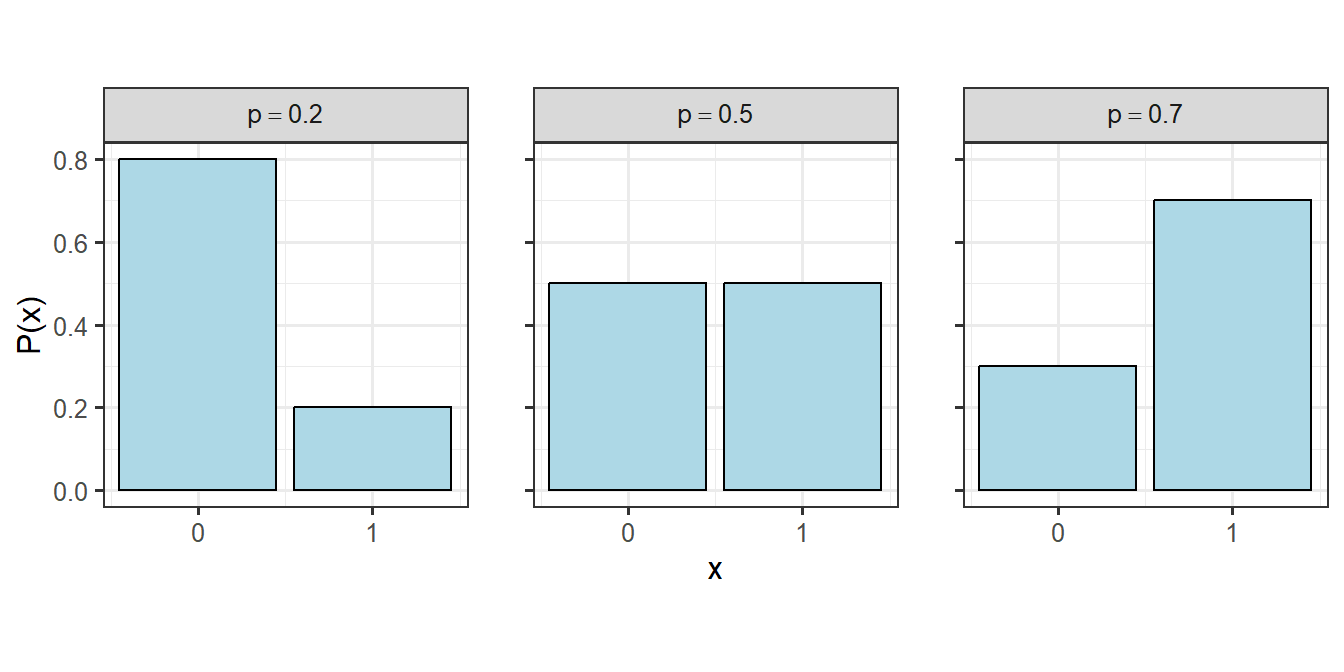
図2.6: 様々なベルヌーイ分布
2.5.2 二項分布
二項分布は、「結果が2通り(例えば、成功/失敗)である試行(ベルヌーイ試行)を独立に\(n\)回行ったときの成功回数の分布を表した確率分布」です。つまり、上限のある整数値をとる変数や整数を用いた割合を表す変数に対して用いることができます。例えば、 コインを10回振ったときに表が出る回数は二項分布に従います。
ベルヌーイ試行の成功確率を\(p\)とするとき、\(n\)回中\(x\)回成功する確率\(p(x)\)は以下のように書けます。これが二項分布の確率質量関数です。
\[ P(x) = _n C _x p^x(1-p)^{n-x} \quad (x \geq 0) \]
分布の期待値と分散は以下のようになります。
- 期待値: \(np\)
- 分散: \(np(1-p)\)
様々な二項分布を書いてみると以下のようになります(図2.7)。
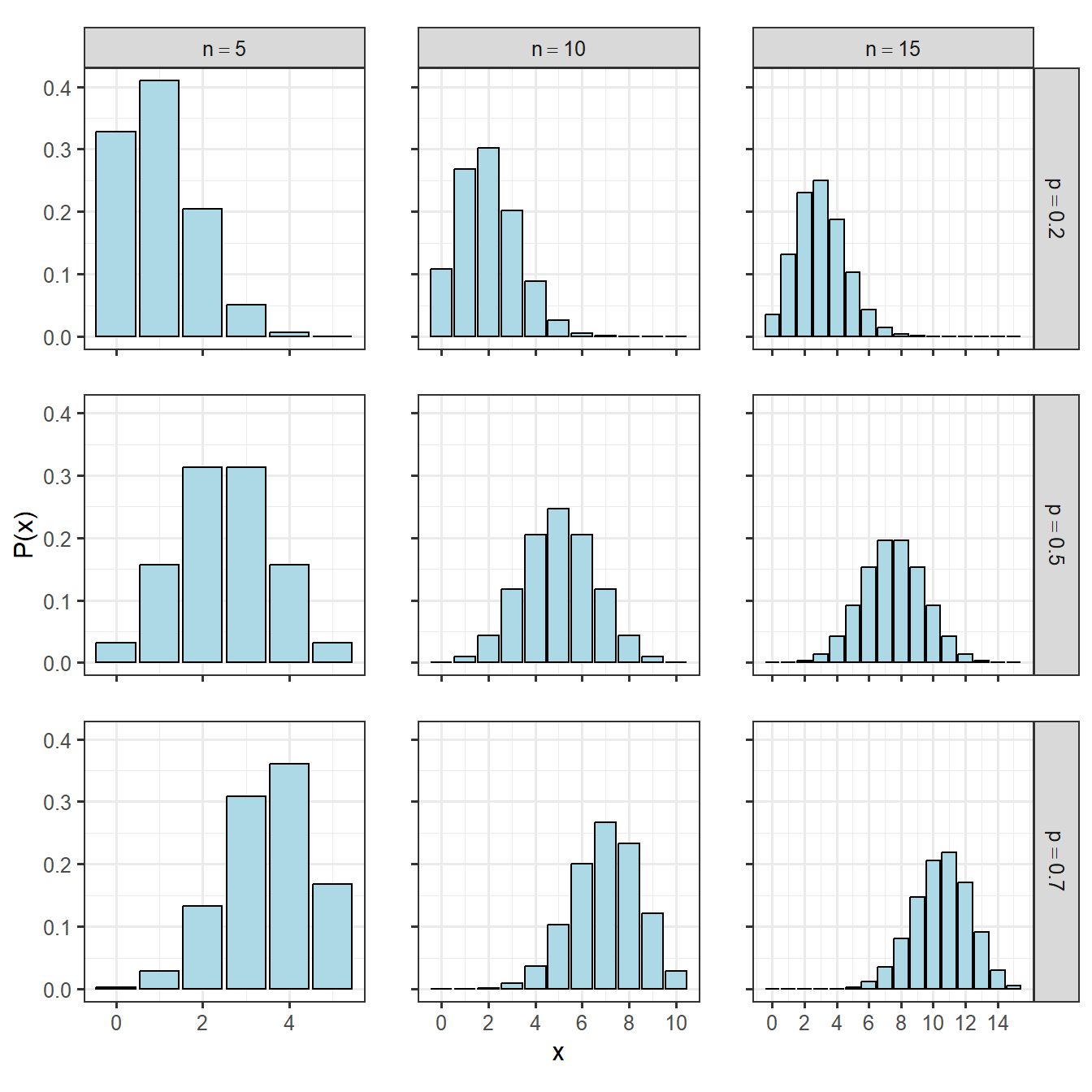
図2.7: 様々な二項分布
2.5.3 ベータ二項分布
ベータ二項分布は、二項分布の期待値\(p\)が共通のベータ分布から得られると仮定する混合分布です。ベータ二項分布は二項分布よりも裾の広い分布をとることができるので、よりばらつきの大きいデータに対して用いることができます。
確率質量関数はベータ分布のパラメータ\(\alpha\)と\(\beta\)、二項分布のパラメータ\(n\)を用いて以下のように書けます。ベータ分布と同様に、\(\theta = \alpha + \beta\)は分布の広さを表します。
\[ P(x) = \begin{pmatrix} n\\x \end{pmatrix} \frac{B(x + \alpha, n - x + \beta)}{B(\alpha,\beta)} \]
ベータ二項分布の期待値と分散は以下のようになります。RでGLMやGLMMを実行するときには、通常平均\(\mu\)と\(\theta\)を用いてモデル化され、推定が行われることが多いです。
- 期待値: \(\mu = \frac{\alpha}{\alpha + \beta}\)
- 分散: \(n\frac{\alpha\beta}{(\alpha + \beta)^2} \frac{\alpha + \beta + n}{\alpha + \beta + 1}\)
\(\mu\)と\(\theta\)の値を変えたときの負の二項分布を描いたのが図(fog:ex-bb)です。 二項分布よりも様々な形をとることができることが分かります。
n <- 10
x <- seq(0,10,1)
mu <- c(0.2,0.5,0.7)
theta <- c(1,4,7)
crossing(x,n, mu, theta) %>%
mutate(prob = dbetabinom(x, size = n, prob = p, theta = theta)) %>%
mutate(mu = str_c("mu == ", mu),
theta = str_c("theta == ", theta)) %>%
ggplot(aes(x = x, y = prob))+
labs(x = "x", y = "P(x)")+
scale_x_continuous(breaks = seq(0,15,2))+
geom_col(fill = "lightblue",
color = "black")+
theme_bw(base_size = 12)+
theme(aspect.ratio = 1)+
facet_rep_grid(theta ~ mu,
labeller = label_parsed,
scales = "free_x")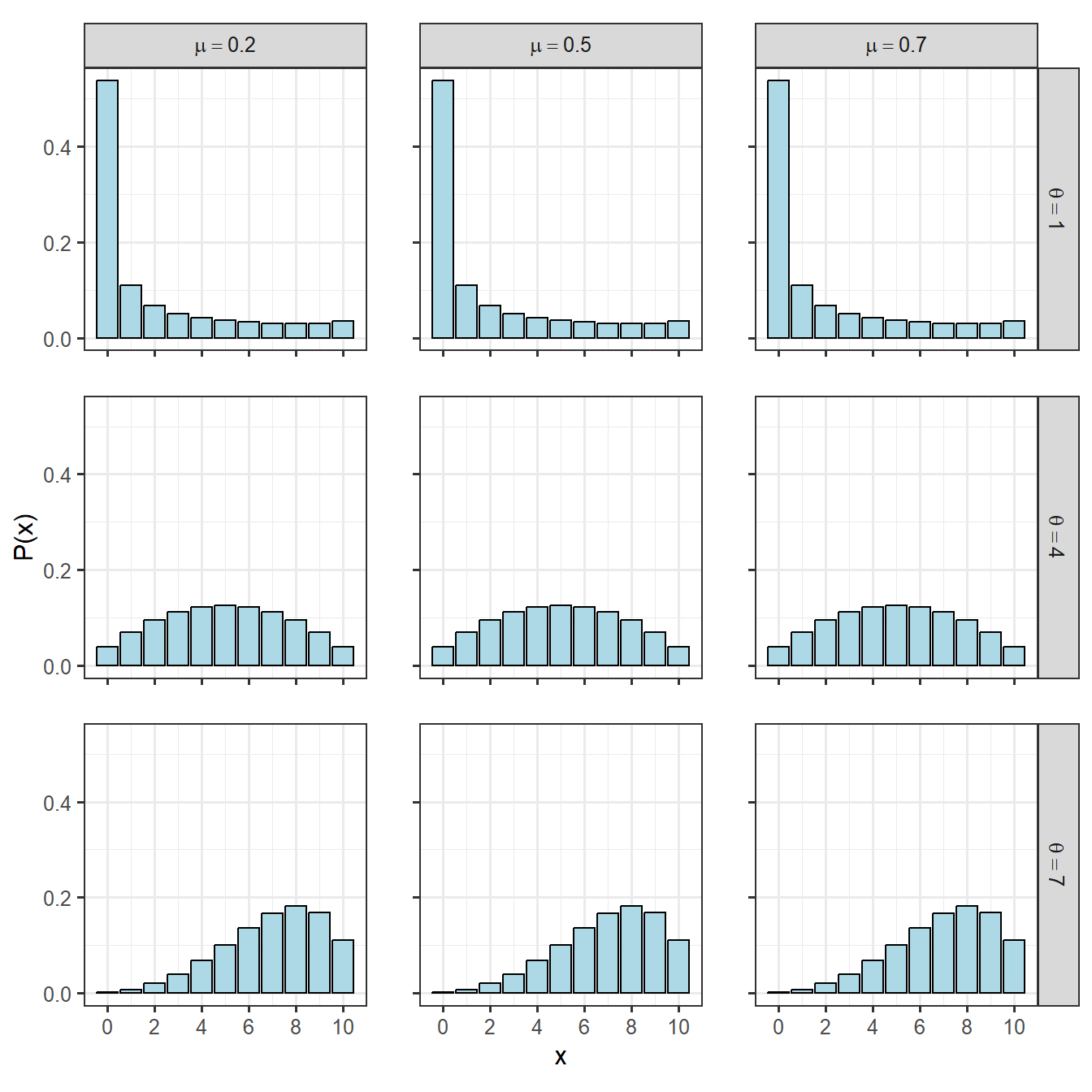
図2.8: 様々なベータ二項分布
2.5.4 ポワソン分布
ポワソン分布は、「ある一定の時間にある事象が発生する回数(\(x\))を表す確率分布」です。たとえば、1年間に自動車事故が発生する回数はポワソン分布に従うとされます。二項分布と違い、ポワソン分布は上限のない整数をとる変数に対して用いることができます。
ある事象が起きる平均回数を\(\lambda\)とするとき、その事象が\(x\)回生じる確率(\(P(x)\))は以下のようになります。これがポワソン分布の確率質量関数です。
\[ P(x) = \frac{\lambda^x}{x!}e^{-\lambda} \quad (x \geq 0) \]
ポワソン分布は期待値も分散も\(\lambda\)になります。様々なポワソン分布を書いてみると以下のようになります(図2.9)。
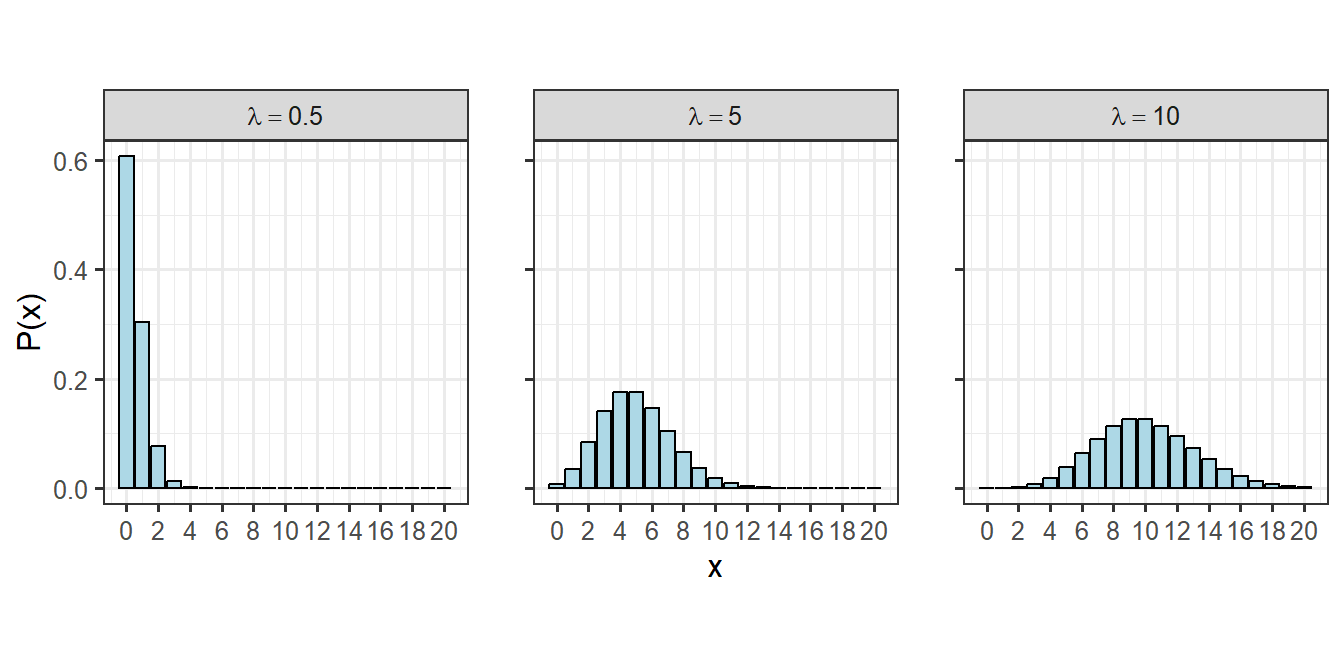
図2.9: 様々なポワソン分布
2.5.5 負の二項分布
負の二項分布は、ポワソン分布のパラメータ\(\lambda\)が共通のガンマ分布から得られるとする混合分布です。先述のようにポワソン分布は期待値も分散も同じ分布ですが、こうすることにより負の二項分布はポワソン分布よりも裾の広い分布をとることができるので、よりばらつきの大きいデータに対して用いることができます。
負の二項分布の確率質量関数はガンマ分布のパラメータ\(\alpha\)と\(\beta\)を用いて以下のように書けます。\(\alpha \rightarrow \infty\)のとき、負の二項分布はポワソン分布になります。
\[ P(x) = \frac{\Gamma(x + \alpha)}{\Gamma(\alpha)x!} \Bigl(\frac{\beta}{1 + \beta}\Bigl)^n\Bigl(\frac{1}{1 + \beta}\Bigl)^x \]
分布の期待値と分散は以下のようになります。RでGLMやGLMMを実行するときには、通常平均\(\mu\)と\(\alpha\)を用いてモデル化され、推定が行われることが多いです。そのとき、\(\alpha\)は分散パラメータ\(\phi\)と呼ばれます。
- 期待値: \(\mu = \alpha/\beta\)
- 分散: \(\mu + \mu^2/\alpha\)
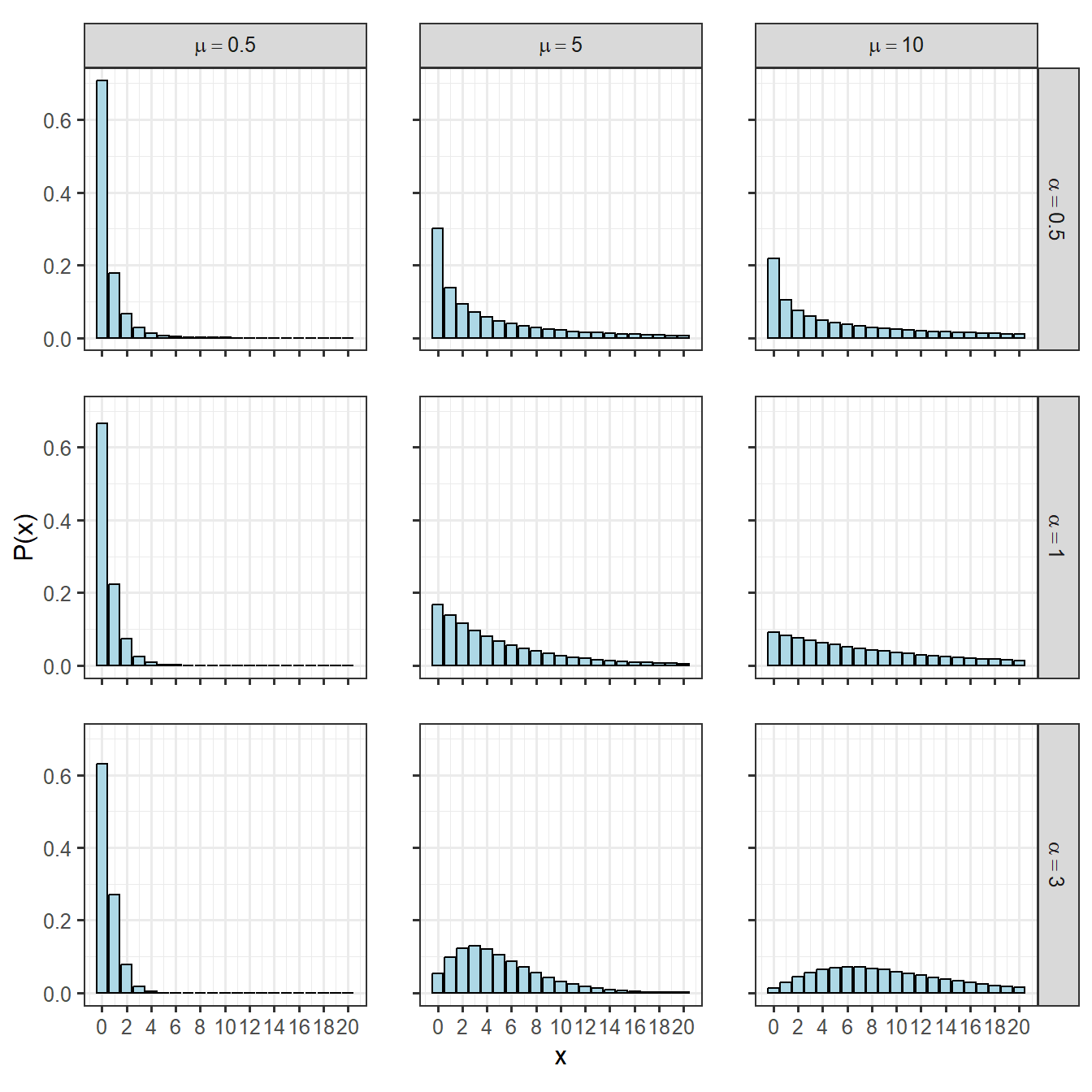
図2.10: 様々な負の二項分布