2. Steepnessの算出

2.1 Steepnessとは

続いて、順位序列のsteepnessを算出する。
steepnessは順位序列の厳しさを表し、例えば専制的な種ほどその値は高くなるとされる(Balasubramaniam et al. 2012)。X軸に順位が高い個体から名前を並べ、Y軸にnDSをプロットするとき、その回帰直線の傾きの絶対値がsteepnessとなる。0から1の値を取り、1に近づくほどsteepnessが高いことを示す。

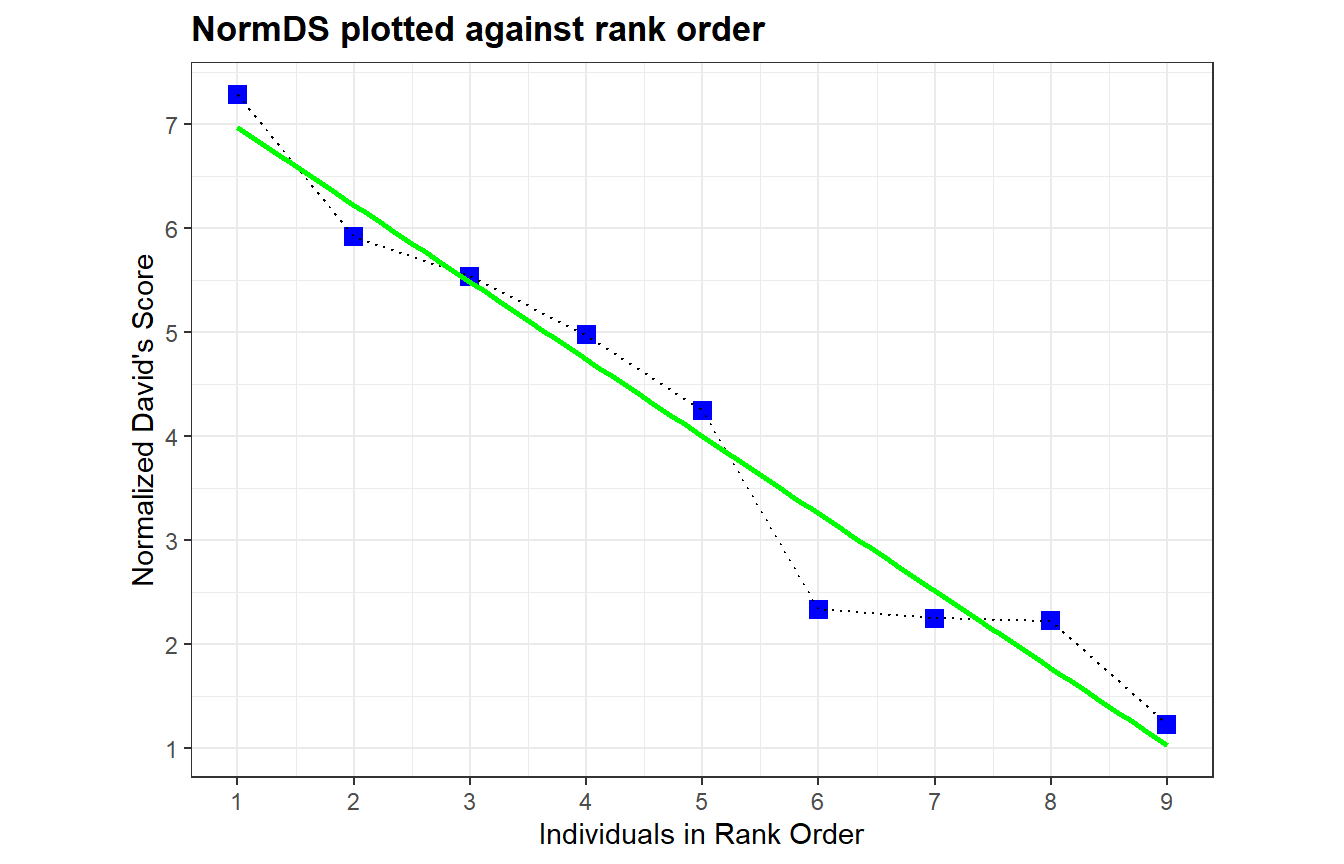
単回帰分析を行ってやれば、steepness(=傾き)は算出できる。 今回の例では、傾きは約0.7421となることがわかる。

## 単回帰分析  
r <- lm(data= nDS_d2, normDS~x)

## 傾きの絶対値    
abs(r$coefficients[[2]])

## [1] 0.7420538

2.2 Rでの算出方法

EloRatingパッケージのsteepness関数を用いることで、回帰分析をしなくてもsteepnessを算出することができる。Dij = TRUEをすると\(D_{ij}\)を用いたnDSを、Dij = FALSEをすると\(P_{ij}\)を用いたnDSを用いてsteepnessを算出する。

stp <- EloRating::steepness(mat, Dij = TRUE)

stp

##     steep  expected         p     nrand 
## 0.7420538        NA        NA 0.0000000

個体の勝敗がランダムに決まるときに比べて、steepnessが有意に高いかを検定することもできる(De Vries et al. 2006)。検定をする場合、ランダム化を行う回数をnrand =で指定する。今回の場合、\(p < 0.001\)となり、有意であることが分かった。

EloRating::steepness(mat, Dij = TRUE, nrand = 10000)

##        steep     expected            p        nrand 
## 7.420538e-01 3.004903e-01 1.000000e-04 1.000000e+04

returnfig = TRUEとすると、ランダムに勝敗が決まる場合のsteepnessの分布(extected)と実際のsteepnessの値(expected)をプロットできる。

EloRating::steepness(mat, Dij = TRUE, nrand = 10000, returnfig = TRUE)

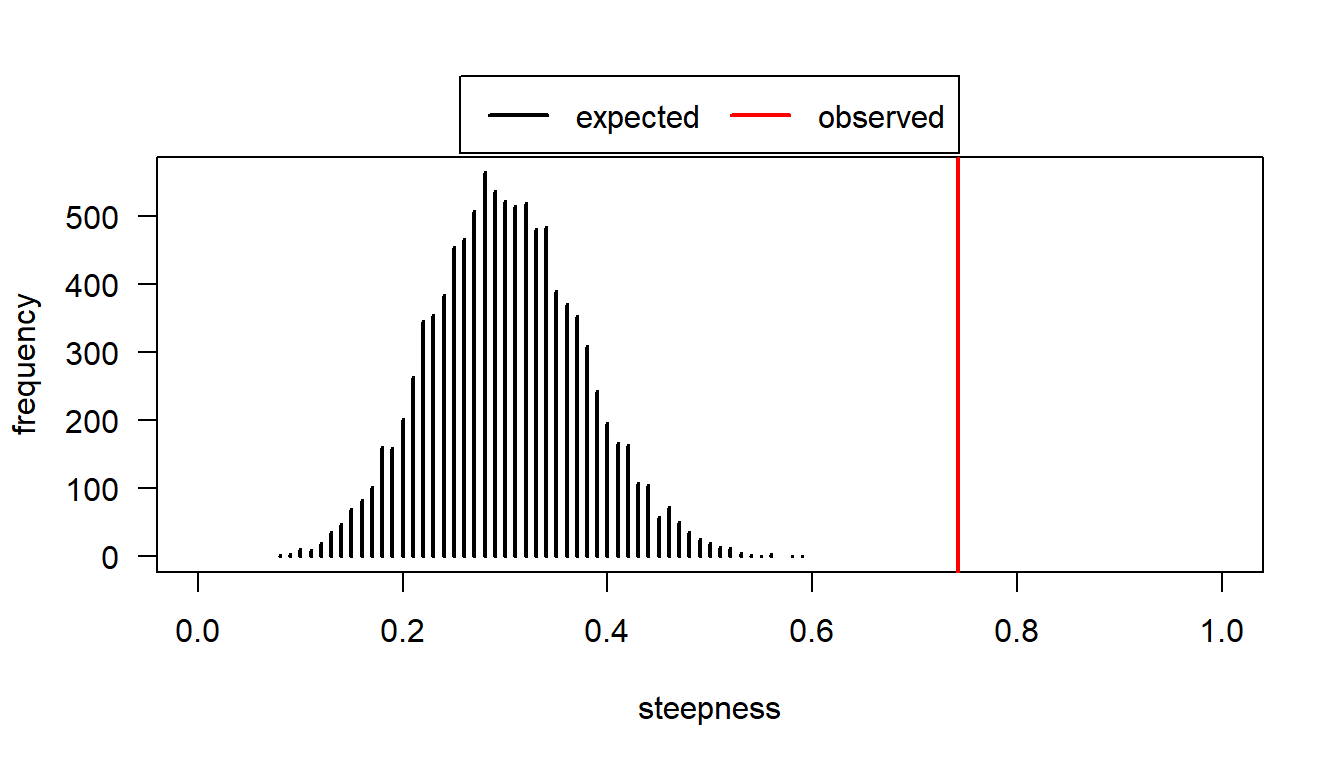
##        steep     expected            p        nrand 
## 7.420538e-01 3.013294e-01 1.000000e-04 1.000000e+04

References

Balasubramaniam KN, Dittmar K, Berman CM, et al (2012) Hierarchical steepness and phylogenetic models: Phylogenetic signals in macaca. Anim Behav 83:1207–1218

De Vries H, Stevens JMG, Vervaecke H (2006) Measuring and testing the steepness of dominance hierarchies. Anim Behav 71:585–592