4. Elo-ratingの算出
4.1 Elo-ratingとは
Elo-ratingとは、各個体の相対的な強さを表す指標であり、そのときどきの勝敗によって常に変動する。主にサッカーやチェス、将棋などの競技で用いられているが、近年霊長類学を含む動物行動学の分野でもよく使われるようになっている(Foerster et al. 2016; Newton-Fisher 2017; Mielke et al. 2019; Ballesta et al. 2021; Neumann and Fischer 2023; Jarvey et al. 2024)。時系列的に指標の変化を調べることができ、交渉結果によって指標が随時更新されていくという点で他の順位関連指標(e.g., David’s score)とは異なる(cf. Albers and Vries 2001)。
Elo-ratingでは、交渉のたびに交渉前のレーティングから予想される勝利確率と実際の交渉結果を比較し、これらがどの程度違うかによってレーティングを更新していく。具体的には、個体\(A\)と\(B\)のレーティングを\(R_A, R_B\)、個体\(A\)が\(B\)に勝つ確率を\(p_{AB}\)とするとき、交渉後のレーティング(\(R_{Anew}, R_{Bnew}\))は以下のように変化する(Neumann et al. 2011)。なお、\(k\)は定数で自由に設定できる。\(k\)が大きいほど1回の交渉がレーティングに与える影響が大きくなる。
Aが勝った場合
\[
R_{Anew} = R_A + (1-p_{AB})\times k\\
R_{Bnew} = R_B - (1-p_{AB})\times k
\]
Bが勝った場合
\[
R_{Anew} = R_A - p_{AB}\times k\\
R_{Bnew} = R_B + p_{AB}\times k
\]
なお、交渉前の勝利確率\(p_{AB}\)は一般に以下の式で計算される(Wikipediaより)。
\[
p_{AB} = \frac{1}{10^{(R_B - R_A)/400} + 1}
\]
ただし、勝利確率をどのように算出するかについては、まだコンセンサスが得られておらず、様々な方法があるようだ(Neumann and Fischer 2023)。霊長類の研究(e.g., Franz et al. 2015; Goffe et al. 2018)では、交渉前に個体\(A\)が\(B\)に勝つ確率\(P_{AB}\)を以下のように定義している。なお、 Franz et al. (2015) では\(\delta = 0.01\)、 Goffe et al. (2018) では\(\delta = 1\)としている。
\[ P_{AB} = \frac{1}{1 + exp(- \delta(R_A - R_B))} \]
4.2 Rを用いた算出と可視化
4.2.1 Elo-ratingの算出
4.2.1.1 交渉の種類を考慮しない場合
EloRatingパッケージでは、以下のような日付と勝敗が示されたデータを用いてElo-ratingを算出する。
Elo-ratingはelo.seq関数を用いて算出できる。winner =に勝者の値をおさめたベクトルを、loser =に敗者の値をおさめたベクトルを、Dateで日付をおさめたベクトルを、k =で\(k\)を指定する。その他の引数については、?elo.seqを参照。
\(k\)の値については、optimizek関数を用いて、実際の交渉データに最もよく符合するような\(k\)を最尤法で推定することもできる1。krange =で想定する\(k\)の範囲を、resolution =で指定した範囲を何等分した値を用いて推定を行うかを指定する。今回の場合は、最尤推定値はk = 252.6982になるようだ(loglikはそのときの対数尤度)。
この値を用いてもう一度Elo-ratingを算出すると以下のようになる。
summary関数で日付の範囲や交渉の数などの基本情報を確認できる。
## Elo ratings from 7 individuals
## total (mean/median) number of interactions: 33 (9.4/9)
## range of interactions: 7 - 11
## date range: 2010-01-01 - 2010-02-02
## startvalue: 1000
## uppon arrival treatment: average
## k: 252.698213964279
## proportion of draws in the data set: 0Elo-ratingの時系列的変化はeloplot関数で以下のように描画できる(図3)。from =とto =で日付の範囲を、ids =で描画したい個体名を指定する。
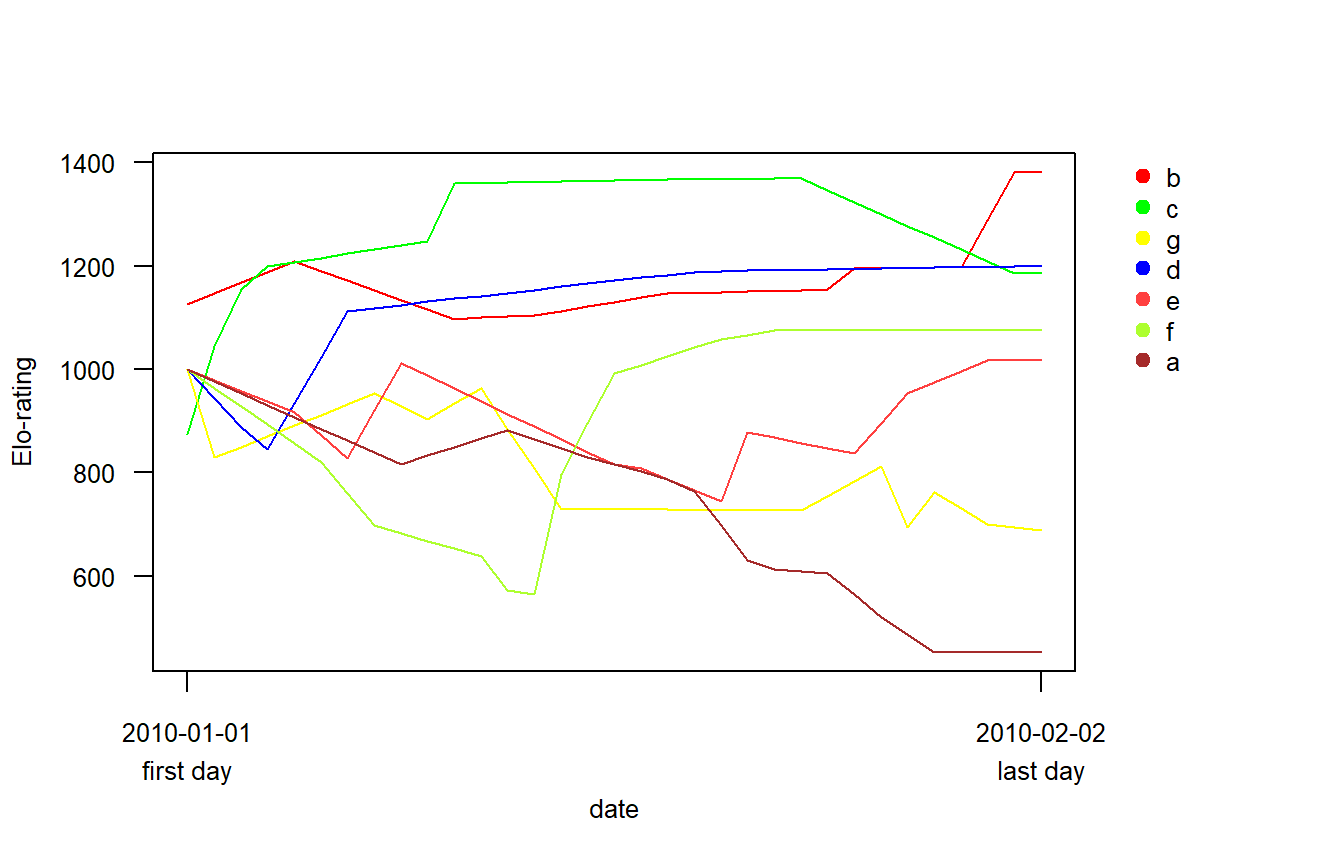
Figure 3: 交渉の種類を考慮しない場合のElo-rating
4.2.1.2 交渉の種類を考慮する場合
交渉の種類が複数あり、それぞれの激しさが異なるようなとき(例えば、サプラント、威嚇、物理的攻撃など)、それぞれについて異なる\(k\)の値を付すこともできる(Newton-Fisher 2017)。例えば、以下のadv2というデータでは、intensity列に各交渉で見られた敵対的交渉が2種類記録されている(displaceかfight)。
displaceなら\(k = 50\)、fightなら\(k = 200\)の様にlist形式でそれぞれの\(k\)を書いたものを、elo.seq関数のk =で指定する。また、intensity =に交渉の種類を示したベクトルを指定する。
myk <- list(displace = 50, fight = 200)
res_int <- elo.seq(winner = adv2$winner, loser = adv2$loser, Date = adv2$Date,
k = myk, intensity = adv2$intensity)この場合も同様に、最尤法を利用して実際の交渉データに最もよく符合するような\(k\)を推定できる。krange =でlist形式でそれぞれの種類ごとに想定する\(k\)の範囲を、itype =でそれぞれの交渉の種類の名前のベクトルを指定する。
今回の場合は、displaceのときは\(k = 186.0861\)、fightのときは\(k = 477.9279\)と推定された。
ml_z2 <- optimizek(res_int,
krange = list(displace = c(10,500), fight = c(10,500)),
resolution = 1000,
itype = adv2$intensity)
ml_z2$best この値を用いてもう一度Elo-ratingを算出すると以下のようになる。
myk2 <- list(displace = ml_z2$best$displace, fight = ml_z2$best$fight)
res_int_opt <- elo.seq(winner = adv2$winner, loser = adv2$loser, Date = adv2$Date,
k = myk2, intensity = adv2$intensity)summary関数で日付の範囲や交渉の数などの基本情報を確認できる。
## Elo ratings from 7 individuals
## total (mean/median) number of interactions: 33 (9.4/9)
## range of interactions: 7 - 11
## date range: 2010-01-01 - 2010-02-02
## startvalue: 1000
## uppon arrival treatment: average
## k: custom values ranging between 186.086086086086 and 477.927927927928
## proportion of draws in the data set: 0Elo-ratingの時系列的変化をeloplot関数で描画すると以下のようになる(図4)。
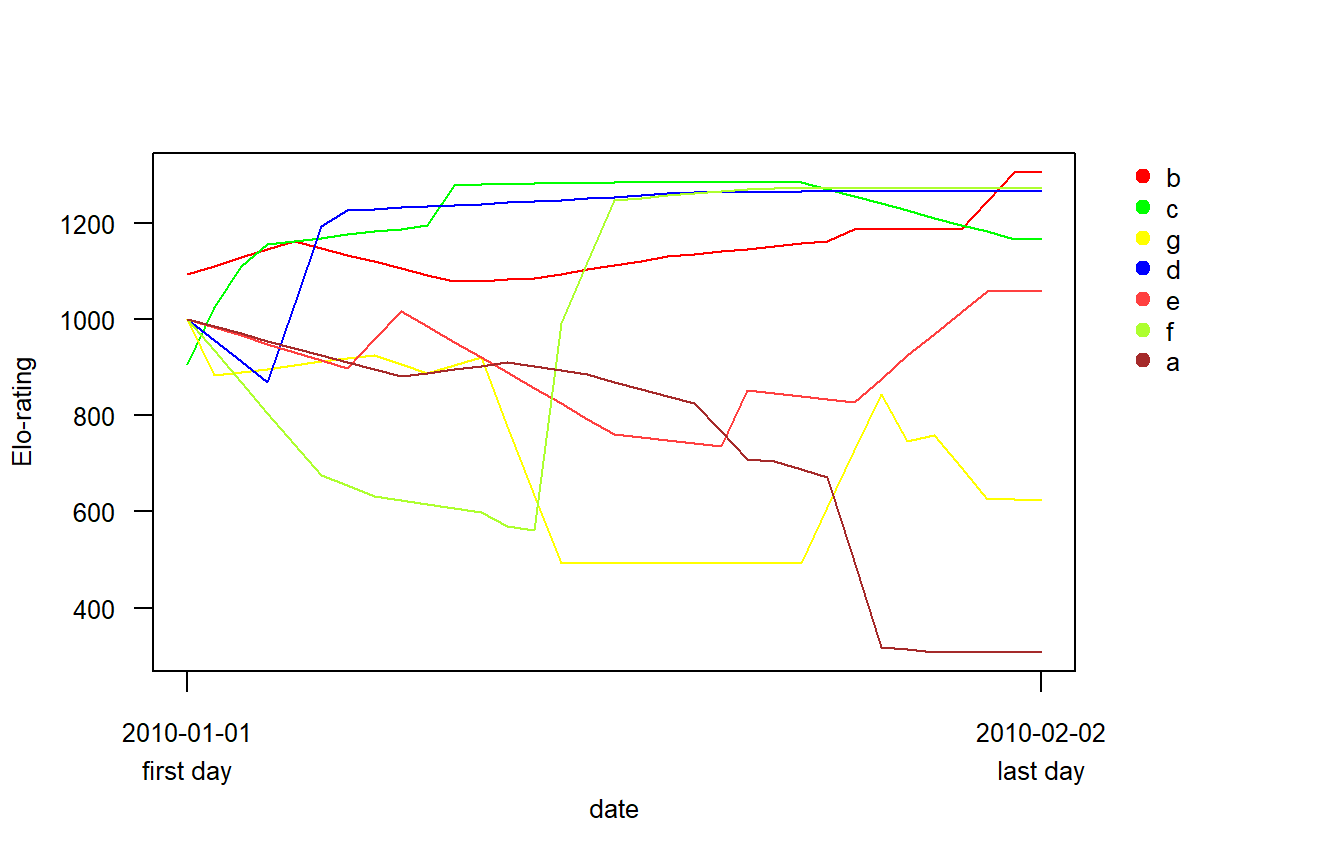
Figure 4: 交渉の種類を考慮した場合のElo-rating
4.2.1.3 事前情報を考慮する場合
Elo-ratingは、データ収集の開始時点では全ての個体のレーティングが等しいと仮定され、それを実際の交渉の結果によって更新していく。しかし、これは集団が新たに形成された場合は適切であるが、集団がデータ収集前から存在している場合には妥当ではない(Newton-Fisher 2017)。また、Elo-ratingが実際の優劣関係と一致するためには、交渉数が十分に蓄積する時点までburn-in期間と呼ばれる期間が必要である(Albers and Vries 2001; Neumann et al. 2011)。この期間のElo-ratingは信頼性が低く、分析などに使用することができない(Newton-Fisher 2017)。
これらの問題を解決するため、 Newton-Fisher (2017) は事前に個体間の優劣関係についてわかっている情報をElo-ratingの算出に用いることを提案している。この方法を用いれば、データ収集の開始時点から個体間のレーティングが全く同じになることはなく、またburn-in期間を短縮できる可能性がある。
事前に個体間の優劣関係(e.g., 順位など)が分かっているとき、開始時点の個体\(i\)のElo-ratingは以下のように定義される(Newton-Fisher 2017)。\(S_e\)は事前の情報がない場合の開始時点のレーティング(デフォルトは1000)、\(x_r\)は事前情報で分かっている全個体の順位の中央値、\(S_{ri}\)は事前情報による個体\(i\)の順位である2。\(k\)は前節までと同じで、\(l_r\)は事前情報による順位をどの程度反映させるかを決める定数で、0から1の値を指定できる。
\[ E_i = S_e + [(x_r - S_{ri})\times k \times S_{ri}^{-l_r}] \]
例えば、事前に順位(1位, 2位, …, 10位)の情報があるとき、\(l_r\)の値による開始時点のレーティングは以下のような関係になる。
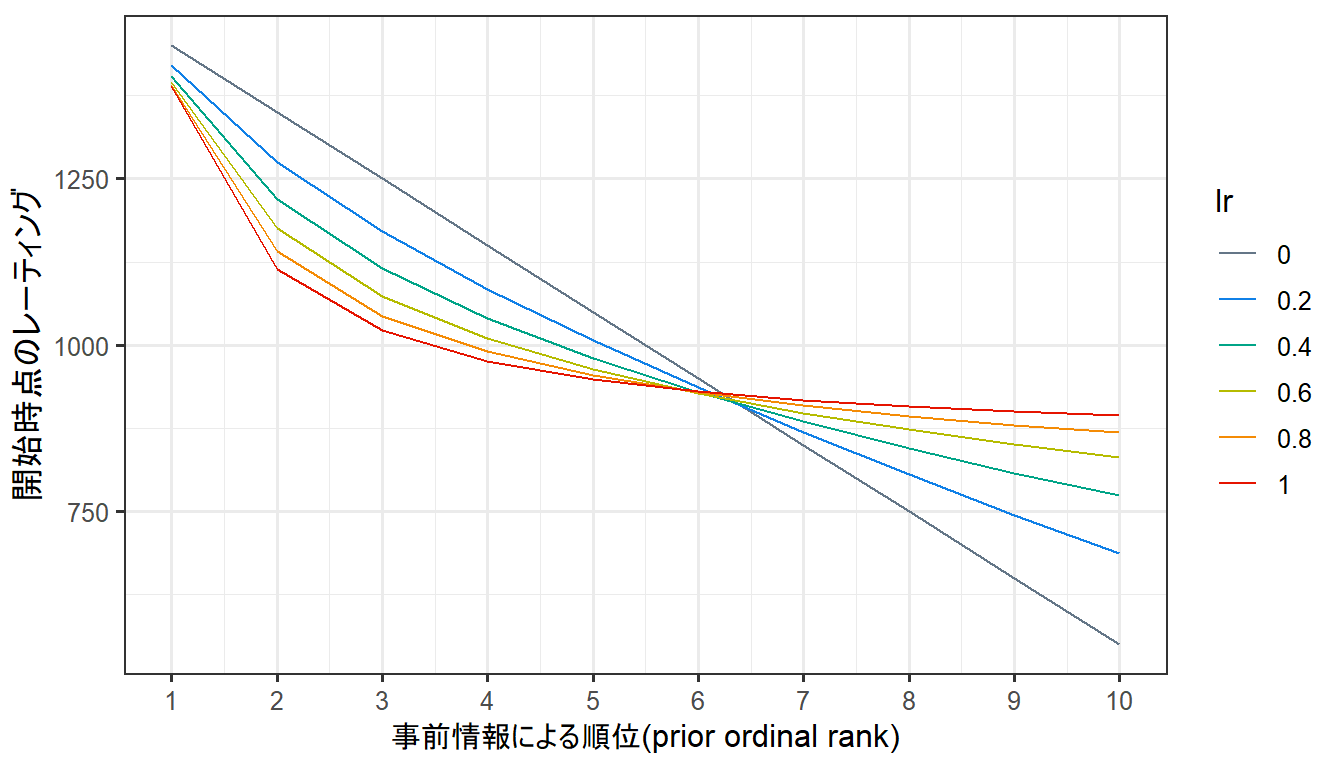
Figure 5: lrによる開始時点のレーティング。
それでは、Rを用いて算出してみよう。以下のように事前に順位(e.g., 1位, 2位, …)が分かっているとする。
## b c d f e g a
## 1 2 3 4 5 6 7このとき、開始時点のレーティングはbreatestartvalues関数で以下のように算出できる。shape =で\(\delta\)を、startvalue =で\(S_e\)を、k =で\(k\)を指定する。
## b c d f e g a
## 1273 1136 1045 973 911 856 806これを事前情報として用いたElo-ratingは以下のように算出する。startvalue =で先ほど算出したレーティングのベクトルを指定する。
res_prior <- elo.seq(winner= adv2$winner, loser= adv2$loser,
Date = adv2$Date, startvalue = mystart$res)Elo-ratingの時系列的変化をeloplot関数で描画すると以下のようになる(図6)。事前情報がなかった場合(図3と図4)に比べてレーティングが安定するのが早く、burn-in期間が短くなっていることが分かる。
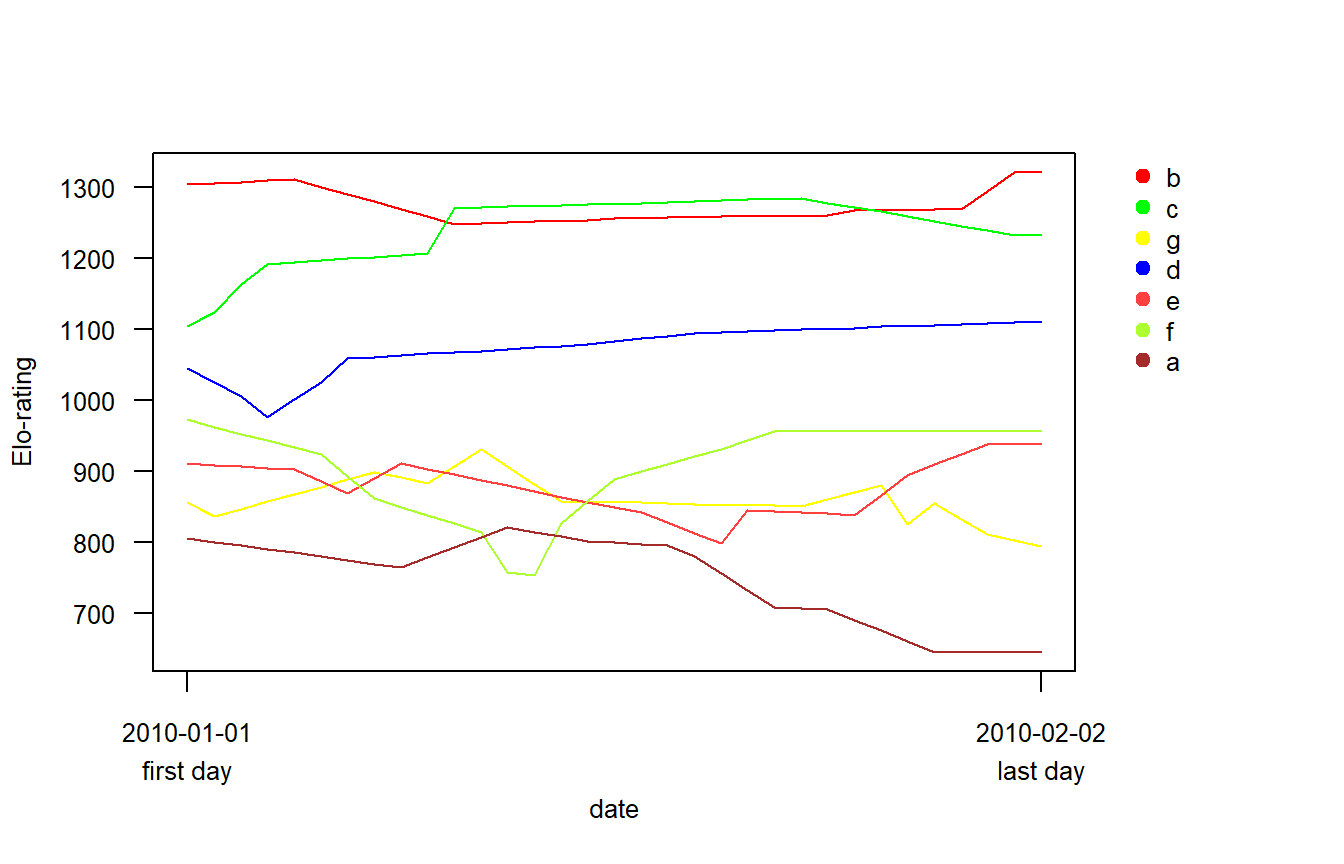
Figure 6: 事前情報(数字の順位)を考慮した場合のElo-rating
順位が以下のようにカテゴリでしかわかっていない場合でも、事前情報を考慮して算出を行うことができる(ただし、現時点では4カテゴリのみ可能)。順位の情報はlist形式で作成する。4カテゴリ未満の場合、使っていないクラスの個体名はNULLとする。
myrank_cat <- list(alpha = "a", high = c("b","c"),
mid = c("d", "e"), low = c("f", "g"))
## 4カテゴリ未満の場合
# myrank_cat <- list(high = c("a","b","c"), mid = NULL,
# low = c("d","e","f","g"), superlow = NULL)
myrank_cat## $alpha
## [1] "a"
##
## $high
## [1] "b" "c"
##
## $mid
## [1] "d" "e"
##
## $low
## [1] "f" "g"このとき、開始時点のレーティングはbreatestartvalues関数で以下のように算出できる。rankclasses =で先ほど作成したlistを指定する。
mystart_cat <- createstartvalues(rankclasses = myrank_cat,
shape = 0.3, startvalue = 1000,
k = 100)
mystart_cat$res## a b c d e f g
## 1202 1100 1100 952 952 846 846これを事前情報として用いたElo-ratingは以下のように算出する。startvalue =で先ほど算出したレーティングのベクトルを指定する。
res_prior_cat <- elo.seq(winner= adv2$winner, loser= adv2$loser,
Date = adv2$Date, startvalue = mystart_cat$res)Elo-ratingの時系列的変化をeloplot関数で描画すると以下のようになる(図7)。やはり事前情報がなかった場合(図3と図4)に比べてレーティングが安定するのが早く、burn-in期間が短くなっていることが分かる。
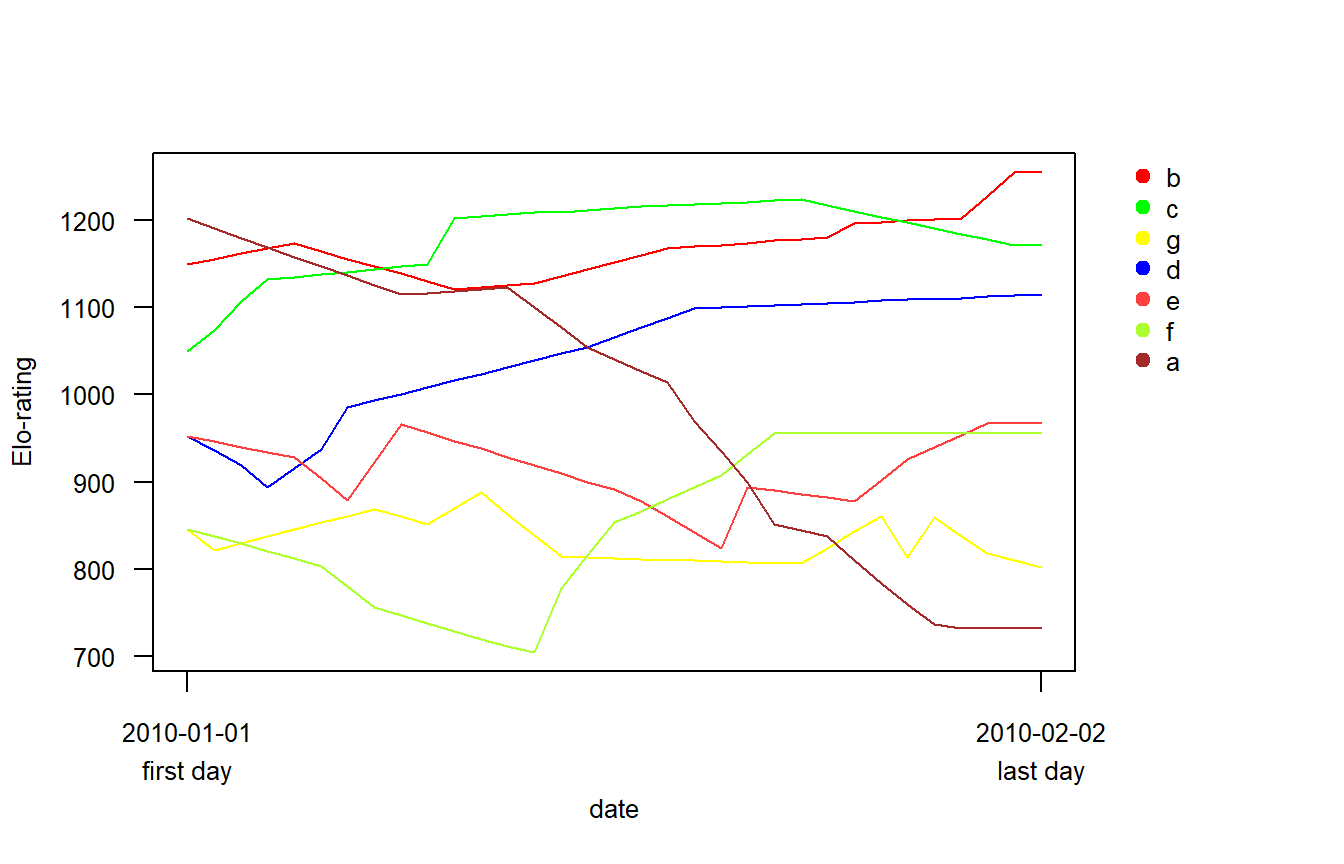
Figure 7: 事前情報(順位カテゴリ)を考慮した場合のElo-rating
4.2.2 Elo-ratingの抽出
ある日付におけるElo-ratingはextract_elo関数で以下のように求められる。extractdate =で日付を、IDs =で値を求めたい個体名を指定する(指定しなければ全個体について出力する)。
## d b g
## 1265 1187 747日付を指定しなければ最終日のElo-ratingが求められる。
## b f d c e g a
## 1305 1272 1267 1167 1058 624 307複数の日のデータを一度に取得したい場合は、extradate =で日付を表すベクトルを、IDs =で個体名を表すベクトルを指定する。例えば、元データadvに勝者(winner)と
敗者(loser)のElo-ratingを示す列を作成する場合は以下のようにする。
adv %>%
## 勝者のElo-rating
mutate(Rate_winner = extract_elo(res_int_opt,
extractdate = adv2$Date,
IDs = adv2$winner)) %>%
## 敗者のElo-rating
mutate(Rate_loser = extract_elo(res_int_opt,
extractdate = adv2$Date,
IDs = adv2$loser)) 新しく日付と個体名を含むデータフレームを作成し、そこに各個体のElo-ratingを表す列を作成するというようなこともできる。
## 全ての日付と個体名の組み合わせを含むデータフレームを作成
all_combi <- crossing(Date = unique(adv2$Date),
ID = unique(c(adv2$winner, adv2$loser)))
## 各日・各個体のElo-ratingを算出
all_combi %>%
mutate(Elo_rating = extract_elo(res_int_opt,
extractdate = all_combi$Date,
IDs = all_combi$ID)) References
\(k\)の推定方法には、
optim関数を用いた最尤推定を行う方法(Foerster et al. 2016)、ベイズ推定を行う方法や(Goffe et al. 2018; Neumann and Fischer 2023)、\(k\)を応答変数、多数の変数を説明変数とした一般化線形モデルによって最尤推定されたパラメータによる予測値を用いる方法(Franz et al. 2015)など、他にも様々なものがあるようだ。ただし、いずれもEloRatingパッケージには実装されていない。↩︎数字の順位(1位, 2位, …, 10位)が分かっている場合はそれをそのまま使用する。順位がカテゴリカルな場合も使えるが、現在は4カテゴリの場合のみ使用できる。このとき、順位が高いカテゴリから順に\(1, N/4, N/2, N - N/4\)が割り当てられて使用される(\(N\)は個体数)。↩︎